Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T18:26:47.496Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of pitch rate on freely translating perching airfoils

Published online by Cambridge University Press:  20 June 2019

T. Jardin Open the ORCID record for T. Jardin [Opens in a new window]  and
N. Doué
T. Jardin*
Affiliation:
ISAE-SUPAERO, Université de Toulouse, 31055 Toulouse CEDEX 4, France
N. Doué
Affiliation:
ISAE-SUPAERO, Université de Toulouse, 31055 Toulouse CEDEX 4, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We numerically investigated the unsteady dynamics of a two-dimensional airfoil undergoing a continuous, prescribed pitch-up motion and freely translating as a response to aerodynamic forces and the gravity field. The pitch-up motion was applied about an axis located 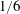$1/6$ chord away from the leading edge and was parameterized using the shape change number, with a Reynolds number set to 2000. It was shown that the minimum kinetic energy reached by the airfoil depends stochastically and asymptotically on shape change numbers for values below and above 1, respectively. Very low kinetic energy levels (close to zero) can be reached in both stochastic and asymptotic regions but high shape change numbers are accompanied by significant gain in altitude which may be undesirable from a practical perspective. Rather, shape change numbers in the range [0.1–0.3] allow us to reach relatively low levels of kinetic energy for close perching locations. We showed that highly nonlinear fluid–structure interactions induced by massive flow separations and strong vortices are conducive to low kinetic energy, but responsible for the stochastic dependence of kinetic energy to shape change number, which can make perching manoeuvres hardly controllable for flying vehicles.

JFM classification

Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 49 - 71
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berg, A. M. & Biewener, A. A. 2010 Wing and body kinematics of takeoff and landing flight in the pigeon (Columbia livia). J. Expl Biol. 213, 1651–1658.Google Scholar
Carruthers, A. C., Thomas, A. L. R. & Taylor, G. K. 2007 Automatic aeroelastic devices in the wings of a steppe eagle aquila nipalensis. J. Expl Biol. 210, 4136–4149.Google Scholar
Carruthers, A. C., Thomas, A. L. R., Walkers, S. M. & Taylor, G. K. 2010 Mechanics and aerodynamics of perching manoeuvres in a large bird of prey. Aeronaut. J. 114, 673–680.Google Scholar
Chang, C. C. 1992 Potential flow and forces for incompressible viscous flow. Proc. R. Soc. Lond. A 437, 517–525.Google Scholar
Demirdžić, I. & Muzaferija, S. 1995 Numerical method for coupled fluid flow, heat transfer and stress analysis using unstructured moving meshes with cells of arbitrary topology. Comput. Meth. Appl. Mech. Engng 125, 235–255.Google Scholar
Eldredge, J. D. & Jones, A. R. 2019 Leading-edge vortices: mechanics and modeling. Annu. Rev. Fluid Mech. 51, 75–104.Google Scholar
Eldredge, J. D. & Wang, C. 2010 High-fidelity simulations and low-order modeling of a rapidly pitching plate. In 40th AIAA Fluid Dynamics Conference and Exhibit, Chicago, Illinois, USA, pp. 2010–4281. American Institute of Aeronautics and Astronautics.Google Scholar
Fernando, J. N. & Rival, D. E. 2017 On the dynamics of perching manoeuvres with low-aspect-ratio planforms. Bioinspir. Biomim. 12, 046007.Google Scholar
Ford, C. P. & Babinsky, H. 2013 Lift and the leading edge vortex. J. Fluid Mech. 720, 280–313.Google Scholar
Granlund, K. O., Ol, M. V. & Bernal, L. P. 2013 Unsteady pitching flat plates. J. Fluid Mech. 733, R5.Google Scholar
Grasmeyer, J. M. & Keennon, M. T. 2001 Development of the black widow micro air vehicle. AIAA J. 748, 932–956.Google Scholar
Hunt, J. C. R., Wray, A. & Moin, P.1988 Eddies, stream, and convergence zones in turbulent flows, Center for Turbulence Research Report (CTR-S88).Google Scholar
Jardin, T. & Colonius, T. 2018 On the lift-optimal aspect ratio of a revolving wing at low Reynolds number. J. R. Soc. Interface 15 (143), 20170933.Google Scholar
Kramer, M. 1932 Die Zunahme des Maximalauftriebes von Tragflugeln bei plotzlicher Anstellwinkelvergrosserung (Boeneffekt). Z. Flugtech. Motorluftschiff. 23, 185–189.Google Scholar
Kurtulus, D. F. 2015 On the unsteady behavior of the flow around NACA 0012 airfoil with steady external conditions at Re = 1000. Intl J. Micro Air Veh. 7, 301–326.Google Scholar
McCroskey, W. 1982 Unsteady airfoils. Annu. Rev. Fluid Mech. 14, 285–311.Google Scholar
Moriche, M., Flores, O. & Garcia-Villalba, M. 2017 On the aerodynamic forces on heaving and pitching airfoils at low Reynolds number. J. Fluid Mech. 828, 395–423.Google Scholar
Muzaferija, S.1994 Adaptive finite volume method for flow prediction using unstructured meshes and multigrid approach. PhD thesis, The Imperial College of Science, Technology and Medicine.Google Scholar
Ol, M., Altman, A., Eldredge, J., Garmann, D. & Lian, Y. 2010 Resume of the AIAA FDTC low Reynolds number discussion group’s canonical cases. In 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition 4 – 7 January 2010, Orlando, Florida, p. 1085.Google Scholar
Polet, D. T. & Rival, D. E. 2015 Rapid area change in pitch-up manoeuvres of small perching birds. Bioinspir. Biomim. 10, 066004.Google Scholar
Polet, D. T., Rival, D. E. & Weymouth, G. D. 2015 Unsteady dynamics of rapid perching manoeuvres. J. Fluid Mech. 767, 323–341.Google Scholar
Provini, P., Tobalske, B. W., Crandell, K. E. & Abourachid, A. 2014 Transition from wing to leg forces during landing in birds. J. Expl Biol. 217, 2659–2666.Google Scholar
Visbal, M. R. & Shang, J. S. 1989 Investigation of the flow structure around a rapidly pitching airfoil. AIAA J. 27, 1044–1051.Google Scholar
Widmann, A. & Tropea, C. 2015 Parameters influencing vortex growth and detachment on unsteady aerodynamic profiles. J. Fluid Mech. 773, 432–459.Google Scholar
Wood, R. J. 2008 The first takeoff of a biologically inspired at-scale robotic insect. Robotics, IEEE Transactions on 24, 341–347.Google Scholar
Yu, H. T. & Bernal, L. P. 2016 Effects of pivot location and reduced pitch rate on pitching rectangular flat plates. AIAA J. 55, 702–718.Google Scholar