Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-09T21:50:20.184Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of low-frequency vibration on thermocapillary instability in a binary mixture with the Soret effect: long-wave versus short-wave perturbations

Published online by Cambridge University Press:  02 January 2013

Irina S. Fayzrakhmanova ,
Sergey Shklyaev  and
Alexander A. Nepomnyashchy
Irina S. Fayzrakhmanova
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel Department of General Physics, Perm State Technical University, Perm 614990, Russia Institute of Continuous Media Mechanics, Ural Branch of Russian Academy of Sciences, Perm 614013, Russia
Sergey Shklyaev*
Affiliation:
Institute of Continuous Media Mechanics, Ural Branch of Russian Academy of Sciences, Perm 614013, Russia Department of Chemical Engineering, University of Puerto Rico – Mayagüez, Mayagüez, PR 00681, USA
Alexander A. Nepomnyashchy
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel Minerva Center for Nonlinear Physics of Complex Systems, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the influence of low-frequency vibration on Marangoni instability in a layer of a binary mixture with the Soret effect. A linear stability analysis is performed numerically for perturbations of a finite wavelength (short-wave perturbations). Competition between long-wave and short-wave modes is found: the former ones are critical at smaller absolute values of the Soret number 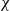$\chi $, whereas the latter ones lead to instability at higher 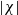$\vert \chi \vert $. In both cases the vibration destabilizes the layer. Two variants of calculations are performed: via Floquet theory (linear asymptotic stability) and taking noise into consideration (empirical criterion). It is found that fluctuations substantially reduce the domains of stability. Further, while studying a limiting case within the empirical criterion, we have found a short-wave instability mode overlooked in former investigations of coupled Rayleigh–Marangoni convection in a layer of pure liquid.

JFM classification

Convection: Marangoni convection Instability: Parametric instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 714 , 10 January 2013 , pp. 190 - 212
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergeon, A., Henry, D. & Ben Hadid, H. 1995 Analytical linear stability analysis of Marangoni instability with Soret effect. Microgravity Q. 5, 123–129.Google Scholar
Bestehorn, M. & Borcia, I. D. 2010 Thin film lubrication dynamics of a binary mixture: example of an oscillatory instability. Phys. Fluids 22, 104102.Google Scholar
Chary, M.-I. & Chen, C.-C. 1997 Onset of stationary Bénard–Marangoni convection in a fluid layer with variable surface tension and viscosity. J. Phys. D 30, 3286–3295.Google Scholar
Fayzrakhmanova, I. S., Shklyaev, S. & Nepomnyashchy, A. A. 2010 Influence of a low frequency vibration on a long-wave Marangoni instability in a binary mixture with the Soret effect. Phys. Fluids 22, 104101.Google Scholar
Fayzrakhmanova, I. S., Shklyaev, S. & Nepomnyashchy, A. A. 2011 Longwave Marangoni instability in a binary mixture under the action of vibration: influence of the heat transfer on a free surface. Eur. Phys. J. Special Topics 192, 95–100.Google Scholar
Finucane, R. G. & Kelly, R. E. 1976 Onset of instability in a fluid layer heated sinusoidally from below. Intl J. Heat Mass Transfer 19, 71–85.Google Scholar
Gershuni, G. Z. & Lyubimov, D. V. 1998 Thermal Vibrational Convection. Wiley.Google Scholar
Homsy, G. M. 1974 Global stability of time-dependent flows. Part 2. Modulated fluid layers. J. Fluid Mech. 62, 387–403.Google Scholar
Lyubimov, D. V., Lyubimova, T. P. & Maryshev, B. S. 2010 Noise effect on convection generation in a modulated gravity field. Fluid Dyn. 45, 859–865.Google Scholar
Lyubimova, T. P. & Parshakova, Y. N. 2007 Stability of equilibrium of a double-layer system with a deformable interface and a prescribed heat flux on the external boundaries. Fluid Dyn. 42, 695–703.Google Scholar
Myznikova, B. I. & Smorodin, B. L. 2001 Convective instability of a horizontal binary-mixture layer in a modulated external force field. Fluid Dyn. 36, 1–19.Google Scholar
Myznikova, B. I. & Smorodin, B. L. 2009 Longwave instability of a binary mixture flow in a vertical channel in the presence of vibration. Fluid Dyn. 44, 240–249.Google Scholar
Nayfeh, A. H. 1973 Perturbation Methods. Wiley.Google Scholar
Nepomnyashchy, A. A. & Simanovskii, I. B. 2007 Marangoni instability in ultrathin two-layer films. Phys. Fluids 19, 122103.Google Scholar
Nield, D. A. 1964 Surface tension and buoyancy effects in cellular convection. J. Fluid Mech. 19, 341–352.Google Scholar
Nield, D. A. 1977 Onset of convection in a fluid layer overlying a layer of a porous medium. J. Fluid Mech. 81, 513–522.Google Scholar
Or, A. C. 2001 Onset condition of modulated Rayleigh–Bénard convection at low frequency. Phys. Rev. E 64, 050201(R).CrossRefGoogle ScholarPubMed
Oron, A. & Nepomnyashchy, A. A. 2004 Long-wavelength thermocapillary instability with the Soret effect. Phys. Rev. E 69, 016313.Google Scholar
Oron, A. & Rosenau, P. 1989 Evolution of the coupled Bénard–Marangoni convection. Phys. Rev. A 39, 2063–2069.CrossRefGoogle ScholarPubMed
Pismen, L. 1988 Selection of long-scale oscillatory convective patterns. Phys. Rev. A 38, 2564–2572.Google Scholar
Podolny, A., Oron, A. & Nepomnyashchy, A. A. 2005 Long-wave Marangoni instability in a binary-liquid layer with deformable interface in the presence of Soret effect: linear theory. Phys. Fluids 17, 104104.Google Scholar
Podolny, A., Oron, A. & Nepomnyashchy, A. A. 2006 Linear and nonlinear theory of longwave Marangoni instability with the Soret effect at finite Biot numbers. Phys. Fluids 18, 054104.Google Scholar
Podolny, A., Nepomnyashchy, A. A. & Oron, A. 2008 Long-wave coupled Marangoni–Rayleigh instability in a binary liquid layer in the presence of the Soret effect. Math. Model. Nat. Phenom. 3, 1–26.Google Scholar
Podolny, A., Nepomnyashchy, A. A. & Oron, A. 2010 Rayleigh–Marangoni instability of binary fluids with small Lewis number and nano-fluids in the presence of the Soret effect. Fluid Dyn. Mater. Process. 6, 13–39.Google Scholar
Rabinovich, M. I. & Trubetskov, D. I. 1989 Oscillations and Waves. Springer.Google Scholar
Rosenblat, S. & Herbert, D. M. 1970 Low-frequency modulation of thermal instability. J. Fluid Mech. 43, 385–398.Google Scholar
Shklyaev, S., Khenner, M. & Alabuzhev, A. A. 2010 Oscillatory and monotonic modes of long-wave Marangoni convection in a thin film. Phys. Rev. E 82, 025302(R).Google Scholar
Shklyaev, S., Khenner, M. & Alabuzhev, A. A. 2012 Long-wave Marangoni convection in a thin film heated from below. Phys. Rev. E 85, 016328.Google Scholar
Shklyaev, S., Nepomnyashchy, A. A. & Oron, A. 2009 Marangoni convection in a binary liquid layer with Soret effect at small Lewis number: linear stability analysis. Phys. Fluids 21, 054101.Google Scholar
Smorodin, B. L., Myznikova, B. I. & Keller, I. O. 2002 On the Soret-driven thermosolutal convection in a vibrational field of arbitrary frequency. Lect. Notes Phys. 584, 372–388.Google Scholar