Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T11:05:19.108Z Has data issue: false hasContentIssue false
  • English
  • Français

The influence of dielectric decrement on electrokinetics

Published online by Cambridge University Press:  29 April 2013

Hui Zhao  and
Shengjie Zhai
Hui Zhao*
Affiliation:
Department of Mechanical Engineering, University of Nevada, Las Vegas, NV 89154, USA
Shengjie Zhai
Affiliation:
Department of Mechanical Engineering, University of Nevada, Las Vegas, NV 89154, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We treat the dielectric decrement induced by excess ion polarization as a source of ion specificity and explore its impact on electrokinetics. We employ a modified Poisson–Nernst–Planck (PNP) model accounting for the dielectric decrement. The dielectric decrement is determined by the excess-ion-polarization parameter $\alpha $ and when $\alpha = 0$ the standard PNP model is recovered. Our model shows that ions saturate at large zeta potentials 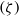$(\zeta )$. Because of ion saturation, a condensed counterion layer forms adjacent to the charged surface, introducing a new length scale, the thickness of the condensed layer 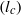$({l}_{c} )$. For the electro-osmotic mobility, the dielectric decrement weakens the electro-osmotic flow owing to the decrease of the dielectric permittivity. At large 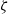$\zeta $, when 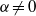$\alpha \not = 0$, the electro-osmotic mobility is found to be proportional to 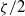$\zeta / 2$, in contrast to 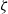$\zeta $ as predicted by the standard PNP model. This is attributed to ion saturation at large 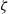$\zeta $. In terms of the electrophoretic mobility ${M}_{e} $, we carry out both an asymptotic analysis in the thin-double-layer limit and solve the full modified PNP model to compute 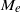${M}_{e} $. Our analysis reveals that the impact of the dielectric decrement is intriguing. At small and moderate 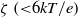$\zeta ~({\lt }6kT/ e)$, the dielectric decrement decreases 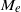${M}_{e} $ with increasing $\alpha $. 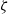At large $\zeta $, it is known that the surface conduction becomes significant and plays an important role in determining 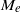${M}_{e} $. It is observed that the dielectric decrement effectively reduces the surface conduction. Hence in stark contrast, 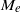${M}_{e} $ increases as $\alpha $ increases. Our predictions of the contrast dependence of the mobility on $\alpha $ at different zeta potentials qualitatively agree with experimental results on the dependence of the mobility among ions and provide a possible explanation for such ion specificity. Finally, the comparisons between the thin-double-layer asymptotic analysis and the full simulations of the modified PNP model suggest that at large 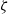$\zeta $ the validity of the thin-double-layer approximation is determined by ${l}_{c} $ rather than the traditional Debye length.

JFM classification

Complex Fluids: Colloids Micro-/Nano-fluid dynamics: Microfluidics Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 724 , 10 June 2013 , pp. 69 - 94
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 21, 61–99.Google Scholar
Anderson, M. B., van Soestbergen, M., Mani, A., Bruus, H., Biesheuvel, P. M. & Bazant, M. Z. 2012 Current-induced membrane discharge. Phys. Rev. Lett. 109, 108301.Google Scholar
Attard, P. 1996 Electrolytes and the electrical double layer. Adv. Chem. Phys. 92, 1–159.Google Scholar
Bazant, M. Z., Kilic, M. S., Storey, B. D. & Ajdari, A. 2009 Towards an understanding of nonlinear electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 152, 48–88.Google Scholar
Bazant, M. Z., Storey, B. D. & Kornyshev, A. A. 2011 Double layer in ionic liquids: overscreening versus crowding. Phys. Rev. Lett 106, 046102.CrossRefGoogle ScholarPubMed
Ben-Yaakov, D., Andelman, D., Harries, D. & Podgornik, R. 2009a Ions in mixed dielectric solvents: Density profiles and osmotic pressure between charged interfaces. J. Phys. Chem. B 113, 6001–6011.Google Scholar
Ben-Yaakov, D., Andelman, D., Harries, D. & Podgornik, R. 2009b Beyond standard Poisson–Boltzmann theory: ion-specific interactions in aqueous solutions. J. Phys.: Condens. Matter 21, 424106.Google ScholarPubMed
Ben-Yaakov, D., Andelman, d. & Podgornik, R. 2011 Dielectric decrement as a source of ion-specific effects. J. Chem. Phys. 134, 074705.CrossRefGoogle ScholarPubMed
Bikerman, J. J. 1942 Structure and capacity of the electric double layer. Phil. Mag. 33, 384–397.Google Scholar
Booth, F. 1951 The dielectric constant of water and the saturation effect. J. Chem. Phys. 19, 391–394.CrossRefGoogle Scholar
Borukhov, I., Andelman, D. & Orland, H. 1997 Steric effects in electrolytes: a modified Poisson–Boltzmann equation. Phys. Rev. Lett. 79, 435–438.Google Scholar
Bostrom, M., Williams, D. R. M. & Ninham, B. W. 2001 Specific ion effects: why DLVO theory fails for biology and colloid systems. Phys. Rev. Lett. 87, 168103.Google Scholar
Buchner, R., Hefter, G. T. & May, P. M. 1999 Dielectric relaxation of aqueous NaCl solutions. J. Phys. Chem. A 103, 1–9.Google Scholar
Cacace, M. G., Landau, E. M. & Ramsden, J. J. 1997 The Hofmeister series: salt and solvent effects on interfacial phenomena. Q. Rev. Biophys. 30, 241–277.Google Scholar
Chandra, A. 2000 Static dielectric constant of aqueous electrolyte solutions: is there any dynamic contribution?. J. Chem. Phys. 113, 903–905.Google Scholar
Collins, K. D. & Washabaugh, M. W. 1985 The Hofmeister effect and the behaviour of water at interfaces. Q. Rev. Biophys. 18, 323–422.Google Scholar
Conway, B. E. 1995 The solvation factor in specificity of ion adsorption at electrodes. Electrochim. Acta 40, 1501–1512.Google Scholar
Danielewicz-Ferchmin, I. & Ferchmin, A. R. 2002 A phase transition in ${\mathrm{H} }_{2} \mathrm{O} $ due to a high electric field close to an electrode. Chem. Phys. Lett. 351, 397–402.Google Scholar
Dukhin, S. S. & Deryaguin, B. V. 1974 Electrokinetic phenomena. In Surface and Colloid Science (ed. Matijevic, E.). vol. 7. Wiley.Google Scholar
Gallardo, V., Salcedo, J., Vera, P. & Delgado, A. V. 1993 Electric and adsorption properties of pharmaceutical polymers. Part I: electrokinetics of aquacoat. Colloid Polym. Sci. 271, 967–973.CrossRefGoogle Scholar
Gavish, N. & Promislow, K. 2012 Dependence of the dielectric constant of electrolyte solution on ionic concentration. arXiv:1208.5169v1.Google Scholar
Gavryushov, S. & Linse, P. 2003 Polarization deficiency and excess free energy of ion hydration in electric fields. J. Phys. Chem. B 107, 7135–7142.Google Scholar
Glueckauf, E. 1964 Bulk dielectric constant of aqueous electrolyte solutions. Trans. Faraday Soc. 60, 1637–1645.CrossRefGoogle Scholar
Grosse, C. & Shilov, V. N. 1996 Theory of the low-frequency electrorotation of polystyrene particles in electrolyte solutions. J. Phys. Chem. 100, 1771–1778.Google Scholar
Hasted, J. B. 1973 Aqueous Dielectrics. Chapman and Hall.Google Scholar
Hasted, J. B., Ritson, D. M. & Collie, C. H. 1948 Dielectric properties of aqueous ionic solutions. Parts I and II. J. Chem. Phys. 16, 1–21.CrossRefGoogle Scholar
Hatlo, M. M., Van Roij, R. & Lue, L. 2012 The electric double layer at high surface potentials: The influence of excess ion polarizability. Europhys. Lett. 97, 28010.Google Scholar
Holovko, M. & Kapko, V. 2009 Ion association phenomena and static dielectric properties in electrolyte solution: application of the effective mean spherical approximation – mass action law approach. Acta Chim. Slov. 56, 203–208.Google Scholar
Hunter, R. J. 1981 Zeta Potential in Colloid Science. Academic.Google Scholar
Joshi, R. P., Qian, J., Schoenbach, K. H. & Schamiloglu, E. 2004 Microscopic analysis for water stressed by high electric fields in the prebreakdown regime. J. Appl. Phys. 96, 3617–3625.CrossRefGoogle Scholar
Jungwirth, P. & Tobias, D. 2001 Molecular structure of salt solutions: a new view of the interface with implications for heterogeneous atmospheric chemistry. J. Phys. Chem. B 105, 10468–10472.Google Scholar
Khair, A. S. & Squires, T. M. 2009 Ion steric effects on electrophoresis of a colloidal particle. J. Fluid Mech. 640, 343–356.Google Scholar
Kilic, M. S., Bazant, M. Z. & Ajdari, A. 2007a Steric effects in the dynamics of electrolytes at large applied voltages I. Double-layer charging. Phys. Rev. E 75, 021502.Google Scholar
Kilic, M. S., Bazant, M. Z. & Ajdari, A. 2007b Steric effects in the dynamics of electrolytes at large applied voltages II. Modified Poisson–Nernst–Planck equations. Phys. Rev. E 75, 021503.Google Scholar
Kunz, W. 2010 Specific ion effects in colloidal and biological systems. Curr. Opin. Colloid Interface Sci. 15, 34–39.Google Scholar
Kunz, W., Belloni, L., Bernard, O. & Nonham, B. W. 2004a Osmotic coefficients and surface tensions of aqueous electrolyte solutions: role of dispersion forces. J. Chem. Phys. B 108, 2398–2404.Google Scholar
Kunz, W., Henle, J. & Ninham, B. W. 2004b ‘Zur Lehre von der Wirkung der Salze’ (on the science of the effect of salts): Franz Hofmeister’s historical papers. Curr. Opin. Colloid Interface Sci. 9, 19–37.CrossRefGoogle Scholar
Kunz, W., Lo Nostro, P. & Ninham, B. W. 2004c The present state of affairs with Hofmeister effects. Curr. Opin. Colloid Interface Sci. 9, 1–18.CrossRefGoogle Scholar
Levy, A., Andelman, D. & Orland, H. 2012 Dielectric constant of ionic solutions: a field-theory approach. Phys. Rev. Lett. 108, 227801.Google Scholar
Lo Nostro, P. & Ninham, B. W. 2012 Hofmeister phenomena: an update on ion specificity in biology. Chem. Rev. 112, 2286–2322.Google Scholar
Lopez-Leon, T., Jodar-Reyes, A. B., Bastos-Gonzalez, D. & Ortega-Vinuesa, J. L. 2003 Hofmeister effects in the stability and electrophoretic mobility of polystyrene latex particles. J. Phys. Chem. B 107, 5696–5708.Google Scholar
Lopez-Leon, T., Jodar-Reyes, A. B., Ortega-Vinuesa, J. L. & Bastos-Gonzalez, D. 2005 Hofmeister effects on the colloidal stability of an IgG-coated polystyrene latex. J. Colloid Interface Sci. 284, 139–148.CrossRefGoogle ScholarPubMed
Lyklema, J. 1994 On the slip process in electrokinetics. Colloids Surf. A 92, 41–49.Google Scholar
Lyklema, J. 1995 Fundamentals of Interface and Colloid Science. Volume II: Solid-Liquid Interfaces. Academic.Google Scholar
Manciu, M. & Ruckenstein, E. 2003 Specific ion effects via ion hydration: I. Surface tension. Adv. Colloid Interface Sci. 105, 63–101.CrossRefGoogle ScholarPubMed
Netz, R. R. 2000 Debye-Huckel theory for slab geometries. Eur. Phys. J. E 3, 131–141.Google Scholar
Netz, R. R. 2001 Static van der Waals interactions in electrolytes. Eur. Phys. J. E 5, 189–205.Google Scholar
Netz, R. R. 2004 Water and ions at interfaces. Curr. Opin. Colloid Interface Sci. 9, 192–197.Google Scholar
O’Brien, R. W. 1983 The solution of the electrokinetic equations for colloidal particles with thin double layers. J. Colloid Interface Sci. 92, 204–216.CrossRefGoogle Scholar
O’Brien, R. W. & White, L. R. 1978 Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc. Faraday Trans. II 74, 1607–1626.Google Scholar
Ruckenstein, E. & Manciu, M. 2003 Specific ion effects via ion hydration: II. Double layer interaction. Adv. Colloid Interface Sci. 105, 177–200.CrossRefGoogle ScholarPubMed
Russel, W. B., Saville, D. A. & Schowalter, W. R. 1989 Colloidal Dispersions. Cambridge University Press.CrossRefGoogle Scholar
Salis, A., Cugia, F., Parsons, D. F., Ninham, B. W. & Monduzzi, M. 2012 Hofmeister series reversal for lysozyme by change in pH and salt concentrations: insights from electrophoretic mobility measurements. Phys. Chem. Chem. Phys. 14, 4343–4346.Google Scholar
Squires, T. M. & Quake, S. R. 2005 Microfluidics: fluid physics on the nanolter scale. Rev. Mod. Phys. 77, 977–1026.Google Scholar
Stone, H., Stroock, A. & Ajdari, A. 2004 Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 36, 381–411.Google Scholar
Storey, B. & Bazant, M. Z. 2012 Effects of electrostatic correlations on electrokinetic phenomena. Phys. Rev. E. 75, 021503.Google Scholar
Storey, B. D., Edwards, L. R., Kilic, M. S. & Bazant, M. Z. 2008 Steric effects on ac electro-osmosis in dilute electrolytes. Phys. Rev. E 77, 036317.Google Scholar
Viovy, J. L. 2000 Electrophoresis of DNA and other polyelectrolytes: physical mechanisms. Rev. Mod. Phys. 72, 813–872.Google Scholar
Vlachy, Y. 1999 Ionic effects beyond Poisson–Boltzmann theory. Annu. Rev. Phys. Chem. 50, 145–165.Google Scholar
Wei, Y. Z. & Sridhar, S. 1990 Dielectric spectroscopy up to 20 GHz of LiCl/ ${\mathrm{H} }_{2} \mathrm{O} $ solutions. J. Chem. Phys. 92, 923–928.Google Scholar
Wei, Y. Z. & Sridhar, S. 1992 Ion size effects on the dynamic and static dielectric properties of aqueous alkali solutions. J. Chem. Phys. 96, 4569–4573.Google Scholar
Zhao, H. 2010 On the influence of ion excluded volume (steric) effects on the double layer polarization of a non-conducting nano particle in an AC field. J. Phys. Chem. C 18, 8389–8397.CrossRefGoogle Scholar
Zhao, H. 2012 The influence of non-electrostatic ion–ion interactions on double layer capacitance. Phys. Rev. E 86, 051502.Google Scholar
Zwolak, M. & Di Ventra, M. 2005 Colloquium: physical approaches to DNA sequencing and detection. Rev. Mod. Phys. 80, 141–165.Google Scholar