Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T04:56:44.493Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial wave excitation and focusing in a liquid bounded by a frustum and a cylinder

Published online by Cambridge University Press:  18 June 2014

Marten Klein ,
Torsten Seelig ,
Michael V. Kurgansky ,
Abouzar Ghasemi V. ,
Ion Dan Borcia ,
Andreas Will ,
Eberhard Schaller ,
Christoph Egbers  and
Uwe Harlander
Marten Klein
Affiliation:
Department of Environmental Meteorology, Brandenburg University of Technology Cottbus-Senftenberg, Burger Chaussee 2, D-03044 Cottbus, Germany
Torsten Seelig
Affiliation:
Department of Aerodynamics and Fluid Mechanics, Brandenburg University of Technology Cottbus-Senftenberg, Siemens-Halske-Ring 14, D-03046 Cottbus, Germany
Michael V. Kurgansky
Affiliation:
A. M. Obukhov Institute of Atmospheric Physics, Russian Academy of Sciences, Pyzhevsky 3, 119017 Moscow, Russian Federation
Abouzar Ghasemi V.
Affiliation:
Department of Environmental Meteorology, Brandenburg University of Technology Cottbus-Senftenberg, Burger Chaussee 2, D-03044 Cottbus, Germany
Ion Dan Borcia
Affiliation:
Department of Aerodynamics and Fluid Mechanics, Brandenburg University of Technology Cottbus-Senftenberg, Siemens-Halske-Ring 14, D-03046 Cottbus, Germany
Andreas Will
Affiliation:
Department of Environmental Meteorology, Brandenburg University of Technology Cottbus-Senftenberg, Burger Chaussee 2, D-03044 Cottbus, Germany
Eberhard Schaller
Affiliation:
Department of Environmental Meteorology, Brandenburg University of Technology Cottbus-Senftenberg, Burger Chaussee 2, D-03044 Cottbus, Germany
Christoph Egbers
Affiliation:
Department of Aerodynamics and Fluid Mechanics, Brandenburg University of Technology Cottbus-Senftenberg, Siemens-Halske-Ring 14, D-03046 Cottbus, Germany
Uwe Harlander*
Affiliation:
Department of Aerodynamics and Fluid Mechanics, Brandenburg University of Technology Cottbus-Senftenberg, Siemens-Halske-Ring 14, D-03046 Cottbus, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The mechanism of localized inertial wave excitation and its efficiency is investigated for an annular cavity rotating with 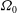$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\Omega _0$. Meridional symmetry is broken by replacing the inner cylinder with a truncated cone (frustum). Waves are excited by individual longitudinal libration of the walls. The geometry is non-separable and exhibits wave focusing and wave attractors. We investigated laboratory and numerical results for the Ekman number 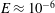$E\approx 10^{-6}$, inclination 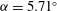$\alpha =5.71^\circ $ and libration amplitudes 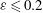$\varepsilon \leq 0.2$ within the inertial wave band 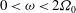$0 < \omega < 2\Omega _0$. Under the assumption that the inertial waves do not essentially affect the boundary-layer structure, we use classical boundary-layer analysis to study oscillating Ekman layers over a librating wall that is at an angle 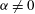$\alpha \neq 0$ to the axis of rotation. The Ekman layer erupts at frequency 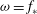$\omega =f_{*}$, where 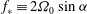$f_{*}\equiv 2 \Omega _0 \sin \alpha $ is the effective Coriolis parameter in a plane tangential to the wall. For the selected inclination this eruption occurs for the forcing frequency 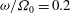$\omega /\Omega _0=0.2$. For the librating lids eruption occurs at 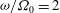$\omega /\Omega _0=2$. The study reveals that the frequency dependence of the total kinetic energy 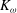$K_{\omega }$ of the excited wave field is strongly connected to the square of the Ekman pumping velocity 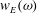$w_{{E}}(\omega )$ that, in the linear limit, becomes singular when the boundary layer erupts. This explains the frequency dependence of non-resonantly excited waves. By the localization of the forcing, the two configurations investigated, (i) frustum libration and (ii) lids together with outer cylinder in libration, can be clearly distinguished by their response spectra. Good agreement was found for the spatial structure of low-order wave attractors and periodic orbits (both characterized by a small number of reflections) in the frequency windows predicted by geometric ray tracing. For ‘resonant’ frequencies a significantly increased total bulk energy was found, while the energy in the boundary layer remained nearly constant. Inertial wave energy enters the bulk flow via corner beams, which are parallel to the characteristics of the underlying Poincaré problem. Numerical simulations revealed a mismatch between the wall-parallel mass fluxes near the corners. This leads to boundary-layer eruption and the generation of inertial waves in the corners.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 255 - 297
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agrawal, B. N. 1993 Dynamic characteristics of liquid motion in partially filled tanks of a spinning spacecraft. J. Guid. Control Dyn. 16, 636–640.CrossRefGoogle Scholar
Akselvoll, K. & Moin, P. 1996 An efficient method for temporal integration of the Navier–Stokes equations in confined axisymmetric geometries. J. Comput. Phys. 125 (2), 454–463.CrossRefGoogle Scholar
Aldridge, K. D. & Toomre, A. 1969 Axisymmetric inertial oscillations of a fluid in a rotating spherical container. J. Fluid Mech. 37 (2), 307–323.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Beardsley, R. C. 1970 An experimental study of inertial waves in a closed cone. Stud. Appl. Maths 49, 187–196.CrossRefGoogle Scholar
Boisson, J., Lamriben, C., Maas, L. R. M., Cortet, P.-P. & Moisy, F. 2012 Inertial waves and modes excited by the libration of a rotating cube. Phys. Fluids 24, 076602.CrossRefGoogle Scholar
Borcia, I. D. & Harlander, U. 2012 Inertial waves in a rotating annulus with inclined inner cylinder: comparing the spectrum of wave attractor frequency bands and the eigenspectrum in the limit of zero inclination. Theor. Comput. Fluid Dyn. 27, 397–413.CrossRefGoogle Scholar
Bordes, G., Venaille, A., Joubaud, S., Odier, P. & Dauxois, T. 2012 Experimental observation of a strong mean flow induced by internal gravity waves. Phys. Fluids 24 (8), 086602.CrossRefGoogle Scholar
Busse, F. H. 2010 Mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 650, 505–512.CrossRefGoogle Scholar
Busse, F. H. 2011 Zonal flow induced by longitudinal librations of a rotating cylindrical cavity. Physica D 240 (2), 208–211.CrossRefGoogle Scholar
Busse, F. H., Dormy, E., Simitev, R. & Soward, A. M. 2007 Mathematical Aspects of Natural Dynamos. Grenoble Sciences and CRC Press.Google Scholar
Calkins, M. A., Noir, J., Eldredge, J. D. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22 (8), 086602.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1991 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Choi, H.1993 Turbulent drag reduction: studies of feedback control and flow over riblets. PhD thesis, Stanford University.Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulations of turbulent-flow over riblets. J. Fluid Mech. 255, 503–539.CrossRefGoogle Scholar
Cortet, P.-P., Lamriben, C. & Moisy, F. 2010 Viscous spreading of an inertial wave beam in a rotating fluid. Phys. Fluids 22, 086603.CrossRefGoogle Scholar
Czarny, O., Serre, E., Bontoux, P. & Lueptow, R. M. 2003 Interaction between Ekman pumping and the centrifugal instability in Taylor–Couette flow. Phys. Fluids 15 (2), 467–477.CrossRefGoogle Scholar
Dominguez-Lerma, M. A., Ahlers, G. & Canell, D. S. 1985 Effects of ‘Kalliroscope’ flow visualization particles on rotating Couette–Taylor flow. Phys. Fluids 28, 1204–1206.CrossRefGoogle Scholar
Emery, W. J. & Thomson, R. E. 2001 Data Analysis Methods in Physical Oceanography. Elsevier.Google Scholar
Gostiaux, L. & Dauxois, T. 2007 Laboratory experiments on the generation of internal tidal beams over steep slopes. Phys. Fluids 19 (2), 028102.CrossRefGoogle Scholar
Greenspan, H. P. 1969 The Theory of Rotating Fluids, Cambridge Monographs on Mechanics and Applied Mathematics. Cambridge University Press, Reprint with corrections.Google Scholar
Greenspan, H. P. & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.CrossRefGoogle Scholar
Grigull, U., Straub, J. & Schiebener, P. 1990 Steam Tables in SI-Units/Wasserdampftafeln. Springer.CrossRefGoogle Scholar
Harlander, U. & Maas, L. R. M. 2006 Characteristics and energy rays of equatorially trapped, zonally symmetric internal waves. Meteorol. Z. 15, 439–450.CrossRefGoogle Scholar
Harlander, U. & Maas, L. R. M. 2007a Internal boundary layers in a well mixed equatorial atmosphere/ocean. Dyn. Atmos. Oceans 44, 1–28.CrossRefGoogle Scholar
Harlander, U. & Maas, L. R. M. 2007b Two alternatives for solving hyperbolic boundary value problems of geophysical fluid dynamics. J. Fluid Mech. 588, 331–351.CrossRefGoogle Scholar
Henderson, G. A. & Aldridge, K. D. 1992 A finite-element method for inertial waves in a frustum. J. Fluid Mech. 234, 317–327.CrossRefGoogle Scholar
Jouve, L. & Ogilvie, G. I. 2014 Direct numerical simulations of an inertial wave attractor in linear and nonlinear regimes. J. Fluid Mech. 745, 223–250.CrossRefGoogle Scholar
Kaltenbach, H.-J., Fatica, M., Mittal, R., Lund, T. S. & Moin, P. 1999 Study of flow in a planar asymmetric diffuser using large-eddy simulation. J. Fluid Mech. 390, 151–185.CrossRefGoogle Scholar
Kerswell, R. R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325.CrossRefGoogle Scholar
Koch, S., Harlander, U., Egbers, C. & Hollerbach, R. 2013 Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results. Fluid Dyn. Res. 45 (3), 035504.CrossRefGoogle Scholar
Le, H. & Moin, P. 1991 An improvement of fractional step methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 92 (2), 369–379.CrossRefGoogle Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Lopez, J. M. & Marques, F. 2011 Instabilities and inertial waves generated in a librating cylinder. J. Fluid Mech. 687, 171–193.CrossRefGoogle Scholar
Lopez, J. M. & Marques, F. 2014 Rapidly rotating cylinder flow with an oscillating sidewall. Phys. Rev. E 89, 013013.CrossRefGoogle ScholarPubMed
Maas, L. R. M. 2001 Wave focusing and ensuing mean flow due to symmetry breaking in rotating fluids. J. Fluid Mech. 437, 13–28.CrossRefGoogle Scholar
Maas, L. R. M. 2005 Wave attractors: linear yet nonlinear. Intl J. Bifurcation Chaos 15 (9), 2757–2782.CrossRefGoogle Scholar
Maas, L. R. M. & Harlander, U. 2007 Equatorial wave attractors and inertial oscillations. J. Fluid Mech. 570, 47–67.CrossRefGoogle Scholar
Maas, L. R. M. & Lam, F.-P. A. 1995 Geometric focusing of internal waves. J. Fluid Mech. 300, 1–41.CrossRefGoogle Scholar
Maas, L. R. M. & van Haren, J. J. M. 1987 Observations on the vertical structure of tidal and inertial currents in the central North Sea. J. Mar. Res. 45, 293–318.CrossRefGoogle Scholar
Manders, A. M. M. & Maas, L. R. M. 2003 Observations of inertial waves in a rectangular basin with one sloping boundary. J. Fluid Mech. 493, 59–88.CrossRefGoogle Scholar
Matisse, P. & Gorman, M. 1984 Neutrally buoyant anisotropic particles for flow visualization. Phys. Fluids 27, 759–760.CrossRefGoogle Scholar
McEwan, A. D. 1970 Inertial oscillations in a rotating fluid cylinder. J. Fluid Mech. 40 (3), 603–640.CrossRefGoogle Scholar
Messio, L., Morize, C., Rabaud, M. & Moisy, F. 2008 Experimental observation using particle image velocimetry of inertial waves in a rotating fluid. Exp. Fluids 44, 519–528.CrossRefGoogle Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 3030, 539–578.CrossRefGoogle Scholar
Morinishi, Y., Lund, T. S., Vasilyev, V. O. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143 (1), 90–124.CrossRefGoogle Scholar
Munk, W. H. 1980 Internal wave spectra at the buoyant and inertial frequencies. J. Phys. Oceanogr. 10, 1718–1728.2.0.CO;2>CrossRefGoogle Scholar
Noir, J., Calkins, M. A., Lasbleis, M., Cantwell, J. & Aurnou, J. M. 2010 Experimental study of libration-driven zonal flows in a straight cylinder. Phys. Earth Planet. Inter. 182, 98–106.CrossRefGoogle Scholar
Noir, J., Hemmerlin, F., Wicht, J., Baca, S. M. & Aurnou, J. M. 2009 An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans. Phys. Earth Planet. Inter. 173, 141–152.CrossRefGoogle Scholar
Orlandi, P. 2000 Fluid Flow Phenomena – A Numerical Toolkit. Kluwer.CrossRefGoogle Scholar
Ott, E. 1993 Chaos in Dynamical Systems. Cambridge University Press.Google Scholar
Perot, J. B. 1993 An analysis of the fractional step method. J. Comput. Phys. 108, 51–58.CrossRefGoogle Scholar
Phillips, O. M. 1963 Energy transfer in rotating fluids by reflection of inertial waves. Phys. Fluids 6 (4), 513–520.CrossRefGoogle Scholar
Prandle, D. 1982 The vertical structure of tidal currents and other oscillatory flows. Cont. Shelf Res. 1 (2), 191–207.CrossRefGoogle Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.CrossRefGoogle Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.CrossRefGoogle Scholar
Rosenfeld, M., Kwak, D. & Vinokur, M. 1991 A fractional step solution method for the unsteady incompressible Navier–Stokes equations in generalized coordinate systems. J. Comput. Phys. 94 (1), 102–137.CrossRefGoogle Scholar
Sauret, A., Cébron, D. & Le Bars, M. 2013 Sponateous generation of inertial waves from boundary turbulence in a librating sphere. J. Fluid Mech. 728, R5.CrossRefGoogle Scholar
Sauret, A., Cébron, D., Le Bars, M. & Le Dizès, S. 2012 Fluid flows in a librating cylinder. Phys. Fluids 24, 026603.CrossRefGoogle Scholar
Sauret, A. & Le Dizès, S. 2013 Libration-induced mean flow in a spherical shell. J. Fluid Mech. 718, 181–209.CrossRefGoogle Scholar
Schade, H. 1997 Tensoranalysis. Walter de Gruyter.Google Scholar
Smirnov, S. A., Baines, P. G., Boyer, D. L., Voropayev, S. I. & Srdic-Mitrovic, A. N. 2005 Long-time evolution of linearly stratified spin-up flows in axisymmetric geometries. Phys. Fluids 17, 016601.CrossRefGoogle Scholar
Swart, A., Manders, A., Harlander, U. & Maas, L. R. M. 2010 Experimental observation of strong mixing due to internal wave focusing over sloping terrain. Dyn. Atmos. Oceans 50, 16–34.CrossRefGoogle Scholar
Thompson, J. E., Warsi, Z. U. A. & Mastin, C. W. 1985 Numerical Grid Generation: Foundations and Applications. North-Holland.Google Scholar
Thorade, H. 1928 Gezeitenuntersuchungen in der Deutschen Bucht der Nordsee. Deutsche Seewarte 46 (3), 1–85. Friedrichsen, de Gruyter & Co.Google Scholar
Tilgner, A. 2007 Zonal wind driven by inertial modes. Phys. Rev. Lett. 99 (19), 194501.CrossRefGoogle ScholarPubMed
Tilgner, A. 2009 Rotational dynamics of the core. In Treatise in Geophysics, vol. 8. Elsevier.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.CrossRefGoogle Scholar
Wang, C.-Y. 1970 Cylindrical tank of fluid oscillating about a state of steady rotation. J. Fluid Mech. 41, 581–592.CrossRefGoogle Scholar
Zhang, K., Chan, K. H., Liao, X. & Aurnou, J. M. 2013 The non-resonant response of fluid in a rapidly rotating sphere undergoing longitudinal libration. J. Fluid Mech. 720, 212–235.CrossRefGoogle Scholar