Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T16:43:09.020Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial versus baroclinic instability of the Bickley jet in continuously stratified rotating fluid

Published online by Cambridge University Press:  04 March 2014

Bruno Ribstein ,
Riwal Plougonven Open the ORCID record for Riwal Plougonven [Opens in a new window]  and
Vladimir Zeitlin
Bruno Ribstein*
Affiliation:
LMD, Université Pierre et Marie Curie, and ENS, 24 rue Lhomond, 75005 Paris, France
Riwal Plougonven
Affiliation:
LMD, Université Pierre et Marie Curie, and ENS, 24 rue Lhomond, 75005 Paris, France LMD, Ecole Polytechnique, 91128 Palaiseau CEDEX, France
Vladimir Zeitlin
Affiliation:
LMD, Université Pierre et Marie Curie, and ENS, 24 rue Lhomond, 75005 Paris, France Institut Universitaire de France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper contains a detailed study of the inertial instability of a barotropic Bickley jet on the 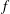$f$-plane in the continuously stratified primitive equations model, and a comparison of this essentially ageostrophic instability with the classical baroclinic one. Analytical and numerical investigation of the linear stability of the jet in the long-wave sector is performed for a range of Rossby and Burger numbers. The major results are that: (1) the standard symmetric inertial instability, appearing at high enough Rossby numbers, turns out to be the infinite-wavelength limit of an asymmetric inertial instability, this latter having the highest growth rate for a large range of vertical wavenumbers; (2) inertial instability coexists with the standard baroclinic instability, which becomes dominant at small Rossby numbers. Nonlinear saturation of the inertial instability of the jet with a superimposed random small-amplitude perturbation is then studied, using the Weather Research and Forecast model. It is shown that at first stages the inertial instability dominates. It is localized near the maximum of the anticyclonic shear and is associated with the highest attainable value of the vertical wavenumber. The saturation of the inertial instability leads to the homogenization of the geostrophic momentum in the unstable region. At later stages, another baroclinic instability develops, characterized by lower values of the vertical wavenumber. This instability saturates by forming large-scale vortices downstream. It is identified as the leading instability of a marginally inertially stable jet resulting from the initial one through homogenization of the geostrophic momentum. The rough scenario of the evolution of essentially ageostrophic jets is, thus, as follows: the inertial instability rapidly saturates and baroclinic instability takes over. It is shown that reorganization of the flow due to developing instabilities is an efficient source of inertia-gravity waves.

JFM classification

Instability: Instability Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 743 , 25 March 2014 , pp. 1 - 31
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bayly, B. J. 1987 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31, 56–64.CrossRefGoogle Scholar
Billant, P. & Gallaire, F. 2005 Generalized rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.Google Scholar
Bouchut, F., Ribstein, B. & Zeitlin, V. 2011 Inertial, barotropic, and baroclinic instabilities of the Bickley jet in two-layer rotating shallow water model. Phys. Fluids 23, 126601.CrossRefGoogle Scholar
Cairns, R. A. 1979 The role of negative energy waves in some instabilities of parallel flows. J. Fluid Mech. 92, 1–14.Google Scholar
Carnevale, G. F., Kloosterziel, R. C. & Orlandi, P. 2013 Inertial and barotropic instabilities of a free current in three-dimensional rotating flow. J. Fluid Mech. 725, 117–151.Google Scholar
Carnevale, G. F., Kloosterziel, R. C., Orlandi, P. & Van Sommeren, D. D. J. A. 2011 Predicting the aftermath of vortex breakup in rotating flow. J. Fluid Mech. 669, 90–119.Google Scholar
Clark, P. D. & Haynes, P. H. 1996 Inertial instability on an asymmetric low-latitude flow. Q. J. R. Meteorol. Soc. 122, 151–182.Google Scholar
Fritts, D. C. & Alexander, M. J. 2003 Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 41 (1), 1003.Google Scholar
Griffiths, S. D. 2003a The nonlinear evolution of zonally symmetric equatorial inertial instability. J. Fluid Mech. 474, 245–273.Google Scholar
Griffiths, S. D. 2003b Nonlinear vertical scale selection in equatorial inertial instability. J. Atmos. Sci. 60, 977–990.Google Scholar
Griffiths, S. D. 2008 The limiting form of inertial instability in geophysical flows. J. Fluid Mech. 605, 115–143.Google Scholar
Iga, K. 1999 Critical layer instability as a resonance between a non-singular mode and continous modes. Fluid Dyn. Res. 25, 63–86.Google Scholar
Kloosterziel, R. C. & Carnevale, G. F. 2008 Vertical scale selection in inertial instability. J. Fluid Mech. 594, 249–269.Google Scholar
Kloosterziel, R. C., Carnevale, G. F. & Orlandi, P. 2007a Inertial instability in rotating and stratified fluids: barotropic vortices. J. Fluid Mech. 583, 379–412.CrossRefGoogle Scholar
Kloosterziel, R. C., Orlandi, P. & Carnevale, G. F. 2007b Saturation of inertial instability in rotating planar shear flows. J. Fluid Mech. 583, 413–422.Google Scholar
Knox, J. A. & Harvey, V. L. 2005 Global climatology of inertial instability and Rossby wave breaking in the stratosphere. J. Geophys. Res. 110, D06108.Google Scholar
Lambaerts, J. G., Lapeyre, G. & Zeitlin, V. 2011 Moist vs dry barotropic instability in a shallow water model of the atmosphere with moist convection. J. Atmos. Sci. 68, 1234–1252.Google Scholar
Perret, G., Dubos, G. & Stegner, A. 2011 How large-scale and cyclogeostrophic barotropic instabilities favor the formation of anticyclonic vortices in the ocean. J. Phys. Oceanogr. 41, 303–328.Google Scholar
Plougonven, R. & Snyder, C. 2007 Inertia-gravity waves spontaneously generated by jets and fronts. Part I: Different baroclinic life cycles. J. Atmos. Sci. 64, 2502–2520.Google Scholar
Plougonven, R. & Zeitlin, V. 2005 Lagrangian approach to the geostrophic adjustment of frontal anomalies in a stratified fluid. Geophys. Astrophys. Fluid Dyn. 99, 101–135.Google Scholar
Plougonven, R. & Zeitlin, V. 2009 Nonlinear development of inertial instability in a barotropic shear. Phys. Fluids 21, 106601.Google Scholar
Poulin, F. L. & Flierl, G. R. 2003 The nonlinear evolution of barotropically unstable jets. J. Phys. Oceanogr. 33, 2173–2192.2.0.CO;2>CrossRefGoogle Scholar
Sato, K. & Dunkerton, T. J. 2002 Layered structure associated with low potential vorticity near the tropopause seen in high-resolution radiosondes over Japan. J. Atmos. Sci. 59, 2782–2800.Google Scholar
Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Barker, D. M., Duda, M. G., Huang, X.-Y., Wang, W. & Powers, J. G.2012 A description of the Advanced Research Weather Research and Forecast model Version 3. In NCAR Technical Note.Google Scholar
Stevens, D. E. & Ciesielski, P. E. 1986 Inertial instability of horizontally sheared flow away from the Equator. J. Atmos. Sci. 43, 2845–2856.2.0.CO;2>CrossRefGoogle Scholar
Trefethen, L. N. 2000 Spectral Methods in Matlab. SIAM.Google Scholar
Wicker, L. J. & Skamarock, W. C. 2002 Time splitting methods for elastic models using forward time schemes. Mon. Wea. Rev. 130, 2088–2097.Google Scholar