Article contents
The impact of dynamic roughness elements on marginally separated boundary layers
Published online by Cambridge University Press: 19 September 2018
Abstract
It has been shown experimentally that dynamic roughness elements – small bumps embedded within a boundary layer, oscillating at a fixed frequency – are able to increase the angle of attack at which a laminar boundary layer will separate from the leading edge of an airfoil (Grager et al., in 6th AIAA Flow Control Conference, 2012, pp. 25–28). In this paper, we attempt to verify that such an increase is possible by considering a two-dimensional dynamic roughness element in the context of marginal separation theory, and suggest the mechanisms through which any increase may come about. We will show that a dynamic roughness element can increase the value of 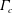 $\unicode[STIX]{x1D6E4}_{c}$ as compared to the clean airfoil case;
$\unicode[STIX]{x1D6E4}_{c}$ as compared to the clean airfoil case; 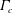 $\unicode[STIX]{x1D6E4}_{c}$ represents, mathematically, the critical value of the parameter
$\unicode[STIX]{x1D6E4}_{c}$ represents, mathematically, the critical value of the parameter 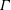 $\unicode[STIX]{x1D6E4}$ below which a solution exists in the governing equations and, physically, the maximum angle of attack possible below which a laminar boundary layer will remain predominantly attached to the surface. Furthermore, we find that the dynamic roughness element impacts on the perturbation pressure gradient in two possible ways: either by decreasing the magnitude of the adverse pressure peak or by increasing the streamwise extent in which favourable pressure perturbations exist. Finally, we discover that the marginal separation bubble does not necessarily have to exist at
$\unicode[STIX]{x1D6E4}$ below which a solution exists in the governing equations and, physically, the maximum angle of attack possible below which a laminar boundary layer will remain predominantly attached to the surface. Furthermore, we find that the dynamic roughness element impacts on the perturbation pressure gradient in two possible ways: either by decreasing the magnitude of the adverse pressure peak or by increasing the streamwise extent in which favourable pressure perturbations exist. Finally, we discover that the marginal separation bubble does not necessarily have to exist at 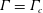 $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{c}$ in the time-averaged flow and that full breakaway separation can therefore occur as a result of the bursting of transient bubbles existing within the length scale of marginal separation theory.
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{c}$ in the time-averaged flow and that full breakaway separation can therefore occur as a result of the bursting of transient bubbles existing within the length scale of marginal separation theory.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 3
- Cited by



