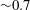1. Introduction
Vessel wake waves add energy to coastal systems wherever they occur. Their contribution is obviously negligible on high-energy coasts that are open to large ocean waves. In semi-sheltered and coastal areas exposed to significant ship traffic, waves from ship wakes can be a major factor in the dynamics of the coastal zone (Parnell & Kofoed-Hansen Reference Parnell and Kofoed-Hansen2001; Soomere Reference Soomere2007). In sensitive areas (e.g. near harbours or nature reserves) speed restrictions are often imposed in an effort to control the impact of wake waves. However, this type of blanket regulation represents a crude approach, as it ignores the diversity of wake characteristics for individual ships (Stumbo et al. Reference Stumbo, Fox, Dvorak and Elliot1999; Varyani Reference Varyani2006). In order to improve management of ship wake impact at the coast it is necessary to identify characteristic wake structures and link these to individual ships. Many of the common practices in wind wave analysis, however, are difficult to apply to ship wake waves as their basic parameters vary not only over the course of a single wake event but also show extremely high spatial variability (Torsvik & Soomere Reference Torsvik and Soomere2008).
The physics of ship wake formation is a complex field of research that includes a rich variety of water wave phenomena, from linear wave groups, the geometry of which is discussed in standard textbooks on fluid dynamics (e.g. Lamb Reference Lamb1932; Lighthill Reference Lighthill1978; Kundu Reference Kundu1990), to intricate nonlinear mechanisms of generation, propagation and interactions of various wake components, including interactions with ambient waves (Zhu, Liu & Yue Reference Zhu, Liu and Yue2008). Linear wake components that are stationary in a suitably chosen coordinate system have been described by Lord Kelvin (e.g. Newman Reference Newman1977). The mathematical issues relevant for this type of wake system are detailed in textbooks (e.g. Kuznetsov, Maz’ya & Vainberg Reference Kuznetsov, Maz’ya and Vainberg2002). It is common to use the term ‘Kelvin wake’ for wave systems that are steady in the ship-fixed coordinate system, when the ship is moving with constant speed in deep water, and along a straight line (figure 1). The Kelvin wake consists of transverse waves that propagate in the direction of the ship, and divergent waves that propagate at an oblique angle with respect to the direction of ship movement. The ship wake is confined to a wedge-shaped region, which in deep water has a half-angle (Kelvin angle) of
![]() ${\it\alpha}=\arcsin (1/3)\approx 19.5^{\circ }$
, and at the outer edge of this wedge the interaction between the divergent and transverse wave components leads to the formation of so-called cusp waves (Zilman, Zapolski & Marom Reference Zilman, Zapolski and Marom2004). Linear wave theory is also applicable for shallow-water wave patterns (Yih & Zhu Reference Yih and Zhu1989a
,Reference Yih and Zhu
b
), in which case
${\it\alpha}=\arcsin (1/3)\approx 19.5^{\circ }$
, and at the outer edge of this wedge the interaction between the divergent and transverse wave components leads to the formation of so-called cusp waves (Zilman, Zapolski & Marom Reference Zilman, Zapolski and Marom2004). Linear wave theory is also applicable for shallow-water wave patterns (Yih & Zhu Reference Yih and Zhu1989a
,Reference Yih and Zhu
b
), in which case
![]() ${\it\alpha}$
may increase, theoretically reaching a maximum of 90°. There is some confusion in the literature about the terminology for steady ship wakes. In this paper we use the terms ‘Kelvin wake’ and ‘Kelvin angle’ exclusively for the steady deep-water wave pattern and its corresponding wedge half-angle as described by linear wave theory.
${\it\alpha}$
may increase, theoretically reaching a maximum of 90°. There is some confusion in the literature about the terminology for steady ship wakes. In this paper we use the terms ‘Kelvin wake’ and ‘Kelvin angle’ exclusively for the steady deep-water wave pattern and its corresponding wedge half-angle as described by linear wave theory.

Figure 1. The structure of the Kelvin ship wake. Solid lines indicate wave crests for the divergent and transversal wave systems. The dashed line indicate the outer edges of the wake region. Note the phase shift between the divergent and transversal wave systems at the cusp line (see e.g. Newman Reference Newman1977).
The Kelvin wake theory imposes a restriction on the phase speed admissible for waves propagating at any specific angle relative to the direction of ship movement, but does not impose any restriction on how the wave amplitude is distributed over the different wave components. The wave amplitude depends on the hull shape and associated water displacement, but also the speed–length ratio, which can be defined in terms of the length-based Froude number
![]() $F_{L}=U/\sqrt{gL_{s}}$
, where
$F_{L}=U/\sqrt{gL_{s}}$
, where
![]() $U$
is the ship speed,
$U$
is the ship speed,
![]() $g$
is the gravitational acceleration and
$g$
is the gravitational acceleration and
![]() $L_{s}$
is the length of the ship. The transverse wave resistance usually has a maximum at
$L_{s}$
is the length of the ship. The transverse wave resistance usually has a maximum at
![]() $F_{L}=1/\sqrt{{\rm\pi}}\approx 0.5$
, for which the bow and stern transverse wave systems amplify each other (Faltinsen Reference Faltinsen2005). The divergent wave contribution is dominant when
$F_{L}=1/\sqrt{{\rm\pi}}\approx 0.5$
, for which the bow and stern transverse wave systems amplify each other (Faltinsen Reference Faltinsen2005). The divergent wave contribution is dominant when
![]() $F_{L}\gtrsim 0.6$
, whereas for smaller values of
$F_{L}\gtrsim 0.6$
, whereas for smaller values of
![]() $F_{L}$
the wave resistance characteristics vary depending on the hull shape. In shallow water the wave making resistance will also depend on the local water depth
$F_{L}$
the wave resistance characteristics vary depending on the hull shape. In shallow water the wave making resistance will also depend on the local water depth
![]() $d$
, as expressed by the depth-based Froude number
$d$
, as expressed by the depth-based Froude number
![]() $F_{d}=U/\sqrt{gd}$
.
$F_{d}=U/\sqrt{gd}$
.
The classical Kelvin structure (figure 1) is representative for ship wakes generated at low Froude numbers (
![]() $F_{L},F_{d}<0.5$
). However, progress in shipbuilding, especially the increase in the power of propulsion systems, has led to the introduction of ships that are able to sail at large Froude numbers. Such ships often produce a fascinating variety of nonlinear components of disturbances, ranging from Korteweg–de Vries (KdV)-type precursor solitons, quasi-stable and undular bores (Lee, Yates & Wu Reference Lee, Yates and Wu1989; Stumbo et al.
Reference Stumbo, Fox, Dvorak and Elliot1999; Gourlay Reference Gourlay2001) to envelope solitons described in the framework of either the nonlinear Schrödinger equation (Brown et al.
Reference Brown, Buchsbaum, Hall, Penhune, Schnitt, Watson and Wyatt1989; Mei & Naciri Reference Mei and Naciri1991) or the Zakharov equation (Zhu et al.
Reference Zhu, Liu and Yue2008). It is not unusual for wave wakes generated by high-speed ships to include almost a dozen components with greatly differing physical properties (Reed & Milgram Reference Reed and Milgram2002; Soomere Reference Soomere2007). These wake systems can maintain their characteristics over large distances (order of many kilometres) and times (order of hours) and significantly impact on relatively remote coasts (e.g. Parnell & Kofoed-Hansen Reference Parnell and Kofoed-Hansen2001; Soomere Reference Soomere2007).
$F_{L},F_{d}<0.5$
). However, progress in shipbuilding, especially the increase in the power of propulsion systems, has led to the introduction of ships that are able to sail at large Froude numbers. Such ships often produce a fascinating variety of nonlinear components of disturbances, ranging from Korteweg–de Vries (KdV)-type precursor solitons, quasi-stable and undular bores (Lee, Yates & Wu Reference Lee, Yates and Wu1989; Stumbo et al.
Reference Stumbo, Fox, Dvorak and Elliot1999; Gourlay Reference Gourlay2001) to envelope solitons described in the framework of either the nonlinear Schrödinger equation (Brown et al.
Reference Brown, Buchsbaum, Hall, Penhune, Schnitt, Watson and Wyatt1989; Mei & Naciri Reference Mei and Naciri1991) or the Zakharov equation (Zhu et al.
Reference Zhu, Liu and Yue2008). It is not unusual for wave wakes generated by high-speed ships to include almost a dozen components with greatly differing physical properties (Reed & Milgram Reference Reed and Milgram2002; Soomere Reference Soomere2007). These wake systems can maintain their characteristics over large distances (order of many kilometres) and times (order of hours) and significantly impact on relatively remote coasts (e.g. Parnell & Kofoed-Hansen Reference Parnell and Kofoed-Hansen2001; Soomere Reference Soomere2007).
The bulk of the existing ship-wave research has been concentrated on wave components that are stationary in the ship coordinate system. However, substantial unsteady wave components can be generated at depth Froude numbers
![]() $F_{d}>0.6$
(Lee et al.
Reference Lee, Yates and Wu1989), including ship-generated KdV solitons that usually travel faster than the ship (Mei Reference Mei1986; Lee et al.
Reference Lee, Yates and Wu1989; Grimshaw, Pelinovsky & Sakov Reference Grimshaw, Pelinovsky and Sakov1996), the development of a related, gradually lengthening depression (Akylas Reference Akylas1984; Katsis & Akylas Reference Katsis and Akylas1987) causing the squat phenomenon (Naghdi & Rubin Reference Naghdi and Rubin1984; Gourlay Reference Gourlay2006), and possibly associated undular bores (El, Grimshaw & Smyth Reference El, Grimshaw and Smyth2006). At
$F_{d}>0.6$
(Lee et al.
Reference Lee, Yates and Wu1989), including ship-generated KdV solitons that usually travel faster than the ship (Mei Reference Mei1986; Lee et al.
Reference Lee, Yates and Wu1989; Grimshaw, Pelinovsky & Sakov Reference Grimshaw, Pelinovsky and Sakov1996), the development of a related, gradually lengthening depression (Akylas Reference Akylas1984; Katsis & Akylas Reference Katsis and Akylas1987) causing the squat phenomenon (Naghdi & Rubin Reference Naghdi and Rubin1984; Gourlay Reference Gourlay2006), and possibly associated undular bores (El, Grimshaw & Smyth Reference El, Grimshaw and Smyth2006). At
![]() $F_{d}>1$
the ship velocity exceeds the maximum local wave group velocity as attained by linear wave theory. In this case the surface disturbances in the vicinity of the ship are essentially forced oscillations and the process of their conversion into free waves is not necessarily stationary with respect to the ship (Choi et al.
Reference Choi, Bai, Kim and Cho1990; Li & Sclavounos Reference Li and Sclavounos2002). An increase in the ship speed is, most probably, associated with an increase in the proportion of non-stationary components of the wave wake, and consequently, a widening of the frequency spectrum of the wake. A series of recent studies has also been devoted to the investigation of wake patterns for length Froude numbers
$F_{d}>1$
the ship velocity exceeds the maximum local wave group velocity as attained by linear wave theory. In this case the surface disturbances in the vicinity of the ship are essentially forced oscillations and the process of their conversion into free waves is not necessarily stationary with respect to the ship (Choi et al.
Reference Choi, Bai, Kim and Cho1990; Li & Sclavounos Reference Li and Sclavounos2002). An increase in the ship speed is, most probably, associated with an increase in the proportion of non-stationary components of the wave wake, and consequently, a widening of the frequency spectrum of the wake. A series of recent studies has also been devoted to the investigation of wake patterns for length Froude numbers
![]() $F_{L}\gtrsim 0.5$
, for which recent observations have highlighted that the dominant wake wedge angle is significantly less than the Kelvin angle, and that the angle decreases with increasing ship speed (Rabaud & Moisy Reference Rabaud and Moisy2013). However, these observations are not necessarily in contradiction with linear Kelvin wake theory (Darmon, Benzaquen & Raphael Reference Darmon, Benzaquen and Raphael2014; Noblesse et al.
Reference Noblesse, He, Zhu, Hong, Zhang, Zhu and Yang2014), but indicate that the highest waves may not coincide with the cusp line wave system for ships sailing in the high Froude number regime, making it difficult to determine the actual edge of the wake wedge. The wake pattern may also be influenced by shear flow (Ellingsen Reference Ellingsen2014), and by nonlinear wave effects due to large wave amplitudes (Pethiyagoda, McCue & Moroney Reference Pethiyagoda, McCue and Moroney2014). It is therefore to be expected that measurements of ship wake events can contain a large range of pattern variability depending on ship characteristics as well as local environment conditions.
$F_{L}\gtrsim 0.5$
, for which recent observations have highlighted that the dominant wake wedge angle is significantly less than the Kelvin angle, and that the angle decreases with increasing ship speed (Rabaud & Moisy Reference Rabaud and Moisy2013). However, these observations are not necessarily in contradiction with linear Kelvin wake theory (Darmon, Benzaquen & Raphael Reference Darmon, Benzaquen and Raphael2014; Noblesse et al.
Reference Noblesse, He, Zhu, Hong, Zhang, Zhu and Yang2014), but indicate that the highest waves may not coincide with the cusp line wave system for ships sailing in the high Froude number regime, making it difficult to determine the actual edge of the wake wedge. The wake pattern may also be influenced by shear flow (Ellingsen Reference Ellingsen2014), and by nonlinear wave effects due to large wave amplitudes (Pethiyagoda, McCue & Moroney Reference Pethiyagoda, McCue and Moroney2014). It is therefore to be expected that measurements of ship wake events can contain a large range of pattern variability depending on ship characteristics as well as local environment conditions.
While challenging for standard spectral analysis methods (e.g. Fourier series), the spatially localized, transient structure of ship wakes is naturally described by local transforms such as windowed Fourier transforms and wavelet transforms. The local-transform method was first used for ship wake analysis by Wyatt & Hall (Reference Wyatt and Hall1988), and has been used on a few subsequent occasions (e.g. Brown et al. Reference Brown, Buchsbaum, Hall, Penhune, Schnitt, Watson and Wyatt1989; Milgram, Peltzer & Griffin Reference Milgram, Peltzer and Griffin1993), mostly as an analysis tool for SAR images. The potential value of this method of analysing ship-wake impacts on the coast has only recently been highlighted by Sheremet, Gravois & Tian (Reference Sheremet, Gravois and Tian2013).
The data analysed in this study have been collected at coastal sections close to a shipping lane with heavy traffic, with different high-speed ferries passing at regular time intervals. This enables the identification of wakes from individual ships, and a comparison of wake characteristics associated with different vessels. The wake events we analyse are generated by large passenger ferries for which we can assume that
![]() $F_{L}\ll 0.5$
, but where
$F_{L}\ll 0.5$
, but where
![]() $F_{d}$
can reach values of
$F_{d}$
can reach values of
![]() ${\sim}0.7$
along certain sections of the route, hence some shallow-water effects can be expected. However, as
${\sim}0.7$
along certain sections of the route, hence some shallow-water effects can be expected. However, as
![]() $F_{d}$
varies considerably along the ship route due to local depth variation (Torsvik et al.
Reference Torsvik, Didenkulova, Soomere and Parnell2009), and we do not know the exact points of origin for the wake components that we record, we have performed the analysis based on deep-water linear wave theory which is invariant with respect to the water depth.
$F_{d}$
varies considerably along the ship route due to local depth variation (Torsvik et al.
Reference Torsvik, Didenkulova, Soomere and Parnell2009), and we do not know the exact points of origin for the wake components that we record, we have performed the analysis based on deep-water linear wave theory which is invariant with respect to the water depth.
This paper is a continuation of the work presented in Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013). While the focus of Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013) was primarily the descriptive, qualitative characterization of ship wake events, the main objective of this paper is quantification of key ship wake parameters based on wake structure analysis. The analysis is based on the same data set and basic procedures for conversion to the spectrogram representation as were presented in Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013). Hence only a short overview of the measurement program and an outline of the data analysis method have been included in § 2 of this paper. However, the theory of the wake signal analysis for a fixed observer (§ 2.2) was not included in Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013). Figures 5 and 6 are similar to figures published in Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013), but have been included here in order to make the paper self-contained. The key new elements are presented in §§ 3 and 4, starting with the identification of ship wake structures in the spectrograms (§ 3.1), specifically the identification of characteristic wake features that are persistent for individual ships, including transverse and divergent wake components. This is followed by a demonstration of how the wake structure analysis, when used in combination with the classical Kelvin wake theory, can be used to obtain estimates for the ship sailing speed (§ 2.2.2) and distance between the ship track and the measurement point (§ 3.3). The wake structure analysis also provides the basis for estimating the energy content of different wake components, which is discussed in § 4. Discussion of the results and main conclusions are given in § 5.
2. Field experiment and analysis methods
2.1. Wake measurements
Measurements of ship wakes were performed in the Tallinn Bay area in the summer months of 2008 and 2009. Tallinn Bay is an area in the north-eastern Baltic Sea, of approximately
![]() $10~\text{km}\times 20~\text{km}$
in size, which is open to the Gulf of Finland to the north and partly to the west, with the city of Tallinn located at the south end of the bay (figure 2). The coastline shape and location of the islands of Naissaar and Aegna offer protection from wind waves from most directions, with the roughest seas produced during north–northwestern (NNW) storms. Peak periods of wind waves are usually below 3 s. The annual maximum is usually in the range of 4–6 s, but can in exceptional cases exceed 8 s (Soomere Reference Soomere2005).
$10~\text{km}\times 20~\text{km}$
in size, which is open to the Gulf of Finland to the north and partly to the west, with the city of Tallinn located at the south end of the bay (figure 2). The coastline shape and location of the islands of Naissaar and Aegna offer protection from wind waves from most directions, with the roughest seas produced during north–northwestern (NNW) storms. Peak periods of wind waves are usually below 3 s. The annual maximum is usually in the range of 4–6 s, but can in exceptional cases exceed 8 s (Soomere Reference Soomere2005).

Figure 2. Map of (a) the Gulf of Finland and (b) the Tallinn Bay area. Experimental sites at Aegna and Pikakari are indicated on the map. The yellow lines indicate typical routes for ferries on the Tallinn–Helsinki link, with north-bound routes located east of south-bound routes.
Wave measurements were conducted at two sites, located on both sides of the ship routes (see Parnell et al.
Reference Parnell, Delpeche, Didenkulova, Dolphin, Erm, Kask, Kelpšaite, Kurennoy, Quak, Räämet, Soomere, Terentjeva, Torsvik and Zaitseva-Pärnaste2008; Didenkulova & Soomere Reference Didenkulova and Soomere2011; Kurennoy, Parnell & Soomere Reference Kurennoy, Parnell and Soomere2011 for detailed descriptions of the experiments). In 2008, wave observations were collected at a small mixed gravel–sand beach adjacent to a jetty, on the south-western (SW) coast of Aegna, a small (approximately
![]() $1.5~\text{km}\times 2~\text{km}$
) island 1.5 km north of the Viimsi Peninsula, at the northern entrance of Tallinn Bay (figure 2). In 2009, a similar experiment was conducted at Pikakari Beach on the Paljassaare Peninsula, on the SW coast of Tallinn Bay, a few kilometres to the north–west (NW) of Tallinn ferry terminal, and approximately 2.4 km from the ferry sailing line. In contrast to the Aegna site, the Pikakari site was most of the time sheltered from the large waves generated by westerly (or NNW) winds.
$1.5~\text{km}\times 2~\text{km}$
) island 1.5 km north of the Viimsi Peninsula, at the northern entrance of Tallinn Bay (figure 2). In 2009, a similar experiment was conducted at Pikakari Beach on the Paljassaare Peninsula, on the SW coast of Tallinn Bay, a few kilometres to the north–west (NW) of Tallinn ferry terminal, and approximately 2.4 km from the ferry sailing line. In contrast to the Aegna site, the Pikakari site was most of the time sheltered from the large waves generated by westerly (or NNW) winds.
The free surface elevation was measured using a LOG_aLevel echosounder mounted at approximately 2.5 m above the mean water level, on a tripod located near the 2.6 m isobath. At both measurement sites the tripod was situated approximately 100 m offshore from the shoreline. The instrument sampled the surface elevation continuously at 5 Hz over time periods of several days. The analysis in this paper is based on continuous 24 h time records: seven records from Aegna in 2008 and six records from Pikakari Beach in 2009.
2.2. Wake signal analysis for a fixed observer
The wake properties for high-speed vessels in shallow waters depend on several factors, such as the depth- and length-based Froude numbers and the specific bathymetry and coastline geometry. For the purpose of wake analysis it is nevertheless instructive to apply a reference case defined by the classical Kelvin structure (figure 1) with waves generated at low Froude numbers and propagating in deep water without any influence from the coast (Newman Reference Newman1977). In most cases, even in moderately shallow water and Froude numbers up to 0.5, the ship wakes will deviate only slightly from the classical case. The geometry of one half of the Kelvin wake wedge is shown in figure 3, for a ship (point
![]() $A$
) moving to the right at constant speed
$A$
) moving to the right at constant speed
![]() $U$
. According to the Kelvin wake theory the half-angle of the wedge is determined by
$U$
. According to the Kelvin wake theory the half-angle of the wedge is determined by
![]() $\sin {\it\alpha}=1/3$
, hence
$\sin {\it\alpha}=1/3$
, hence
![]() ${\it\alpha}\approx 19.5^{\circ }$
.
${\it\alpha}\approx 19.5^{\circ }$
.

Figure 3. The geometry of the Kelvin wake produced by a ship (point
![]() $A$
) moving to the right at a constant speed
$A$
) moving to the right at a constant speed
![]() $U$
. The line
$U$
. The line
![]() $\overline{AB}$
is the sailing line. The line
$\overline{AB}$
is the sailing line. The line
![]() $\overline{AP}$
marks the wedge edge of the wake.
$\overline{AP}$
marks the wedge edge of the wake.
Waves within the wedge have a stationary phase in the reference frame of the moving ship, and therefore propagate with the phase speed
where
![]() ${\it\omega}$
is the angular frequency,
${\it\omega}$
is the angular frequency,
![]() $k$
is the wavenumber, and
$k$
is the wavenumber, and
![]() ${\it\theta}$
is the angle of propagation relative to the sailing line. By using the deep-water approximation for the dispersion relation
${\it\theta}$
is the angle of propagation relative to the sailing line. By using the deep-water approximation for the dispersion relation
![]() ${\it\omega}^{2}=gk$
, we obtain the angular frequency of a wake wave:
${\it\omega}^{2}=gk$
, we obtain the angular frequency of a wake wave:
The cusp waves coinciding with the wedge edge propagate at an angle
![]() ${\it\theta}={\it\phi}_{P}$
, determined by
${\it\theta}={\it\phi}_{P}$
, determined by
![]() $\cos {\it\phi}_{P}=\sqrt{2/3}$
, hence
$\cos {\it\phi}_{P}=\sqrt{2/3}$
, hence
![]() ${\it\phi}_{P}\approx 35.3^{\circ }$
. Transverse waves propagate at angles less than this value, reaching
${\it\phi}_{P}\approx 35.3^{\circ }$
. Transverse waves propagate at angles less than this value, reaching
![]() ${\it\theta}=0^{\circ }$
for waves propagating along the sailing line, and divergent waves have angles
${\it\theta}=0^{\circ }$
for waves propagating along the sailing line, and divergent waves have angles
![]() ${\it\theta}>{\it\phi}_{P}$
.
${\it\theta}>{\it\phi}_{P}$
.
The spectrograms are usually plotted with frequency
![]() $f$
(Hz) along the
$f$
(Hz) along the
![]() $y$
-axis, and it is therefore convenient to use this variable instead of
$y$
-axis, and it is therefore convenient to use this variable instead of
![]() ${\it\omega}$
(
${\it\omega}$
(
![]() $2{\rm\pi}\,\,\text{Hz}$
) in the following analysis. The wave energy propagates with the group speed
$2{\rm\pi}\,\,\text{Hz}$
) in the following analysis. The wave energy propagates with the group speed
![]() $c_{g}$
, and
$c_{g}$
, and
![]() $c_{g}=c_{p}/2$
in deep water. Waves generated at point
$c_{g}=c_{p}/2$
in deep water. Waves generated at point
![]() $B$
are therefore confined within a semi-circle
$B$
are therefore confined within a semi-circle
![]() $BC$
with a tangent point
$BC$
with a tangent point
![]() $P$
along the cusp line of the wake wedge.
$P$
along the cusp line of the wake wedge.
An observer at rest standing at a distance
![]() $Y$
from the ship track will observe the approaching cusp wave system at point
$Y$
from the ship track will observe the approaching cusp wave system at point
![]() $P$
. The Kelvin wake is steady in the reference frame of the ship, therefore the entire wake structure moves with the speed
$P$
. The Kelvin wake is steady in the reference frame of the ship, therefore the entire wake structure moves with the speed
![]() $U$
relative to an observer at rest. In the reference frame of the ship, an observer at rest appears to move to the left with a constant speed
$U$
relative to an observer at rest. In the reference frame of the ship, an observer at rest appears to move to the left with a constant speed
![]() $U$
along the line
$U$
along the line
![]() $\overline{PQ}$
, and observes waves generated at point
$\overline{PQ}$
, and observes waves generated at point
![]() $B$
downstream of the ship at points
$B$
downstream of the ship at points
![]() $P$
at time
$P$
at time
![]() $t_{1}$
and
$t_{1}$
and
![]() $Q$
at time
$Q$
at time
![]() $t_{2}$
. A wave record at the stationary observation point will therefore correspond to the wave distribution along the segment
$t_{2}$
. A wave record at the stationary observation point will therefore correspond to the wave distribution along the segment
![]() $\overline{PQ}$
, hence the measured wave record will primarily depend on the ship velocity
$\overline{PQ}$
, hence the measured wave record will primarily depend on the ship velocity
![]() $U$
and the distance
$U$
and the distance
![]() $Y$
from the ship track.
$Y$
from the ship track.
2.2.1. The time–frequency analysis of ship wakes
Recently, time–frequency analysis techniques (see Sheremet et al. Reference Sheremet, Gravois and Tian2013 for a discussion of the method) were shown to provide useful information about ship-wake signals. The transient wakes were found to produce a distinct sliding-frequency signal (chirp) that allows the identification and study of the wake structure even in the presence of a broad-band wind-wave background.

Figure 4. Spectrogram representation of the classical Kelvin wake wave components generated by a moving point pressure acting on the surface, as recorded by a stationary observer. A time series of surface displacement
![]() ${\it\eta}$
is shown above the corresponding spectrogram representation of the wave record, and the colour scale is logarithmic in terms of the power spectral density. (a–c) Point pressure speed
${\it\eta}$
is shown above the corresponding spectrogram representation of the wave record, and the colour scale is logarithmic in terms of the power spectral density. (a–c) Point pressure speed
![]() $U=5~\text{m}~\text{s}^{-1}$
; (d–f) point pressure speed
$U=5~\text{m}~\text{s}^{-1}$
; (d–f) point pressure speed
![]() $U=10~\text{m}~\text{s}^{-1}$
. Left to right: increasing distance
$U=10~\text{m}~\text{s}^{-1}$
. Left to right: increasing distance
![]() $Y$
from moving point pressure source to observer: (a,d)
$Y$
from moving point pressure source to observer: (a,d)
![]() $Y=1~\text{km}$
; (b,e)
$Y=1~\text{km}$
; (b,e)
![]() $Y=2~\text{km}$
; (c, f)
$Y=2~\text{km}$
; (c, f)
![]() $Y=4~\text{km}$
.
$Y=4~\text{km}$
.
The capabilities of the time–frequency analysis are illustrated using the Kelvin deep-water wake generated by a moving point pressure acting on the surface (figure 4), which is here assumed to represent a moving ship. Following Newman (Reference Newman1977), for a ship moving along the
![]() $x$
-axis in the positive direction with the
$x$
-axis in the positive direction with the
![]() $y$
-axis perpendicular to the sailing line, the far-field asymptotic approximation of the wake in the reference frame of the ship can be written in polar coordinates
$y$
-axis perpendicular to the sailing line, the far-field asymptotic approximation of the wake in the reference frame of the ship can be written in polar coordinates
![]() $(r,{\it\theta})$
as
$(r,{\it\theta})$
as
where we assume that
![]() $x<0$
within the wake region, and the
$x<0$
within the wake region, and the
![]() $(x,y)$
coordinates are restricted by
$(x,y)$
coordinates are restricted by
which is the extent of the Kelvin wake region. Along the cusp line (2.5) is satisfied for
![]() ${\it\theta}_{s}={\it\phi}_{P}$
, whereas two distinct angles will satisfy (2.5) for points within the Kelvin wedge: a value
${\it\theta}_{s}={\it\phi}_{P}$
, whereas two distinct angles will satisfy (2.5) for points within the Kelvin wedge: a value
![]() ${\it\theta}_{s}<{\it\phi}_{P}$
corresponding to the transverse wake wave component and a value
${\it\theta}_{s}<{\it\phi}_{P}$
corresponding to the transverse wake wave component and a value
![]() ${\it\theta}_{s}>{\it\phi}_{P}$
corresponding to the divergent wake wave component. Hence, the value of
${\it\theta}_{s}>{\it\phi}_{P}$
corresponding to the divergent wake wave component. Hence, the value of
![]() ${\it\theta}_{s}$
also determines the value of
${\it\theta}_{s}$
also determines the value of
![]() ${\it\xi}$
to be used in (2.3).
${\it\xi}$
to be used in (2.3).
Figure 4 shows the spectrogram of the far-field wake using the approximation defined by (2.3)–(2.5), for two different ship speeds (
![]() $U=5.0~\text{m}~\text{s}^{-1}$
and
$U=5.0~\text{m}~\text{s}^{-1}$
and
![]() $U=10.0~\text{m}~\text{s}^{-1}$
) at three observation points at distances of
$U=10.0~\text{m}~\text{s}^{-1}$
) at three observation points at distances of
![]() $Y=1$
, 2 and 4 km from the sailing line. The source amplitude function in (2.3) has in this case been assigned a constant value
$Y=1$
, 2 and 4 km from the sailing line. The source amplitude function in (2.3) has in this case been assigned a constant value
![]() $A({\it\theta})=1~\text{m}$
. The spectrogram shows two strong signals: a slanting chirp, corresponding to the diverging wake component, and a nearly horizontal line (almost monochromatic wave), corresponding to the transverse wake component (figure 1).
$A({\it\theta})=1~\text{m}$
. The spectrogram shows two strong signals: a slanting chirp, corresponding to the diverging wake component, and a nearly horizontal line (almost monochromatic wave), corresponding to the transverse wake component (figure 1).

Figure 5. Spectrograms for 24 h wave records at (a) Aegna (09/07/2008) and (b) Pikakari (29/06/2009). The original wave measurement time series is plotted above each spectrogram panel.
Figure 4 demonstrates that a change in speed corresponds to a shift in wave frequency, with lower-frequency waves being generated when the speed of the source is higher. The increase in distance to the observation point has little impact on the transversal wake component, but changes the chirp angle for the divergent wake. This is a natural response to the wave dispersion, since the high-frequency waves travel slower than low-frequency waves. Therefore this slanting angle can be used as an indicator of the distance between the wave source and the observation point.
2.2.2. Ship speed and distance to ship sailing line
Assuming that the ship passing the measurement site is travelling along a straight line and with constant speed, its speed
![]() $U$
can be estimated from the spectrogram using either the divergent or the transversal wave signals. If the starting point frequency (lowest frequency) of the chirp signal (diverging wake system) is well defined in the spectrogram, it is reasonable to assume that it represents the frequency of the cusp waves, and the speed of the ship can then be calculated using the deep-water relation (2.2):
$U$
can be estimated from the spectrogram using either the divergent or the transversal wave signals. If the starting point frequency (lowest frequency) of the chirp signal (diverging wake system) is well defined in the spectrogram, it is reasonable to assume that it represents the frequency of the cusp waves, and the speed of the ship can then be calculated using the deep-water relation (2.2):
Note that
![]() ${\it\phi}_{P}$
is here defined specifically as the angle of propagation for the cusp wave system as obtained from Kelvin wake theory. As mentioned in the introduction, factors such as water depth, shear flow or nonlinear wave interaction may alter the wake pattern, hence the dominating waves in wake measurements may propagate at a different angle. Alternatively, the speed could be estimated using the frequency of the transverse waves along the sailing line
${\it\phi}_{P}$
is here defined specifically as the angle of propagation for the cusp wave system as obtained from Kelvin wake theory. As mentioned in the introduction, factors such as water depth, shear flow or nonlinear wave interaction may alter the wake pattern, hence the dominating waves in wake measurements may propagate at a different angle. Alternatively, the speed could be estimated using the frequency of the transverse waves along the sailing line
i.e. waves for which
![]() ${\it\theta}=0^{\circ }$
. In principle these waves will never reach a measurement point that is located adjacent to the sailing line, but in practice the estimate should be fairly robust provided that a distinct transverse wave signal can be identified in the spectrogram. For example, at the Kelvin wake half-angle
${\it\theta}=0^{\circ }$
. In principle these waves will never reach a measurement point that is located adjacent to the sailing line, but in practice the estimate should be fairly robust provided that a distinct transverse wave signal can be identified in the spectrogram. For example, at the Kelvin wake half-angle
![]() ${\it\alpha}=10^{\circ }$
the transverse waves propagate at an angle
${\it\alpha}=10^{\circ }$
the transverse waves propagate at an angle
![]() ${\it\theta}_{T}=10.7^{\circ }$
, which gives the relation between the ship speed and wave frequency
${\it\theta}_{T}=10.7^{\circ }$
, which gives the relation between the ship speed and wave frequency
hence the error of the estimate of
![]() $U$
given by (2.8) is less than 2 % for waves along this line. Furthermore, the results of (2.7) and (2.8) differ by
$U$
given by (2.8) is less than 2 % for waves along this line. Furthermore, the results of (2.7) and (2.8) differ by
![]() $\sqrt{3/2}$
, i.e. approximately 22 %.
$\sqrt{3/2}$
, i.e. approximately 22 %.
If the spectrogram provides information about both the frequency of the cusp waves and speed of the ship, the distance to the sailing line can also be estimated. To determine the distance in question, it is sufficient to specify the time instant at which point
![]() $Q$
of the wake system arrives. This point corresponds to the frequency
$Q$
of the wake system arrives. This point corresponds to the frequency
![]() $f_{Q}$
of diverging waves. The frequency of the diverging waves at points
$f_{Q}$
of diverging waves. The frequency of the diverging waves at points
![]() $P$
and
$P$
and
![]() $Q$
(figure 3) is given from (2.2) by
$Q$
(figure 3) is given from (2.2) by
with
![]() ${\it\phi}_{Q}=90^{\circ }-{\it\phi}_{P}$
, hence the relation between these frequencies is
${\it\phi}_{Q}=90^{\circ }-{\it\phi}_{P}$
, hence the relation between these frequencies is
If the frequency
![]() $f_{P}$
is observed at time
$f_{P}$
is observed at time
![]() $t_{1}$
and waves of frequency
$t_{1}$
and waves of frequency
![]() $f_{Q}$
arrive at time
$f_{Q}$
arrive at time
![]() $t_{2}$
, the distance
$t_{2}$
, the distance
![]() $L$
between points
$L$
between points
![]() $P$
and
$P$
and
![]() $B$
is
$B$
is
From a management point of view it is easier to relate wake properties with the shortest distance to the sailing line
since most ship speed restrictions in coastal waters are defined in terms of distance from shore.
2.3. Analysis of measurement data
For the time–frequency analysis of the observations of sea-surface elevation, time series were divided into 24 h segments, that were de-meaned and filtered (by subtracting a 2 min running average) to remove low-frequency (10 min time scale) water-level fluctuations (see Soomere, Parnell & Didenkulova Reference Soomere, Parnell and Didenkulova2011 for the necessity of this operation). The filtered time series was analysed using the short-time Fourier decomposition (MATLAB spectrogram function), with 180 s Hemming windows (900 data points sampled at 5 Hz) and 170 s window overlap, resulting in a spectrogram with a time–frequency resolution of
![]() $10~\text{s}\times 0.005~\text{Hz}$
and a frequency range of 0.005–0.6 Hz (figure 5). The power spectral density
$10~\text{s}\times 0.005~\text{Hz}$
and a frequency range of 0.005–0.6 Hz (figure 5). The power spectral density
![]() $S({\it\tau},f)$
was plotted using a colour scale of
$S({\it\tau},f)$
was plotted using a colour scale of
![]() $\log _{10}S$
, where
$\log _{10}S$
, where
![]() ${\it\tau}$
is time. Results obtained using windowed Fourier analysis and Morlet-based wavelet analysis were consistent; however, the former method was preferred for its uniform frequency resolution.
${\it\tau}$
is time. Results obtained using windowed Fourier analysis and Morlet-based wavelet analysis were consistent; however, the former method was preferred for its uniform frequency resolution.

Figure 6. Examples of wake measurements: (a–c) at Aegna; (d–f) at Pikakari. Panels are annotated according to the source of the most prominent wake event within the 1 h time slot shown: (a,d) Star; (b,e) Superstar; (c, f) Viking XPRS. In (c) the wake signal for Viking XPRS starts approximately at 18:35. Plots (a–d) were published in Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013), and are here reproduced with permission from Journal of Coastal Research.
The 24 h spectrograms in figure 5 show results for the two measurement sites on days with calm or moderate wind wave conditions. The chirp (sliding frequency) signal associated with ship wakes can easily be identified in the records as slanting linear features, whereas the background wind conditions produce a wide-banded signal, usually at higher frequencies than the main part of the ship wake signal. As overlapping ship wakes occur frequently, the identification of a single wake event is difficult. It is therefore also difficult to formulate an automatic identification algorithm for the detection of ship wake events, and we have instead relied on manual treatment of each wake event in the following analysis.
3. Results
In the analysis of wake records we focused on wakes generated by three ships (Star, Superstar and Viking XPRS), which regularly passed near the measurement sites (see Parnell et al.
Reference Parnell, Delpeche, Didenkulova, Dolphin, Erm, Kask, Kelpšaite, Kurennoy, Quak, Räämet, Soomere, Terentjeva, Torsvik and Zaitseva-Pärnaste2008). The three mentioned ships are of similar size (
![]() $L_{s}\sim 175{-}186~\text{m}$
) and similar maximum operation speed (
$L_{s}\sim 175{-}186~\text{m}$
) and similar maximum operation speed (
![]() $U\sim 12.8{-}14.2~\text{m}~\text{s}^{-1}$
), and are responsible for some of the highest wave loads on the coast (Didenkulova & Soomere Reference Didenkulova and Soomere2011). The length Froude number is therefore not very large for these ships,
$U\sim 12.8{-}14.2~\text{m}~\text{s}^{-1}$
), and are responsible for some of the highest wave loads on the coast (Didenkulova & Soomere Reference Didenkulova and Soomere2011). The length Froude number is therefore not very large for these ships,
![]() $F_{L}\lesssim 0.34$
. The water depth along parts of the sailing line lies between 20 and 40 m, particularly for north-bound ships, hence the depth Froude number can potentially be in the range
$F_{L}\lesssim 0.34$
. The water depth along parts of the sailing line lies between 20 and 40 m, particularly for north-bound ships, hence the depth Froude number can potentially be in the range
![]() $F_{d}\sim 0.72{-}1.0$
within these regions (Torsvik et al.
Reference Torsvik, Didenkulova, Soomere and Parnell2009). The analysis presented here focuses on single events that could be reasonably identified and that occurred on days with little wind-wave background.
$F_{d}\sim 0.72{-}1.0$
within these regions (Torsvik et al.
Reference Torsvik, Didenkulova, Soomere and Parnell2009). The analysis presented here focuses on single events that could be reasonably identified and that occurred on days with little wind-wave background.
3.1. Identification of ship wake structures
Figure 6 show examples of wake waves and corresponding spectrograms at the two measurement sites. Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013) discussed the characteristic properties of these signals as they appeared in the time–frequency space. However, the relationship between the spectrogram structures and the wake components was not properly recognized at the time, and it is therefore necessary to re-evaluate the interpretation of the spectrograms in the light of the structures found for the classical Kelvin wake system (§ 2.2, figure 4). Specifically, it was not recognized in Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013) that the divergent wave components were the cause of the slanting chirp signal which is a distinct feature for both the theoretical (figure 4) and measured (figure 6) wake patterns.
For the transversal waves the angle
![]() ${\it\theta}$
is at maximum (approximately 35.3° in deep water) at the instant of arrival of the cusp line and decreases to zero when the ship is infinitely far away. The signal of transverse waves should thus be located in a narrow frequency range that varies by less than 20 %. Despite the background noise due to wind generated waves and overlapping wake signals, there is a clear resemblance between the measured spectrogram representations in figure 6 and the idealized Kelvin wake representation in figure 4, indicating that the transverse and divergent wake components can be identified fairly reliably by this method. These features are illustrated well in figure 6( f) for the wake signal of Viking XPRS measured at Pikakari Beach.
${\it\theta}$
is at maximum (approximately 35.3° in deep water) at the instant of arrival of the cusp line and decreases to zero when the ship is infinitely far away. The signal of transverse waves should thus be located in a narrow frequency range that varies by less than 20 %. Despite the background noise due to wind generated waves and overlapping wake signals, there is a clear resemblance between the measured spectrogram representations in figure 6 and the idealized Kelvin wake representation in figure 4, indicating that the transverse and divergent wake components can be identified fairly reliably by this method. These features are illustrated well in figure 6( f) for the wake signal of Viking XPRS measured at Pikakari Beach.
It is notable that the branches corresponding to transversal and divergent wave trains do not have the same duration. This is probably due to specific geometrical properties of the bay (bathymetry and coastline configuration) and the difference in the ferry speed along the ship tracks (Torsvik et al. Reference Torsvik, Didenkulova, Soomere and Parnell2009). The southern part of Tallinn Bay is shallow, and ferries are not able to navigate in this region at full speed, which also reduces their capability to generate large wake waves in this part of the bay. This may account for the relatively short transversal wake signal at the Aegna measurement site. In contrast, ferries approaching Tallinn from the north maintain full speed far into the bay, moving from deep to shallow water. As a consequence, the transversal component of wakes from southbound ferries measured at Pikakari Beach has a much longer duration than for the same ships moving northward measured at Aegna.
In the Kelvin wake theory the transverse and divergent wake components are shifted in phase by 90° along the cusp line (Newman Reference Newman1977). Furthermore, the Kelvin wake wave pattern is correct only for the wake generated by a moving point source. A more realistic model should take into account several pressure sources along the ship hull, in particular the bow and stern wave systems. It is therefore to be expected that the cusp wave system does not correspond to a sharply defined single wave frequency. However, in most recorded wake signals a well-defined peak in the spectrogram corresponds to the arrival of the leading large-amplitude wave group. Higher harmonics of the main frequency are also apparent in the wakes of Star and Superstar (figure 6). At the arrival time of the cusp waves, the wave energy has quite a wide spectrum, in particular at Aegna (figure 6 a,b), which corresponds to nonlinear effects within the shallow-water framework. Since our waves are influenced by shallow-water effects, they become asymmetric during their propagation with a substantial steepening of the wavefront, which leads to the generation of higher harmonics and therefore widening of the wave spectrum (Zahibo et al. Reference Zahibo, Didenkulova, Kurkin and Pelinovsky2008). Although we cannot be sure about the source of this nonlinearity, possible mechanisms include the classical deformation of wave shape in shallow water (Didenkulova et al. Reference Didenkulova, Zahibo, Kurkin and Pelinovsky2006, Reference Didenkulova, Parnell, Soomere, Pelinovsky and Kurennoy2009), or nonlinear wave components travelling with the cusp wave system as bound modes.
In the wake signals for Star and Superstar at Aegna (figure 6 a,b), part of the wake energy arrives prior to the largest waves (Soomere Reference Soomere2007). This feature appears in the low-frequency range of the spectrogram, and is likely to be an indication of precursor solitary waves. Such features are know to occur in the wakes of ships moving at high speed in shallow water (Wu Reference Wu1987; Neuman et al. Reference Neuman, Tapio, Haggard, Laws and Bland2001).
To investigate the persistence of the wake structure for different ships at the two measurement sites, we extract characteristic features of the wake from the spectrograms. The panels in figure 7 present the local peaks in spectrograms (single points in the time–frequency space) for several wake events. The points corresponding to different wakes from the same ship are plotted with different colours, and aligned in time with respect to the first occurrence of a peak value at a specific frequency, depending on the data available for each of the wake signals. This procedure relies heavily on the judgment of the investigator in extracting all peak values that are part of the wake signal, and removing similar values corresponding to background noise or wakes from other ships. Therefore figure 7 may not be exactly reproducible, and may contain features that are not part of the wake signal, or lack features that should be included in the wake signal. This is particularly the case for wakes from Viking XPRS at Aegna (figure 7 c). This vessel departed from Tallinn at times of heavy ship traffic in the bay, resulting in relatively short time windows without overlapping wake signals. The main features of the wakes become apparent if we assume that the clustering of points from many wakes into single lines corresponds to persistent components of the wake. In particular, the transverse and divergent wake features for Pikakari Beach are clearly defined in figure 7(d–f).

Figure 7. Superposition of peak spectrogram values for several wake events generated by a single vessel: (a,d) Star; (b,e) Superstar; (c, f) Viking XPRS. Points with different colours represent peak values for different wake events. (a–c) Measurements at Aegna; (d–f) measurements at Pikakari.
3.2. The sailing speed
Figure 8 demonstrate that the characteristic wake features are essentially the same for Star and Superstar. The frequency of the transversal waves is slightly higher for Viking XPRS than for the two other ships, indicating that this ship is moving slower (as demonstrated for the Kelvin wake in figure 4). The chirp lines corresponding to the divergent waves appear to be parallel, indicating that the three ships passed the observation point at the same distance.

Figure 8. Structure of ship wakes measured at (a) Aegna and (b) Pikakari, extracted from peak value analysis of spectrograms in figure 7.
As shown in § 2.2.2, the key parameter for calculation of the ship speed
![]() $U$
and distance between measurement point and ship line
$U$
and distance between measurement point and ship line
![]() $Y$
is the frequency of the cusp wave system
$Y$
is the frequency of the cusp wave system
![]() $f_{P}$
. However, it is not always straightforward to obtain this value directly by inspection of spectrograms, as demonstrated in figure 8. The plots have been normalized so that the cusp wave system is present at approximately
$f_{P}$
. However, it is not always straightforward to obtain this value directly by inspection of spectrograms, as demonstrated in figure 8. The plots have been normalized so that the cusp wave system is present at approximately
![]() $t=0~\text{s}$
. At this time instant a strong signal with quite a wide spectrum arrives, especially in the case of the Star and Superstar. Here we propose three different methods that can be used to obtain an estimate for
$t=0~\text{s}$
. At this time instant a strong signal with quite a wide spectrum arrives, especially in the case of the Star and Superstar. Here we propose three different methods that can be used to obtain an estimate for
![]() $f_{P}$
, which also determines the ship speed
$f_{P}$
, which also determines the ship speed
![]() $U$
.
$U$
.
Note that the theory presented in § 2.2.2 is based on linear deep-water theory, whereas the ship wakes discussed in this paper contain considerable shallow-water effects and large values of
![]() $F_{d}$
. However, analysis of wakes based on shallow-water theory requires knowledge of the depth Froude number, but in this paper we assume that no information regarding the wave source is available. Therefore we use the deep-water assumption which does not require knowledge of water depth and ship speed at the generation point, and thereafter check the accuracy of the obtained results.
$F_{d}$
. However, analysis of wakes based on shallow-water theory requires knowledge of the depth Froude number, but in this paper we assume that no information regarding the wave source is available. Therefore we use the deep-water assumption which does not require knowledge of water depth and ship speed at the generation point, and thereafter check the accuracy of the obtained results.
The first method (A) uses the frequency of the maximum spectrogram value
![]() $f(S_{max})$
as an indicator for the dominant frequency within the cusp wave system. These values were presented in Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013) (table 1 in that paper), and are included here in the first column of table 1. In Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013) it was suggested that the maximum spectrogram value
$f(S_{max})$
as an indicator for the dominant frequency within the cusp wave system. These values were presented in Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013) (table 1 in that paper), and are included here in the first column of table 1. In Didenkulova et al. (Reference Didenkulova, Sheremet, Torsvik and Soomere2013) it was suggested that the maximum spectrogram value
![]() $S_{max}$
and its frequency
$S_{max}$
and its frequency
![]() $f(S_{max})$
could be used to characterize wakes from different ships. Further analysis has revealed that these maxima mostly coincide with the arrival of the cusp wave system, hence it is reasonable to assume that the frequency is indicative of the cusp wave frequency
$f(S_{max})$
could be used to characterize wakes from different ships. Further analysis has revealed that these maxima mostly coincide with the arrival of the cusp wave system, hence it is reasonable to assume that the frequency is indicative of the cusp wave frequency
![]() $f_{P}$
. In this case the ship speed
$f_{P}$
. In this case the ship speed
![]() $U$
can be calculated directly from (2.7).
$U$
can be calculated directly from (2.7).
Table 1. Cusp line frequencies and corresponding ship speed estimates. Superscripts (A), (B) and (C) correspond to the respective method used to obtain the frequency and speed estimates. The reference speed
![]() $U_{ref}$
is the average operating speed of each vessel (Parnell et al.
Reference Parnell, Delpeche, Didenkulova, Dolphin, Erm, Kask, Kelpšaite, Kurennoy, Quak, Räämet, Soomere, Terentjeva, Torsvik and Zaitseva-Pärnaste2008). Note that the operating speed
$U_{ref}$
is the average operating speed of each vessel (Parnell et al.
Reference Parnell, Delpeche, Didenkulova, Dolphin, Erm, Kask, Kelpšaite, Kurennoy, Quak, Räämet, Soomere, Terentjeva, Torsvik and Zaitseva-Pärnaste2008). Note that the operating speed
![]() $U_{ref}$
does not represent the actual speed of the ship in the Tallinn Bay region, but can be treated as an upper bound for the ship speed in coastal regions.
$U_{ref}$
does not represent the actual speed of the ship in the Tallinn Bay region, but can be treated as an upper bound for the ship speed in coastal regions.

The second method (B) makes use of the divergent wake structure (chirp signal), and identifies
![]() $f_{P}$
as the frequency of the chirp signal at
$f_{P}$
as the frequency of the chirp signal at
![]() $t=0~\text{s}$
in figure 8. To obtain a single frequency at the
$t=0~\text{s}$
in figure 8. To obtain a single frequency at the
![]() $t=0~\text{s}$
intersection, we have applied a least squares linear fit to the chirp line data. Having obtained the
$t=0~\text{s}$
intersection, we have applied a least squares linear fit to the chirp line data. Having obtained the
![]() $f_{P}$
value, we again make use of (2.7) to obtain the ship speed (see table 1).
$f_{P}$
value, we again make use of (2.7) to obtain the ship speed (see table 1).
The third method (C) makes use of the transversal wake component. Proceeding as with method (B), we apply a least squares quadratic fit of the transverse chirp signal from
![]() $t=0~\text{s}$
until the end of the recorded data, and use the mean frequency
$t=0~\text{s}$
until the end of the recorded data, and use the mean frequency
![]() $f$
of this curve as the indicator for the transverse wave component. In this case we calculate the ship speed from (2.8), and obtain the corresponding cusp line frequency
$f$
of this curve as the indicator for the transverse wave component. In this case we calculate the ship speed from (2.8), and obtain the corresponding cusp line frequency
![]() $f_{P}$
from (2.10). This procedure requires a clearly defined transversal branch, and it is therefore not applicable for Viking XPRS at Aegna, where a single branch could not be identified (figure 8
a).
$f_{P}$
from (2.10). This procedure requires a clearly defined transversal branch, and it is therefore not applicable for Viking XPRS at Aegna, where a single branch could not be identified (figure 8
a).
The ship speed
![]() $U^{(A)}$
(table 1) calculated with method (A) seems to be severely overestimated for Star and Superstar at Aegna, and slightly overestimated for Pikakari Beach. A possible reason may be an increase of the wake wedge angle
$U^{(A)}$
(table 1) calculated with method (A) seems to be severely overestimated for Star and Superstar at Aegna, and slightly overestimated for Pikakari Beach. A possible reason may be an increase of the wake wedge angle
![]() ${\it\alpha}$
at high
${\it\alpha}$
at high
![]() $F_{d}\gtrsim 0.7$
. However,
$F_{d}\gtrsim 0.7$
. However,
![]() $U^{(A)}$
is closer to the reference value
$U^{(A)}$
is closer to the reference value
![]() $U_{ref}$
than the two other estimates for Viking XPRS. It should be noted that the ships generally accelerate prior to reaching Aegna, whereas they maintain a nearly constant speed prior to reaching Pikakari Beach (Torsvik et al.
Reference Torsvik, Didenkulova, Soomere and Parnell2009), hence it is reasonable to assume that the estimates in table 1 are more reliable for Pikakari Beach than for Aegna. This gradual change in sailing speed explains why the transversal branches for Star and Superstar at Aegna are gradually increasing in frequency over time (figure 8
a), while the equivalent branches for Pikakari Beach have almost a constant frequency (figure 8
b).
$U_{ref}$
than the two other estimates for Viking XPRS. It should be noted that the ships generally accelerate prior to reaching Aegna, whereas they maintain a nearly constant speed prior to reaching Pikakari Beach (Torsvik et al.
Reference Torsvik, Didenkulova, Soomere and Parnell2009), hence it is reasonable to assume that the estimates in table 1 are more reliable for Pikakari Beach than for Aegna. This gradual change in sailing speed explains why the transversal branches for Star and Superstar at Aegna are gradually increasing in frequency over time (figure 8
a), while the equivalent branches for Pikakari Beach have almost a constant frequency (figure 8
b).
3.3. The distance from the ship sailing line
The distance from the ship sailing lane to the measurement site can be calculated using reliable estimates for the ship speed
![]() $U$
and cusp wave frequency
$U$
and cusp wave frequency
![]() $f_{P}$
, and the time lag between arrivals of the cusp wave frequency and the frequency
$f_{P}$
, and the time lag between arrivals of the cusp wave frequency and the frequency
![]() $f_{Q}$
defined by (2.11). If measurement of
$f_{Q}$
defined by (2.11). If measurement of
![]() $f_{P}$
is normalized to
$f_{P}$
is normalized to
![]() $t_{1}=0~\text{s}$
(figure 8), the time
$t_{1}=0~\text{s}$
(figure 8), the time
![]() $t_{2}$
is found as the intersection of the chirp signal with
$t_{2}$
is found as the intersection of the chirp signal with
![]() $f_{Q}=\sqrt{2}f_{P}$
. In order to minimize the influence of noise for the identification of
$f_{Q}=\sqrt{2}f_{P}$
. In order to minimize the influence of noise for the identification of
![]() $t_{2}$
, we have again applied the least squares linear fit to the chirp line data, as described for method (B) above, and search for the
$t_{2}$
, we have again applied the least squares linear fit to the chirp line data, as described for method (B) above, and search for the
![]() $f_{Q}$
frequency along this line. This provides sufficient information to calculate the travel distance
$f_{Q}$
frequency along this line. This provides sufficient information to calculate the travel distance
![]() $L$
for the cusp wave system from (2.12), or the distance to the shipping lane
$L$
for the cusp wave system from (2.12), or the distance to the shipping lane
![]() $Y$
from (2.13).
$Y$
from (2.13).
Table 2. Estimated distance between the ship travel line and the measurement site. Superscripts (A), (B) and (C) correspond to the respective values for
![]() $f_{P}$
and
$f_{P}$
and
![]() $U$
from table 1 used in the calculation of the distance
$U$
from table 1 used in the calculation of the distance
![]() $Y$
. The reference distance
$Y$
. The reference distance
![]() $Y_{ref}$
applies to all three ships, and is based on distance measured during field experiments.
$Y_{ref}$
applies to all three ships, and is based on distance measured during field experiments.

Table 2 shows estimates for the distance from the ship lane to the measurement site. No estimate was obtained for Star at Aegna, because the frequency
![]() $f_{Q}^{(A)}=0.150~\text{Hz}$
corresponding to
$f_{Q}^{(A)}=0.150~\text{Hz}$
corresponding to
![]() $f_{P}^{(A)}$
, was equivalent to the starting frequency for the chirp signal. In general, the results obtained by method (A) underestimate the distance
$f_{P}^{(A)}$
, was equivalent to the starting frequency for the chirp signal. In general, the results obtained by method (A) underestimate the distance
![]() $Y$
, whereas methods (B) and (C) slightly overestimate this value. The ships follow the same route when approaching and leaving Tallinn, so the values for the different ships can be considered as independent estimates of the same distance. Using the more reliable Pikakari Beach results, and taking the average of the three estimates, we find that
$Y$
, whereas methods (B) and (C) slightly overestimate this value. The ships follow the same route when approaching and leaving Tallinn, so the values for the different ships can be considered as independent estimates of the same distance. Using the more reliable Pikakari Beach results, and taking the average of the three estimates, we find that
![]() $Y^{(A)}$
underestimates
$Y^{(A)}$
underestimates
![]() $Y_{ref}$
by 66 %, whereas
$Y_{ref}$
by 66 %, whereas
![]() $Y^{(B)}$
and
$Y^{(B)}$
and
![]() $Y^{(C)}$
overestimate
$Y^{(C)}$
overestimate
![]() $Y_{ref}$
by 117 % and 122 %, respectively. For Aegna, a similar averaging using the available results, and a reference distance of
$Y_{ref}$
by 117 % and 122 %, respectively. For Aegna, a similar averaging using the available results, and a reference distance of
![]() $Y_{ref}=2.75$
km, gives an underestimation of
$Y_{ref}=2.75$
km, gives an underestimation of
![]() $Y_{ref}$
by 45 % and an overestimation of
$Y_{ref}$
by 45 % and an overestimation of
![]() $Y^{(B)}$
and
$Y^{(B)}$
and
![]() $Y^{(C)}$
by 132 % and 167 %, respectively. Hence, the procedure outlined as method (B) appears to give the best results overall.
$Y^{(C)}$
by 132 % and 167 %, respectively. Hence, the procedure outlined as method (B) appears to give the best results overall.
4. Energy related to different wake components
Analysis of the wave energy contained in the different wake signals has previously been discussed for the Aegna experiment (Parnell et al. Reference Parnell, Delpeche, Didenkulova, Dolphin, Erm, Kask, Kelpšaite, Kurennoy, Quak, Räämet, Soomere, Terentjeva, Torsvik and Zaitseva-Pärnaste2008) and Pikakari Beach experiment (Kurennoy et al. Reference Kurennoy, Parnell and Soomere2011). The spectrogram representation allows a more detailed analysis of the wake energy, and in particular the decomposition of the wake into components of different nature and an examination of the contribution from each individual component.
The procedure of wake decomposition and energy analysis is illustrated in figure 9. The first step is to identify regions within the spectrogram that correspond to different wake features. In this case we have decomposed the wake into five components: leading waves (LW), the divergent wake component (DW), the transverse wake component (TW), precursor solitary waves (PW), and low-frequency disturbances (LF) coinciding with the wake event. These areas are marked by white dashed lines in the spectrogram figure 9(a). The total wake event is confined to a 40 min time window, and each component area is defined in units of 5 min time slices to enable a straightforward comparison between wake events. The frequency range is limited to 0–0.4 Hz, which avoids interference with background noise (BN), but arguably also disregards some wake energy in the high-frequency range. In addition to the five wake components we select a 5 min time window that contains minimal wake noise. The wave field in this slice is assumed to represent the background wind wave component in the spectrogram. It is natural to assume that this background is approximately stationary within the typical duration of the wake. These wind wave background data are converted to a gently varying power spectral density wind wave profile
![]() $S_{\mathit{wind}}$
by averaging in time and applying a low-pass filter to smooth the profile over the chosen frequency range. The power spectral density for each wake component is then extracted as
$S_{\mathit{wind}}$
by averaging in time and applying a low-pass filter to smooth the profile over the chosen frequency range. The power spectral density for each wake component is then extracted as
which avoids negative
![]() $S$
values when removing the background wind wave component.
$S$
values when removing the background wind wave component.

Figure 9. Wake energy analysis for Star at Aegna. Wave energy is calculated for the area enclosed by the black stippled lines. The original spectrogram (a) is decomposed into five segments, marked by white dashed lines, representing different wake components. A reference wind wave background is taken from the area enclosed by the red dashed line. Plot (b) shows the five segments of the decomposition, where line plots along the
![]() $x$
-axis and
$x$
-axis and
![]() $y$
-axis show the time- and frequency-integrated profiles, respectively.
$y$
-axis show the time- and frequency-integrated profiles, respectively.
The wake energy is computed over the 40 min time series directly from the original water level measurement
![]() ${\it\eta}(t)$
from the integral
${\it\eta}(t)$
from the integral
where
![]() ${\it\rho}$
is the density of water,
${\it\rho}$
is the density of water,
![]() $T_{0}$
is the start time of the measurement and
$T_{0}$
is the start time of the measurement and
![]() $T_{w}$
is the duration of the time window. This is equivalent to the energy content of the spectrogram, which is calculated by integrating over time and frequency, and where
$T_{w}$
is the duration of the time window. This is equivalent to the energy content of the spectrogram, which is calculated by integrating over time and frequency, and where
![]() ${\it\kappa}$
is a constant that depends on the physical parameters. The energy content of each wake component is computed by
${\it\kappa}$
is a constant that depends on the physical parameters. The energy content of each wake component is computed by
The total wake energy is calculated as the sum of the energy of the five wake components, and the wind wave field contribution is calculated based on the wind wave background profile content within the same five wake component regions in the spectrogram. The remaining energy within the 40 min time window is regarded as background noise, either due to wind wave input in the high-frequency range, or as in the example in figure 9, due to the energy from previous wake events. In order to have a reliable result it is desirable that the background noise and wind wave field components are small compared to the total wake energy. It is also possible to have reliable results even if the background noise level is relatively high, but the results will be highly questionable if the wind wave field component is large relative to the total wake energy.
Figure 10 shows a histogram of the wave energy for different ship wake components in figure 9, calculated by the procedure outlined above. The total wave energy (Tot) is calculated first by (4.2), then the energy content of the five wake components is calculated by (4.3), and the sum of these components gives the total ship wake energy (SW) for this wake event. The histogram also includes the wind wave (WW) energy extracted from the five wake component regions, and the background noise (BN) energy level which has been calculated as

Figure 10. The energy of the different wake components in figure 9. The labels on the
![]() $x$
-axis correspond to Tot: total wave energy; BN: background noise; WW: wind wave field; SW: total ship wake energy; LW: leading waves; DW: divergent wake component; TW: transverse wake component; PW: precursor solitary waves; LF: low-frequency disturbances. Values on the left-hand
$x$
-axis correspond to Tot: total wave energy; BN: background noise; WW: wind wave field; SW: total ship wake energy; LW: leading waves; DW: divergent wake component; TW: transverse wake component; PW: precursor solitary waves; LF: low-frequency disturbances. Values on the left-hand
![]() $y$
-axis are the time-integrated energy per unit area, and the right-hand
$y$
-axis are the time-integrated energy per unit area, and the right-hand
![]() $y$
-axis indicates percentage of the total ship wake energy (SW).
$y$
-axis indicates percentage of the total ship wake energy (SW).
The wake energy analysis has only been carried out for wakes from Star and Superstar, treating these as equivalent. Viking XPRS wake events have not been analysed due to the problem of finding ‘clean’ wake measurements. Table 3 shows the average and standard deviation for the Star and Superstar wakes at Aegna and Pikakari Beach. The total wake energy levels are higher than what was reported for Aegna measurements by Parnell et al. (Reference Parnell, Delpeche, Didenkulova, Dolphin, Erm, Kask, Kelpšaite, Kurennoy, Quak, Räämet, Soomere, Terentjeva, Torsvik and Zaitseva-Pärnaste2008), who reported average energy levels for Star and Superstar at
![]() $4.9\times 10^{4}~\text{J}~\text{s}~\text{m}^{-2}$
and
$4.9\times 10^{4}~\text{J}~\text{s}~\text{m}^{-2}$
and
![]() $6.6\times 10^{4}~\text{J}~\text{s}~\text{m}^{-2}$
, respectively. This can easily be explained by the wake duration, which is twice the length in our analysis compared to the previous study. The same comment applies to the comparison with the previous wake energy analysis for the Pikakari Beach measurements by Kurennoy et al. (Reference Kurennoy, Parnell and Soomere2011), who reported average energy levels for Star and Superstar at
$6.6\times 10^{4}~\text{J}~\text{s}~\text{m}^{-2}$
, respectively. This can easily be explained by the wake duration, which is twice the length in our analysis compared to the previous study. The same comment applies to the comparison with the previous wake energy analysis for the Pikakari Beach measurements by Kurennoy et al. (Reference Kurennoy, Parnell and Soomere2011), who reported average energy levels for Star and Superstar at
![]() $2.0\times 10^{4}~\text{J}~\text{s}~\text{m}^{-2}$
and
$2.0\times 10^{4}~\text{J}~\text{s}~\text{m}^{-2}$
and
![]() $3.3\times 10^{4}~\text{J}~\text{s}~\text{m}^{-2}$
, respectively. In both these cases the spectrogram analysis has revealed that the wake energy is present for a much longer duration than previously realized, and that previous estimates for the wake energy may have been underestimated by as much as 50 %.
$3.3\times 10^{4}~\text{J}~\text{s}~\text{m}^{-2}$
, respectively. In both these cases the spectrogram analysis has revealed that the wake energy is present for a much longer duration than previously realized, and that previous estimates for the wake energy may have been underestimated by as much as 50 %.
Table 3. Wake energy distribution for Star and Superstar.

The new element in the wake energy analysis, when compared to previous studies, is the possibility of extracting the wake energy contribution for different wake components. In table 3 the contributions for different components are shown as a percentage of the total wake energy, with standard deviation in percentage points. For Aegna the leading wave system contributes over 80 % of the total wake energy, and the main low-frequency contribution is associated with the precursor wave system. At Pikakari Beach, although the leading wave system dominates by contributing around 60 % of the wake energy, far more of the wake energy is distributed in the long lasting tail of the wake. Also, while there is almost no indication of a precursor wave system at this location, a substantial amount of wave energy is present in the low-frequency range after the impact of the leading wave system, in this way adding hydrodynamic loads to the nearshore ecosystem and coastal processes.
Note that the energy analysis presented above is integrated over 5 min intervals and is related to wave groups. Specifically for the leading wave system it therefore is not possible to resolve the contribution from individual waves. The leading wave system contains contribution from the cusp wave system, but probably also elements of transverse and divergent waves, and it is not possible to quantify their contributions more specifically using this analysis.
5. Discussion and concluding remarks
Recent research (Rabaud & Moisy Reference Rabaud and Moisy2013; Darmon et al. Reference Darmon, Benzaquen and Raphael2014) has highlighted the complexity of the ship wake structure and demonstrated that the appearance and properties of even the (formally) Kelvin wake may substantially change at higher Froude numbers. Our analysis shows that remarkable differences of the actual wake patterns from the ideal linear Kelvin wakes exist even at relatively low Froude numbers. These differences, as well as the presence, duration and certain properties of different components of the wake, can be effectively highlighted in our case even when the ships sail at clearly subcritical speeds. In particular, figure 9 can be interpreted as showing that the highest waves occur in the interior of the wake wedge (although quite close to the edge of this wedge).
The spectrogram analysis makes it possible to estimate the ship speed and the wake travel distance between its place of origin (sailing line) and the measurement site. Crucially, the estimate does not need any prior knowledge of where the typical sailing line is located. It uses exclusively the information available within the record of surface elevation and fundamentals of the Kelvin wake theory. The key tool is the transformation of this information into a geometric representation of the chirp-like signals of the classical components (diverging and transversal waves) of the Kelvin wake. The simple estimate presented here strongly relies on the assumption that the vessel sails at constant speed and does not change its direction. Also, in the present form it does not account for the possible widening of the wake wedge for higher subcritical depth Froude numbers. Refinements of the method to include multiple observation points may be able to resolve finer details of the ship motion.
The most important value of the spectrogram analysis of one-point wave measurements presented in this paper is its ability to extract the key parameters of even overlapping in space or time wake components and in this way to generate a substantially better understanding of the characteristics and potential impact of the wakes. The method allows both the analysis of individual wake components and the comparison of wake structures produced by different vessels. Spectrograms can also be used to indicate whether or not the wake follows the classical Kelvin wake theory. In this case the ship should be moving in deep water and the length Froude number should be known. It would then be possible to see if wake measurements conform to the analytical solution presented here (figure 4). We do not address this question here, since our length Froude numbers are relatively small (
![]() ${\sim}0.3$
).
${\sim}0.3$
).
The spectrogram representation is particularly useful for decomposing the wake signal into distinct wave components, and for estimating the energy content of each of these components. Until recently, although many medium- and high-energy shorelines have been affected by vessel wakes for many years, the effects have either been negligible or accepted as reasonable (Kurennoy et al. Reference Kurennoy, Parnell and Soomere2011). However, following the introduction of a new generation of strongly powered ships, new and significant adverse effects have been observed in numerous locations (Parnell & Kofoed-Hansen Reference Parnell and Kofoed-Hansen2001; Soomere Reference Soomere2007). The actual effect of wakes of such ships obviously depends upon the features of the coastal environment and the existing hydrodynamic loads. It has become customary to associate the strongest loads on the coastal environment with specific high, long, long-crested and apparently nonlinear waves (Soomere Reference Soomere2007). The representation used in this paper makes it possible for the first time to adequately quantify this mostly qualitative conjecture in terms of not only the height or direction of waves but also of the duration and spectral structure. This opens a way to upgrade the existing ‘blanket regulations’ (that mostly rely on the primary properties such as wave height or period) towards much more detailed comparison of the acceptable and tolerated level of hydrodynamic loads in medium-energy environments. In particular, this approach has clear potential to adequately account for the significant variability in the data records for the same vessel at different times at the same location, and at different locations (Parnell & Kofoed-Hansen Reference Parnell and Kofoed-Hansen2001). As a result, future regulations related to ship wake impact may therefore be targeted more specifically to limitation of individual wake components, as the structural properties of wakes (and thus the largest hydrodynamic loads) seem to be quite stable.
To our knowledge, the results as shown in table 3 represent the first attempt to identify the energy of various wake components based on their separation in time–frequency space. In essence, this information may be very useful for ship design as it allows in a certain sense tracking of the properties of waves produced by different sections of the hull back to their origin. It is of clear value to better understand the impact of ship wakes at different depths and in the coastal zone (e.g. Parnell & Kofoed-Hansen Reference Parnell and Kofoed-Hansen2001; Soomere Reference Soomere2007; Soomere, Parnell & Didenkulova Reference Soomere, Parnell and Didenkulova2009; Soomere et al. Reference Soomere, Parnell and Didenkulova2011). For example, it was demonstrated that ship wakes at Aegna lead to intense beach erosion. In contrast, Pikakari Beach is in equilibrium with respect to both ship and wind waves, which could be attributed to its specific convex shape. At the Aegna measurement site, ship-wake impact is relatively short but intense. The energy in the precursor wave system is relatively small, but these waves may play an important role in resuspending sediment in deep water at this site. In comparison, at Pikakari Beach the wave energy is more evenly distributed between the cusp wave system and the following divergent and transverse wave systems. Given the intensity of ship traffic (figure 5), this implies that ship wakes are a much more persistent component in the general wave spectrum than has previously been recognized. This feature may also be a clue to understanding of the formation of the special convex beach profile at Pikakari (Didenkulova & Soomere Reference Didenkulova and Soomere2011).
Finally we underline that, while clearly useful, the method does not resolve intrinsic limitations associated with the wake detection and analysis. As is the case with any other method, it relies on the investigator’s discerning judgment to define what constitutes an event (in this case, a single wake). As is the case with any physical process, the details of the phenomenon can be affected by specific features of the site (e.g. figure 8), so a good understanding of the fundamentals of the process is necessary. Automating wake detection can be difficult in regions with high frequency of ship traffic, where wake features often are overlapping.
Acknowledgements
This work was supported by the European Union through support to the Estonian Centre of Excellence for Non-linear Studies (CENS) from the European Regional Development Fund, and targeted financing by the Estonian Ministry of Education and Research (grants SF0140007s11 and IUT33-3). The work was also supported by the grant MK-1146.2014.5, the Estonian Science Foundation (from 2011 Estonian Research Council) grants MTT63, ETF-8870 and ETF-9125, and by Russian State Contract Number 2014/133.