Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aseyev, Aleksandr S.
and
Cal, Raúl Bayoán
2016.
Vortex identification in the wake of amodelwind turbine array.
Journal of Turbulence,
Vol. 17,
Issue. 4,
p.
357.
F., Enrile
G., Besio
and
A., Stocchino
2018.
Shear and shearless Lagrangian structures in compound channels.
Advances in Water Resources,
Vol. 113,
Issue. ,
p.
141.
David, M. Jimreeves
Mathur, Manikandan
Govardhan, R. N.
and
Arakeri, J. H.
2018.
The kinematic genesis of vortex formation due to finite rotation of a plate in still fluid.
Journal of Fluid Mechanics,
Vol. 839,
Issue. ,
p.
489.
Melius, Matthew S.
Mulleners, Karen
and
Cal, Raúl Bayoán
2019.
Coherent Structure Interaction During Unsteady Separation.
AIAA Journal,
Vol. 57,
Issue. 8,
p.
3239.
Reijtenbagh, Jesse
Westerweel, Jerry
and
van de Water, Willem
2021.
Large-scale structures of scalar and velocity in a turbulent jet flow.
Physical Review Fluids,
Vol. 6,
Issue. 8,
Eisma, Jerke
Westerweel, Jerry
and
van de Water, Willem
2021.
Do coherent structures organize scalar mixing in a turbulent boundary layer?.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Cui, Zhiwen
and
Zhao, Lihao
2021.
A method for long-time integration of Lyapunov exponent and vectors along fluid particle trajectories.
Physics of Fluids,
Vol. 33,
Issue. 12,
Saltar, German
Lagares, Christian J.
and
Araya, Guillermo
2022.
Compressibility and Reynolds number effect on Lagrangian Coherent Structures (LCS).
Wang, Yu-Shuai
Wu, Bin
Gao, Chao
Yuan, Xian-Shi
Zhang, Yi-Xing
Wang, Na
Xu, Ze-Yang
Li, Yue-Qiang
Wang, Yu-Ling
and
Hao, Dong-Dong
2022.
Lagrangian analysis of the flow induced by a dielectric barrier discharge plasma actuator array under burst mode actuation.
AIP Advances,
Vol. 12,
Issue. 11,
Aksamit, Nikolas O.
and
Haller, George
2022.
Objective momentum barriers in wall turbulence.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Rist, Ulrich
Weinschenk, Matthias
and
Wenzel, Christoph
2023.
Investigation of Lagrangian Areas of Minimal Stretching (LAMS) in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 970,
Issue. ,
Santhosh, Sreejith
Qin, Haodong
Klose, Bjoern F.
Jacobs, Gustaaf B.
Vétel, Jérôme
and
Serra, Mattia
2023.
Spike formation theory in three-dimensional flow separation.
Journal of Fluid Mechanics,
Vol. 969,
Issue. ,
Lagares, Christian
and
Araya, Guillermo
2024.
Aquila-LCS: GPU/CPU-accelerated particle advection schemes for large-scale simulations.
SoftwareX,
Vol. 27,
Issue. ,
p.
101836.
Hayat, Imran
Black, Ryan T.
and
Park, George Ilhwan
2024.
Reference map technique for Lagrangian exploration of coherent structures.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
Aksamit, Nikolas
Katurji, Marwan
and
Zhang, Jiawei
2024.
Understanding Coherent Turbulence and the Roll‐Cell Transition With Lagrangian Coherent Structures and Frame‐Indifferent Fluxes.
Journal of Geophysical Research: Atmospheres,
Vol. 129,
Issue. 18,
Zhu, Dongpo
Zhao, Lei
Feng, Xiaoming
and
Tian, Guizhong
2024.
Experimental study of turbulent drag reduction characteristics of biomimetic divergent spines surfaces based on particle image velocimetry and proper orthogonal decomposition.
Ocean Engineering,
Vol. 311,
Issue. ,
p.
119007.
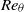 ${\mathit{Re}}_{\theta } $ of 9800 are identified in a plane parallel to the wall at
${\mathit{Re}}_{\theta } $ of 9800 are identified in a plane parallel to the wall at 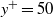 ${y}^{+ } = 50$. Three-component high-speed stereo particle image velocimetry measurements on a two-dimensional rectangular plane are used for the analysis. The velocity field is extended in the streamwise direction, using Taylor’s frozen field hypothesis. A computational approach utilizing the variational theory of hyperbolic Lagrangian coherent structures is applied to the domain and trajectories are computed using the extended field. The method identified both attracting and repelling Lagrangian coherent structures. There are no apparent differences in distribution of size, orientation and location of attracting and repelling structures. Hyperbolic behaviour appeared in the fluid at and around points of intersection between the attracting and repelling Lagrangian coherent structures. The network of curves identifying distinct regions of coherent flow patterns is displayed in observed relationship between the arrangement of Lagrangian coherent structures and various Eulerian fields.
${y}^{+ } = 50$. Three-component high-speed stereo particle image velocimetry measurements on a two-dimensional rectangular plane are used for the analysis. The velocity field is extended in the streamwise direction, using Taylor’s frozen field hypothesis. A computational approach utilizing the variational theory of hyperbolic Lagrangian coherent structures is applied to the domain and trajectories are computed using the extended field. The method identified both attracting and repelling Lagrangian coherent structures. There are no apparent differences in distribution of size, orientation and location of attracting and repelling structures. Hyperbolic behaviour appeared in the fluid at and around points of intersection between the attracting and repelling Lagrangian coherent structures. The network of curves identifying distinct regions of coherent flow patterns is displayed in observed relationship between the arrangement of Lagrangian coherent structures and various Eulerian fields.