Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T13:18:50.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydrodynamics of a droplet passing through a microfluidic T-junction

Published online by Cambridge University Press:  27 April 2017

Yongping Chen Open the ORCID record for Yongping Chen [Opens in a new window]  and
Zilong Deng
Yongping Chen*
Affiliation:
Jiangsu Key Laboratory of Micro and Nano Heat Fluid Flow Technology and Energy Application, School of Environmental Science and Engineering, Suzhou University of Science and Technology, Suzhou 215009, PR China Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, School of Energy and Environment, Southeast University, Nanjing 210096, PR China
Zilong Deng
Affiliation:
Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, School of Energy and Environment, Southeast University, Nanjing 210096, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a phase-field multiphase lattice Boltzmann model to systematically investigate the dynamic behaviour of a droplet passing through a microfluidic T-junction, especially focusing on the non-breakup of the droplet. Detailed information on the breakup and non-breakup is presented, together with the quantitative evolutions of driving and resistance forces as well as the droplet deformation characteristics involved. Through comparisons between cases of non-breakup and breakup, we find that the appearance of tunnels (the lubricating film between droplet and channel walls) provides a precondition for the final non-breakup of droplets, which slows down the droplet deformation rate and even induces non-breakup. The vortex flow formed inside droplets plays an important role in determining whether they break up or not. In particular, when the strength of vortex flow exceeds a critical value, a droplet can no longer break up. Additionally, more effort has been devoted to investigating the effects of viscosity ratio between disperse and continuous phases and width ratio between branch and main channels on droplet dynamic behaviours. It is found that a large droplet viscosity results in a small velocity gradient in a droplet, which restricts vortex generation and thus produces lower deformation resistance. Consequently, it is easier to break up a droplet with larger viscosity. Our work also reveals that a droplet in small branch channels tends to obstruct the channels and have small vortex flows, which induces easier breakup too. 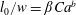Eventually, several phase diagrams for droplet flow patterns are provided, and the corresponding power-law correlations ($l_{0}/w=\unicode[STIX]{x1D6FD}Ca^{b}$, where 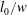$l_{0}/w$ is dimensionless initial droplet length and 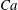$Ca$ is capillary number) are fitted to describe the boundaries between different flow patterns.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops Micro-/Nano-fluid dynamics: Microfluidics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 819 , 25 May 2017 , pp. 401 - 434
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abate, A. R. & Weitz, D. A. 2011 Faster multiple emulsification with drop splitting. Lab on a Chip 11, 1911–1915.CrossRefGoogle Scholar
Adamson, D. N., Mustafi, D., Zhang, J. X. J., Zheng, B. & Ismagilov, R. F. 2006 Production of arrays of chemically distinct nanolitre plugs via repeated splitting in microfluidic devices. Lab on a Chip 6 (9), 1178–1186.CrossRefGoogle ScholarPubMed
Afkhami, S., Leshansky, A. M. & Renardy, Y. 2011 Numerical investigation of elongated drops in a microfluidic T-junction. Phys. Fluids 23 (2), 022002.CrossRefGoogle Scholar
Baroud, C. N., Gallaire, F. & Dangla, R. 2010 Dynamics of microfluidic droplets. Lab on a Chip 10 (16), 2032–2045.CrossRefGoogle ScholarPubMed
Cahn, J. W. & Hilliard, J. E. 1958 Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (2), 258–267.CrossRefGoogle Scholar
Chai, Z. H. & Zhao, T. S. 2012 Effect of the forcing term in the multiple-relaxation-time lattice Boltzmann equation on the shear stress or the strain rate tensor. Phys. Rev. E 86 (1), 016705.Google ScholarPubMed
Christopher, G. F., Bergstein, J., End, N. B., Poon, M., Nguyen, C. & Anna, S. L. 2009 Coalescence and splitting of confined droplets at microfluidic junctions. Lab on a Chip 9 (8), 1102–1109.CrossRefGoogle ScholarPubMed
Connington, K. W., Miskin, M. Z., Lee, T., Jaeger, H. M. & Morris, J. F. 2015 Lattice Boltzmann simulations of particle-laden liquid bridges: effects of volume fraction and wettability. Intl J. Multiphase Flow 76, 32–46.CrossRefGoogle Scholar
De Menech, M. 2006 Modeling of droplet breakup in a microfluidic T-shaped junction with a phase-field model. Phys. Rev. E 73, 031505.Google Scholar
De Menech, M., Garstecki, P., Jousse, F. & Stone, H. A. 2008 Transition from squeezing to dripping in a microfluidic T-shaped junction. J. Fluid Mech. 595, 141–161.CrossRefGoogle Scholar
Farokhirad, S., Morris, J. F. & Lee, T. H. 2015 Coalescence-induced jumping of droplet: inertia and viscosity effects. Phys. Fluids 27 (10), 102102.CrossRefGoogle Scholar
Fu, T. & Ma, Y. 2015 Bubble formation and breakup dynamics in microfluidic devices: a review. Chem. Engng Sci. 135, 343–372.CrossRefGoogle Scholar
Fu, T., Ma, Y., Funfschilling, D. & Li, H. Z. 2011 Dynamics of bubble breakup in a microfluidic T-junction divergence. Chem. Engng Sci. 66, 4184–4195.CrossRefGoogle Scholar
van der Graaf, S., Nisisako, T., Schroen, C., van der Sman, R. G. M. & Boom, R. M. 2006 Lattice Boltzmann simulations of droplet formation in a T-shaped microchannel. Langmuir 22 (9), 4144–4152.CrossRefGoogle Scholar
Gunstensen, A. K., Rothman, D. H., Zaleski, S. & Zanetti, G. 1991 Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 43 (8), 4320–4327.CrossRefGoogle ScholarPubMed
Hoang, D. A.2013 Breakup of confined droplets in microfluidics. PhD thesis, Delft University of Technology.Google Scholar
Hoang, D. A., Portela, L. M., Kleijn, C. R., Kreutzer, M. T. & van Steijn, V. 2013 Dynamics of droplet breakup in a T-junction. J. Fluid Mech. 717, R4.CrossRefGoogle Scholar
Jacqmin, D. 1999 Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 155 (1), 96–127.CrossRefGoogle Scholar
Jullien, M. C., Tsang Mui Ching, M. J., Cohen, C., Menetrier, L. & Tabeling, P. 2009 Droplet breakup in microfluidic T-junctions at small capillary numbers. Phys. Fluids 21, 072001.CrossRefGoogle Scholar
Kendon, V. M., Cates, M. E., Pagonabarraga, I., Desplat, J. C. & Bladon, P. 2001 Inertial effects in three-dimensional spinodal decomposition of a symmetric binary fluid mixture: a lattice Boltzmann study. J. Fluid Mech. 440, 147–203.CrossRefGoogle Scholar
Ladd, A. J. C. 1994 Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.CrossRefGoogle Scholar
Leshansky, A. M., Afkhami, S., Jullien, M. C. & Tabeling, P. 2012 Obstructed breakup of slender drops in a microfluidic T junction. Phys. Rev. Lett. 108 (26), 264502.CrossRefGoogle Scholar
Leshansky, A. M. & Pismen, L. M. 2009 Breakup of drops in a microfluidic T junction. Phys. Fluids 21, 023303.CrossRefGoogle Scholar
Li, Q., Luo, K. H., Kang, Q. J., He, Y. L., Chen, Q. & Liu, Q. 2016 Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 52, 62–105.CrossRefGoogle Scholar
Liang, H., Shi, B. C. & Chai, Z. H. 2016 Lattice Boltzmann modeling of three-phase incompressible flows. Phys. Rev. E 93 (1), 013308.Google ScholarPubMed
Liang, H., Shi, B. C., Guo, Z. L. & Chai, Z. H. 2014 Phase-field-based multiple-relaxation-time lattice Boltzmann model for incompressible multiphase flows. Phys. Rev. E 89 (5), 053320.Google ScholarPubMed
Link, D. R., Anna, S. L., Weitz, D. A. & Stone, H. A. 2004 Geometrically mediated breakup of drops in microfluidic devices. Phys. Rev. Lett. 92, 054503.CrossRefGoogle ScholarPubMed
Liu, H.2010 Modeling and simulation of droplet dynamics in microfluidic devices. PhD thesis, University of Strathclyde.Google Scholar
Liu, H. & Zhang, Y. 2009 Droplet formation in a T-shaped microfluidic junction. J. Appl. Phys. 106, 034906.Google Scholar
Liu, H. & Zhang, Y. 2011 Lattice Boltzmann simulation of droplet generation in a microfluidic cross-junction. Commun. Comput. Phys. 9 (5), 1235–1256.CrossRefGoogle Scholar
Liu, H., Zhang, Y. & Valocchi, A. J. 2012 Modeling and simulation of thermocapillary flows using lattice Boltzmann method. J. Comput. Phys. 231 (12), 4433–4453.CrossRefGoogle Scholar
Lou, Q., Guo, Z. & Shi, B. 2013 Evaluation of outflow boundary conditions for two-phase lattice Boltzmann equation. Phys. Rev. E 87 (6), 063301.Google ScholarPubMed
Lu, Y., Fu, T., Zhu, C., Ma, Y. & Li, H. Z. 2016 Dynamics of bubble breakup at a T junction. Phys. Rev. E 93, 022802.Google ScholarPubMed
Manga, M. 1996 Dynamics of drops in branched tubes. J. Fluid Mech. 315, 105–117.CrossRefGoogle Scholar
Rallison, J. M. 1984 The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid Mech. 16, 45–66.CrossRefGoogle Scholar
Roths, T., Friedrich, C., Marth, M. & Honerkamp, J. 2002 Dynamics and rheology of the morphology of immiscible polymer blends – on modeling and simulation. Rheol. Acta 41 (3), 211–222.CrossRefGoogle Scholar
Shan, X. & Chen, H. 1993 Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 47 (3), 1815–1819.Google ScholarPubMed
Shan, X. & Chen, H. 1994 Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation. Phys. Rev. E 49 (4), 2941–2948.Google ScholarPubMed
Shang, L. R., Cheng, Y., Wang, J., Yu, Y. R., Zhao, Y. J., Chen, Y. P. & Gu, Z. Z. 2016 Osmotic pressure-triggered cavitation in microcapsules. Lab on a Chip 16 (2), 251–255.CrossRefGoogle ScholarPubMed
Shi, Y., Tang, G. H. & Xia, H. H. 2014 Lattice Boltzmann simulation of droplet formation in T-junction and flow focusing devices. Comput. Fluids 90, 155–163.CrossRefGoogle Scholar
van der Sman, R. G. M. 2006 Galilean invariant lattice Boltzmann scheme for natural convection on square and rectangular lattices. Phys. Rev. E 74 (2), 026705.Google ScholarPubMed
Song, H., Tice, J. D. & Ismagilov, R. F. 2003 A microfluidic system for controlling reaction networks in time. Angew. Chem. Intl Ed. Engl. 42 (7), 768–772.CrossRefGoogle ScholarPubMed
Stone, H. A., Bentley, B. J. & Leal, L. G. 1986 An experimental-study of transient effects in the breakup of viscous drops. J. Fluid Mech. 173, 131–158.CrossRefGoogle Scholar
Swift, M. R., Orlandini, E., Osborn, W. R. & Yeomans, J. M. 1996 Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Phys. Rev. E 54 (5), 5041–5052.Google ScholarPubMed
Swift, M. R., Osborn, W. R. & Yeomans, J. M. 1995 Lattice Boltzmann simulation of nonideal fluids. Phys. Rev. Lett. 75 (5), 830–833.CrossRefGoogle ScholarPubMed
Thorsen, T., Roberts, R. W., Arnold, F. H. & Quake, S. R. 2001 Dynamic pattern formation in a vesicle-generating microfluidic device. Phys. Rev. Lett. 86 (18), 4163–4166.CrossRefGoogle Scholar
Vladisavljević, G. T., Khalid, N., Neves, M. A., Kuroiwa, T., Nakajima, M., Uemura, K., Ichikawa, S. & Kobayashi, I. 2013 Industrial lab-on-a-chip: design, applications and scale-up for drug discovery and delivery. Adv. Drug Deliv. Rev. 65 (11–12), 1626–1663.CrossRefGoogle ScholarPubMed
Wang, X., Zhu, C., Wu, Y., Fu, T. & Ma, Y. 2015 Dynamics of bubble breakup with partly obstruction in a microfluidic T-junction. Chem. Engng Sci. 132, 128–138.CrossRefGoogle Scholar
Zhao, Y. J., Zhao, X. W., Hu, J., Xu, M., Zhao, W. J., Sun, L. G., Zhu, C., Xu, H. & Gu, Z. Z. 2009 Encoded porous beads for label-free multiplex detection of tumor markers. Adv. Mater. 21 (5), 569–572.CrossRefGoogle ScholarPubMed
Zheng, B. & Ismagilov, R. F. 2005 A microfluidic approach for screening submicroliter volumes against multiple reagents by using preformed arrays of nanoliter plugs in a three-phase liquid/liquid/gas flow. Angew. Chem. Intl Ed. Engl. 44 (17), 2520–2523.CrossRefGoogle Scholar
Zhou, H. & Pozrikidis, C. 1993 The flow of suspensions in channels: single files of drops. Phys. Fluids A 5 (2), 311–324.CrossRefGoogle Scholar