Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T08:37:55.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydrodynamic diffusion of sedimenting point particles in a vertical shear flow

Published online by Cambridge University Press:  07 August 2013

Andrew Crosby  and
John R. Lister
Andrew Crosby*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
John R. Lister
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The hydrodynamic diffusion of sedimenting point particles in a vertically sheared periodic system is investigated numerically and theoretically. In both the velocity-gradient direction and the vorticity direction, the rate of hydrodynamic diffusion is reduced as the shear rate is increased. In the velocity-gradient direction, two-particle interactions cause no net displacement, and three-particle interactions are necessary for diffusive behaviour. In contrast to an unsheared system, the resulting diffusion coefficient is only weakly dependent upon the size of the system and 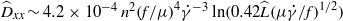${\widehat{D}}_{xx} \sim 4. 2\times 1{0}^{- 4} \hspace{0.167em} {n}^{2} {(f/ \mu )}^{4} {\dot {\gamma } }^{- 3} \ln (0. 42\widehat{L}{(\mu \dot {\gamma } / f)}^{1/ 2} )$, where $n$ is the particle number density, 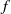$f$ the force per particle, 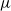$\mu $ the fluid viscosity, 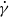$\dot {\gamma } $ the imposed shear rate, and 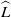$\widehat{L}$ the system size. In the vorticity direction, although individual two-particle interactions cause no net displacement, a superposition of interactions is sufficient to cause diffusion-like linear growth of the ensemble-averaged square particle displacements. The associated diffusion coefficient is given by 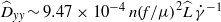${\widehat{D}}_{yy} \sim 9. 47\times 1{0}^{- 4} \hspace{0.167em} n{(f/ \mu )}^{2} \widehat{L}\hspace{0.167em} {\dot {\gamma } }^{- 1} $. At sufficiently long times, the effect of multi-particle interactions cannot be neglected and there is a transition to another regime in which the diffusion coefficient is similar in form, but slightly reduced from this value. The dependence of ${\widehat{D}}_{xx} $ and ${\widehat{D}}_{yy} $ on the number density and dimensionless shear rate is explained using theoretical scaling arguments and analyses.

JFM classification

Complex Fluids: Suspensions Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 699 - 732
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A., Batchelor, G. K., Hinch, E. J., Koch, D. L. & Mauri, R. 1992 Longitudinal shear-induced diffusion of spheres in a dilute suspension. J. Fluid Mech. 240, 651–657.CrossRefGoogle Scholar
Batchelor, G. K. 1972 Sedimentation in a dilute dispersion of spheres. J. Fluid Mech. 52 (2), 245–268.CrossRefGoogle Scholar
Boycott, A. E. 1920 Sedimentation of blood corpuscles. Nature 104 (2621), 532.CrossRefGoogle Scholar
Caflisch, R. E. & Luke, J. H. C. 1985 Variance in the sedimentation speed of a suspension. Phys. Fluids 28 (3), 759–760.CrossRefGoogle Scholar
Crosby, A. & Lister, J. R. 2012 Falling plumes of point particles in viscous fluid. Phys. Fluids 24 (12), 123101.CrossRefGoogle Scholar
Cunha, F. R., Abade, G. C., Sousa, A. J. & Hinch, E. J. 2002 Modeling and direct simulation of velocity fluctuations and particle-velocity correlations in sedimentation. Trans. ASME: J. Fluids Engng 124 (4), 957–968.Google Scholar
Davis, R. H. & Hassen, M. A. 1988 Spreading of the interface at the top of a slightly polydisperse sedimenting suspension. J. Fluid Mech. 196, 107–134.CrossRefGoogle Scholar
Eckstein, E. C., Bailey, D. G. & Shapiro, A. H. 1977 Self-diffusion of particles in shear flow of a suspension. J. Fluid Mech. 79 (1), 191–208.CrossRefGoogle Scholar
Ekiel-Jeżewska, M. L., Metzger, B. & Guazzelli, E. 2006 Spherical cloud of point particles falling in a viscous fluid. Phys. Fluids 18 (3), 038104.CrossRefGoogle Scholar
Guazzelli, E. & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–116.CrossRefGoogle Scholar
Ham, J. M. & Homsy, G. M. 1988 Hindered settling and hydrodynamic dispersion in quiescent sedimenting suspensions. Intl J. Multiphase Flow 14 (5), 533–546.CrossRefGoogle Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5 (2), 317–328.CrossRefGoogle Scholar
Ishii, K. 1979 Viscous flow past multiple planar arrays of small spheres. J. Phys. Soc. Japan 46 (2), 675–680.CrossRefGoogle Scholar
Kerr, R. C., Lister, J. R. & Mériaux, C. 2008 Effect of thermal diffusion on the stability of strongly tilted mantle plume tails. J. Geophys. Res. 113, B09401.Google Scholar
Koch, D. L. 1994 Hydrodynamic diffusion in a suspension of sedimenting point particles with periodic boundary conditions. Phys. Fluids 6 (9), 2894–2900.CrossRefGoogle Scholar
Koch, D. L. & Shaqfeh, E. S. G. 1991 Screening in sedimenting suspensions. J. Fluid Mech. 224, 275–303.CrossRefGoogle Scholar
Ladd, A. J. C. 1993 Dynamical simulations of sedimenting spheres. Phys. Fluids A 5 (2), 299–310.CrossRefGoogle Scholar
Lister, J. R., Kerr, R. C., Russell, N. J. & Crosby, A. 2011 Rayleigh–Taylor instability of an inclined buoyant viscous cylinder. J. Fluid Mech. 671, 313–338.CrossRefGoogle Scholar
Machu, G., Meile, W., Nitsche, L. C. & Schaflinger, U. 2001 Coalescence, torus formation and breakup of sedimenting drops: experiments and computer simulations. J. Fluid Mech. 447, 299–336.CrossRefGoogle Scholar
Metzger, B., Nicolas, M. & Guazzelli, E. 2007 Falling clouds of particles in viscous fluids. J. Fluid Mech. 580, 283–301.CrossRefGoogle Scholar
Mucha, P. J. & Brenner, M. P. 2003 Diffusivities and front propagation in sedimentation. Phys. Fluids 15 (5), 1305–1313.CrossRefGoogle Scholar
Nicolai, H. & Guazzelli, E. 1995 Effect of the vessel size on the hydrodynamic diffusion of sedimenting spheres. Phys. Fluids 7 (1), 3–5.CrossRefGoogle Scholar
Nicolai, H., Herzhaft, B., Hinch, E. J., Oger, L. & Guazzelli, E. 1995 Particle velocity fluctuations and hydrodynamic self-diffusion of sedimenting non-Brownian spheres. Phys. Fluids 7, 12–23.CrossRefGoogle Scholar
Nitsche, J. M. & Batchelor, G. K. 1997 Break-up of a falling drop containing dispersed particles. J. Fluid Mech. 340, 161–175.CrossRefGoogle Scholar
Pignatel, F., Nicolas, M., Guazzelli, E. & Saintillan, D. 2009 Falling jets of particles in viscous fluids. Phys. Fluids 21 (12), 123303.CrossRefGoogle Scholar
Saintillan, D., Darve, E. & Shaqfeh, E. S. G. 2005 A smooth particle-mesh Ewald algorithm for Stokes suspension simulations: the sedimentation of fibres. Phys. Fluids 17 (3), 033301.CrossRefGoogle Scholar
Sierou, A. & Brady, J. F. 2004 Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid Mech. 506, 285–314.CrossRefGoogle Scholar
Smoluchowski, M. S. 1913 On the practical applicability of Stokes’ law of resistance, and the modifications of it required in certain cases. In Proceedings of the Fifth International Congress of Mathematicians, vol. II. pp. 192–201. Cambridge University Press.Google Scholar