Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T09:17:50.620Z Has data issue: false hasContentIssue false
  • English
  • Français

How surface roughness reduces heat transport for small roughness heights in turbulent Rayleigh–Bénard convection

Published online by Cambridge University Press:  11 December 2017

Yi-Zhao Zhang ,
Chao Sun ,
Yun Bao  and
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window]
Yi-Zhao Zhang
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
Chao Sun
Affiliation:
Center for Combustion Energy and Department of Thermal Engineering, Tsinghua University, 100084 Beijing, China
Yun Bao
Affiliation:
Department of Mechanics, Sun Yat-Sen University, Guangzhou 510275, China
Quan Zhou*
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Rough surfaces have been widely used as an efficient way to enhance the heat-transfer efficiency in turbulent thermal convection. In this paper, however, we show that roughness does not always mean a heat-transfer enhancement, but in some cases it can also reduce the overall heat transport through the system. To reveal this, we carry out numerical investigations of turbulent Rayleigh–Bénard convection over rough conducting plates. 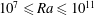Our study includes two-dimensional (2D) simulations over the Rayleigh number range $10^{7}\leqslant Ra\leqslant 10^{11}$ and three-dimensional (3D) simulations at 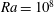$Ra=10^{8}$. The Prandtl number is fixed to 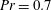$Pr=0.7$ for both the 2D and the 3D cases. At a fixed Rayleigh number $Ra$, reduction of the Nusselt number 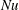$Nu$ is observed for small roughness height 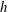$h$, whereas heat-transport enhancement occurs for large 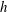$h$. The crossover between the two regimes yields a critical roughness height 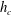$h_{c}$, which is found to decrease with increasing 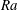$Ra$ as 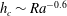$h_{c}\sim Ra^{-0.6}$. Through dimensional analysis, we provide a physical explanation for this dependence. The physical reason for the 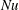$Nu$ reduction is that the hot/cold fluid is trapped and accumulated inside the cavity regions between the rough elements, leading to a much thicker thermal boundary layer and thus impeding the overall heat flux through the system.

JFM classification

Convection: Convection Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent Flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 836 , 10 February 2018 , R2
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Bao, Y., Chen, J., Liu, B.-F., She, Z.-S., Zhang, J. & Zhou, Q. 2015 Enhanced heat transport in partitioned thermal convection. J. Fluid Mech. 784, R5.Google Scholar
Biferale, L., Perlekar, P., Sbragaglia, M. & Toschi, F. 2012 Convection in multiphase fluid flows using lattice Boltzmann methods. Phys. Rev. Lett. 108, 104502.CrossRefGoogle ScholarPubMed
Chen, J., Bao, Y., Yin, Z.-X. & She, Z.-S. 2017 Theoretical and numerical study of enhanced heat transfer in partitioned thermal convection. Intl J. Heat Mass Transfer 115, 556–569.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google ScholarPubMed
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.Google Scholar
Ciliberto, S. & Laroche, C. 1999 Random roughness of boundary increases the turbulent convection scaling exponent. Phys. Rev. Lett. 82, 3998–4001.CrossRefGoogle Scholar
Du, Y.-B. & Tong, P. 1998 Enhanced heat transport in turbulent convection over a rough surface. Phys. Rev. Lett. 81, 987–990.Google Scholar
Du, Y.-B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.CrossRefGoogle Scholar
Fadlun, E. A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary/finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 161, 35–60.CrossRefGoogle Scholar
Goluskin, D. & Doering, C. R. 2016 Bounds for convection between rough boundaries. J. Fluid Mech. 804, 370–376.Google Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement-induced heat transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.Google Scholar
Jiang, H.-C., Zhu, X.-J., Mathai, V., Verzicco, R., Lohse, D. & Sun, C. 2017 Controlling heat transport and flow structures in thermal turbulence using ratchet surfaces. Phys. Rev. Lett. (submitted).Google Scholar
Jin, X.-L. & Xia, K.-Q. 2008 An experimental study of kicked thermal turbulence. J. Fluid Mech. 606, 133–151.CrossRefGoogle Scholar
Lakkaraju, R., Stevens, R. J. A. M., Oresta, P., Verzicco, R., Lohse, D. & Prosperetti, A. 2013 Heat transport in bubbling turbulent Rayleigh–Bénard convection. Proc. Natl. Acad. Sci. USA 110, 9237–9242.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
van der Poel, E. P., Stevens, R. J. A. M. & Lohse, D. 2013 Comparison between two- and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 736, 177–194.Google Scholar
du Puits, R., Li, L., Resagk, C. & Thess, A. 2014 Turbulent boundary layer in high Rayleigh number convection in air. Phys. Rev. Lett. 112, 124301.Google Scholar
Qiu, X.-L., Xia, K.-Q. & Tong, P. 2005 Experimental study of velocity boundary layer near a rough conducting surface in turbulent natural convection. J. Turbul. 6, 30.Google Scholar
Roche, R.-E, Castaing, B., Chabaud, B. & Hebral, B. 2001 Observation of the 1/2 power law in Rayleigh–Bénard convection. Phys. Rev. E 63, 045303(R).Google Scholar
Salort, J., Liot, O., Rusaouen, E., Seychelles, F., Tisserand, J.-C., Creyssels, M., Castaing, B. & Chillà, F. 2014 Thermal boundary layer near roughnesses in turbulent Rayleigh–Bénard convection: flow structure and multistability. Phys. Fluids 26, 015112.CrossRefGoogle Scholar
Shen, Y., Tong, P. & Xia, K.-Q. 1996 Turbulent convection over rough surfaces. Phys. Rev. Lett. 76, 908–911.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Shishkina, O. & Wagner, C. 2011 Modelling the influence of wall roughness on heat transfer in thermal convection. J. Fluid Mech. 686, 568–582.CrossRefGoogle Scholar
Stringano, G., Pascazio, G. & Verzicco, R. 2006 Turbulent thermal convection over grooved plates. J. Fluid Mech. 557, 307–336.Google Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2009 Flow organization in two-dimensional non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. J. Fluid Mech. 637, 105–135.Google Scholar
Sun, C. & Zhou, Q. 2014 Experimental techniques for turbulent Taylor–Couette flow and Rayleigh–Bénard convection. Nonlinearity 27, R89–R121.CrossRefGoogle Scholar
Tisserand, J.-C., Creyssels, M., Gasteuil, Y., Pabiou, H., Gibert, M., Castaing, B. & Chillà, F. 2011 Comparison between rough and smooth plates within the same Rayleigh–Bénard cell. Phys. Fluids 23, 015105.Google Scholar
Toppaladoddi, S., Succi, S. & Wettlaufer, J. S. 2017 Roughness as a route to the ultimate regime of thermal convection. Phys. Rev. Lett. 118, 074503.Google Scholar
Villermaux, E. 1998 Transfer at rough sheared interfaces. Phys. Rev. Lett. 81, 4859–4862.Google Scholar
Wagner, S. & Shishkina, O. 2015 Heat flux enhancement by regular surface roughness in turbulent thermal convection. J. Fluid Mech. 763, 109–135.Google Scholar
Wei, P., Chan, T.-S., Ni, R., Zhao, X.-Z. & Xia, K.-Q. 2014 Heat transport properties of plates with smooth and rough surfaces in turbulent thermal convection. J. Fluid Mech. 740, 28–46.Google Scholar
Xie, Y.-C & Xia, K.-Q. 2017 Turbulent thermal convection over rough plates with varying roughness geometries. J. Fluid Mech. 825, 573–599.Google Scholar
Zhang, Y., Zhou, Q. & Sun, C. 2017 Statistics of kinetic and thermal energy dissipation rates in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 814, 165–184.Google Scholar
Zhong, J.-Q., Funfschilling, D. & Ahlers, G. 2009a Enhanced heat transport by turbulent two-phase Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 124501.Google Scholar
Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009b Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.Google ScholarPubMed
Zhou, Q. & Xia, K.-Q. 2010 Universality of local dissipation scales in buoyancy-driven turbulence. Phys. Rev. Lett. 104, 124301.Google Scholar
Zhou, Q. & Xia, K.-Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.CrossRefGoogle Scholar
Zhu, X., Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2016 Direct numerical simulation of Taylor–Couette flow with grooved walls: torque scaling and flow structure. J. Fluid Mech. 794, 746–774.Google Scholar
Zhu, X., Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2017 Roughness-facilitated local 1/2 scaling does not imply the onset of the ultimate regime of thermal convection. Phys. Rev. Lett. 119, 154501.CrossRefGoogle Scholar

Zhang et al. supplementary movie

The movie about the instantaneous temperature (color) and velocity (arrows) fields near the center of the bottom plate. The data are obtained in the smooth cell (upper left) and in the rough cells with triangular roughness elements (black lines) of height h/h_c = 0.28 (upper right), 0.71 (lower left), and 1.42 (lower right).

Download Zhang et al. supplementary movie(Video)
Video 13.5 MB