1. Introduction
Thin falling films flowing down vertical heated walls are efficient in evaporation processes due to the large surface area to volume ratio of the film. Therefore, vertical falling film evaporators can operate at small temperature differences and are frequently used in, for example, the food and pulp and paper industries to evaporate water from the liquid product (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023) or in desalination applications (Dai et al. Reference Dai, Zhang, Wang, Nawaz and Jacobi2022). In such evaporators, the liquid product typically flows inside or outside of a vertical steel tube that is heated on the other side by condensing steam (Schnabel Reference Schnabel2010). The evaporation takes place at the free surface of the product film and the heat transfer resistance is generally much higher in the liquid product than for the condensed steam film or the tube wall (Numrich Reference Numrich1995). Thus, the heat transfer resistance of the film should be minimised to design efficient evaporators. To achieve this, we need a thorough understanding of the heat transfer mechanisms between the wall and the film surface.
Usually, the heat exchange surface is smooth due to the relatively simple and cheap manufacturing process. The heat transfer in vertical falling films on smooth surfaces has been thoroughly studied before. Nusselt (Reference Nusselt1916) derived analytical solutions for the heat and mass transfer in smooth laminar falling films by disregarding the effects of interfacial waves and gas phase interactions. However, with increasing the flow rate, the flow transitions from a flat laminar film to a wavy one (characterised by the formation of solitary waves) and eventually becomes fully turbulent (Kapitza & Ter Haar Reference Kapitza and Ter Haar1948; Al-Sibai Reference Al-Sibai2006; Åkesjö et al. Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2017). The solitary wave should here be understood as a large-amplitude wave which propagates with a constant shape in the reference frame of the wave (Dietze, Leefken & Kneer Reference Dietze, Leefken and Kneer2008; Denner et al. Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016). The flow conditions govern the hydrodynamics that has been shown to significantly influence the heat transport in the film. Miyara (Reference Miyara1999), Serifi, Malamataris & Bontozoglou (Reference Serifi, Malamataris and Bontozoglou2004) and Kunugi & Kino (Reference Kunugi and Kino2005) studied numerically the effects of solitary waves on the heat transfer in falling films. The findings showed that the solitary waves enhanced the heat transfer rate through the film above the conduction limit due to film thinning between the waves and convection effects (mixing) in the waves. Åkesjö et al. (Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2018) studied experimentally and numerically the effect of the hydrodynamics on the film heat transfer for smooth vertical pipes in laminar-to-turbulent flow regimes. The results showed a strong influence of the film thickness and mixing caused by backflow in streamwise waves on the heat transfer. Additionally, the same authors found that the transition from two- to three-dimensional waves did not have a significant effect on the heat transfer. Kalliadasis et al. (Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012) showed, using two-dimensional reduced-order models, that the recirculation in solitary waves increases with their amplitude and induces mixing of the temperature field that enhances the heat transport. Markides, Mathie & Charogiannis (Reference Markides, Mathie and Charogiannis2016) investigated experimentally the heat transfer in film flowing down an inclined foil and observed heat transfer rates up to three times higher than those predicted by the Nusselt theory. The authors suggest that unsteady flow phenomena associated with the interface waves contribute to the enhancement.
To further improve the heat transfer rate through the film, previous studies have suggested introducing surface modifications on the heated wall (Webb & Kim Reference Webb and Kim2005). There are two potential benefits of such modifications on the total heat transfer rate ![]() $Q = hA(T_{wall}-T_{sat})$, where
$Q = hA(T_{wall}-T_{sat})$, where ![]() $T_{wall}$ and
$T_{wall}$ and ![]() $T_{sat}$ are the wall and saturation temperatures, respectively. First, the modifications can alter the hydrodynamics (see Aksel & Schörner (Reference Aksel and Schörner2018) for an extensive review of the hydrodynamic effects) to increase the heat transfer coefficient
$T_{sat}$ are the wall and saturation temperatures, respectively. First, the modifications can alter the hydrodynamics (see Aksel & Schörner (Reference Aksel and Schörner2018) for an extensive review of the hydrodynamic effects) to increase the heat transfer coefficient ![]() $h$. Secondly, the modifications can increase the heat transfer area
$h$. Secondly, the modifications can increase the heat transfer area ![]() $A$. Still, it is generally preferred to increase
$A$. Still, it is generally preferred to increase ![]() $h$ without significant change of
$h$ without significant change of ![]() $A$ since increasing
$A$ since increasing ![]() $A$ typically requires more material, increased manufacturing complexity and thus higher costs (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). Here, we therefore focus on modified surfaces that primarily increase
$A$ typically requires more material, increased manufacturing complexity and thus higher costs (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). Here, we therefore focus on modified surfaces that primarily increase ![]() $h$.
$h$.
Because of the wide range of applications with disparate practical considerations (such as heat-sensitive fluids, sputtering, fouling, residence times, etc.) there exist no general design guidelines for surface modifications in vertical falling film evaporators (Lozano Avilés Reference Lozano Avilés2007). However, previous works have shown a potential for improving the heat or scalar transfer rate by more than ![]() $100\,\%$ using various designs of surface modifications in a wide range of applications. Here, we disregard studies focusing on surface modifications that induce nucleate boiling since the temperature difference is typically too low to initiate boiling in heat-sensitive fluids, and the associated (micro)structures, and vapour bubbles, may increase the risk of fouling in the evaporator (Tuoc Reference Tuoc2015; Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). Surface modifications were observed to alter the film flow characteristics in, for example, Slade et al. (Reference Slade, Veremieiev, Lee and Gaskell2013) and Li et al. (Reference Li, Yi, Li, Pavlenko and Gao2018) and, in Yu et al. (Reference Yu, Loffler, Gambaryan-Roisman and Stephan2010), a grooved surface was shown to reduce the wall temperature during heating conditions. Najim et al. (Reference Najim, Feddaoui, Nait Alla and Charef2018) studied numerically a sinusoidal heat transfer surface and observed a heat transfer enhancement of up to 10 % depending on the amplitude and number of wall waves. Raach & Mitrovic (Reference Raach and Mitrovic2005) investigated numerically the effect of introducing turbulence wires in the film on the evaporation rate. The authors found that two wires in series (as opposed to a single wire) gave significant enhancement of turbulence and suggest an optimal spacing of 18 wire diameters between the wires. The study found a 100 % increase in evaporation rate but did not explain thoroughly the underlying mechanisms. Salvagnini & Taqueda (Reference Salvagnini and Taqueda2004) measured the evaporation rate of vertical falling film on a tube with a wire mesh. They observed enhancements of around 100 %–200 % depending on the film Reynolds number. Zheng & Worek (Reference Zheng and Worek1996) observed experimentally a heat transfer enhancement by adding rods in an inclined film. The authors suggested the enhancement is due to circulating zones generated by the rods and found that the optimal rod separation was 5 cm. Lozano Avilés (Reference Lozano Avilés2007) provided a detailed overview of studies using different types of structured surfaces and also investigated experimentally a vertically (longitudinal) grooved surface that enhanced the heat transfer by approximately 40 %. The latter study suggests that structures perpendicular to the flow are the most effective at disrupting the boundary layer and inducing mixing although such structures may induce stagnant liquid zones and are potentially problematic for liquids with solid particles. In this study, we focus on understanding the mechanisms that enhance the convective heat transfer and do not consider those potential issues in certain applications. For that purpose, we focus on perpendicular surface modifications that show the greatest potential for convective heat transfer enhancement.
$100\,\%$ using various designs of surface modifications in a wide range of applications. Here, we disregard studies focusing on surface modifications that induce nucleate boiling since the temperature difference is typically too low to initiate boiling in heat-sensitive fluids, and the associated (micro)structures, and vapour bubbles, may increase the risk of fouling in the evaporator (Tuoc Reference Tuoc2015; Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). Surface modifications were observed to alter the film flow characteristics in, for example, Slade et al. (Reference Slade, Veremieiev, Lee and Gaskell2013) and Li et al. (Reference Li, Yi, Li, Pavlenko and Gao2018) and, in Yu et al. (Reference Yu, Loffler, Gambaryan-Roisman and Stephan2010), a grooved surface was shown to reduce the wall temperature during heating conditions. Najim et al. (Reference Najim, Feddaoui, Nait Alla and Charef2018) studied numerically a sinusoidal heat transfer surface and observed a heat transfer enhancement of up to 10 % depending on the amplitude and number of wall waves. Raach & Mitrovic (Reference Raach and Mitrovic2005) investigated numerically the effect of introducing turbulence wires in the film on the evaporation rate. The authors found that two wires in series (as opposed to a single wire) gave significant enhancement of turbulence and suggest an optimal spacing of 18 wire diameters between the wires. The study found a 100 % increase in evaporation rate but did not explain thoroughly the underlying mechanisms. Salvagnini & Taqueda (Reference Salvagnini and Taqueda2004) measured the evaporation rate of vertical falling film on a tube with a wire mesh. They observed enhancements of around 100 %–200 % depending on the film Reynolds number. Zheng & Worek (Reference Zheng and Worek1996) observed experimentally a heat transfer enhancement by adding rods in an inclined film. The authors suggested the enhancement is due to circulating zones generated by the rods and found that the optimal rod separation was 5 cm. Lozano Avilés (Reference Lozano Avilés2007) provided a detailed overview of studies using different types of structured surfaces and also investigated experimentally a vertically (longitudinal) grooved surface that enhanced the heat transfer by approximately 40 %. The latter study suggests that structures perpendicular to the flow are the most effective at disrupting the boundary layer and inducing mixing although such structures may induce stagnant liquid zones and are potentially problematic for liquids with solid particles. In this study, we focus on understanding the mechanisms that enhance the convective heat transfer and do not consider those potential issues in certain applications. For that purpose, we focus on perpendicular surface modifications that show the greatest potential for convective heat transfer enhancement.
Heat transfer improvements of up to ![]() $100\,\%$ have also been observed in our previous experimental studies on a pilot-scale evaporator using perpendicular surface modifications under industrially relevant conditions (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). Although the results in the aforementioned studies with surface modifications are promising, it is not yet clear how and why the surface modifications enhance the heat transfer rate (Lozano Avilés Reference Lozano Avilés2007; Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023) and the underlying mechanisms for the heat transport in such cases have so far received relatively little attention (to the best of the authors’ knowledge). It is, therefore, important to understand the governing mechanisms behind the enhancement to facilitate optimal design of the modifications under various flow conditions and fluids. The present work thus aims at closing this knowledge gap by providing a general methodology and explanation of such mechanisms. For this purpose, we define a model problem consisting of a relatively simple representation of perpendicular surface modifications (see figure 1a), analogous to those used in Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023). These modifications have been shown to provide similar heat transfer enhancements as the other types of perpendicular structures used in the literature, and we thus believe that they are suitable for the purpose of this work. It should also be noted that although we choose here a specific model problem, the general formulation of the methodology developed in this work can be used to study the heat transfer mechanisms for any type of surface modifications.
$100\,\%$ have also been observed in our previous experimental studies on a pilot-scale evaporator using perpendicular surface modifications under industrially relevant conditions (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). Although the results in the aforementioned studies with surface modifications are promising, it is not yet clear how and why the surface modifications enhance the heat transfer rate (Lozano Avilés Reference Lozano Avilés2007; Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023) and the underlying mechanisms for the heat transport in such cases have so far received relatively little attention (to the best of the authors’ knowledge). It is, therefore, important to understand the governing mechanisms behind the enhancement to facilitate optimal design of the modifications under various flow conditions and fluids. The present work thus aims at closing this knowledge gap by providing a general methodology and explanation of such mechanisms. For this purpose, we define a model problem consisting of a relatively simple representation of perpendicular surface modifications (see figure 1a), analogous to those used in Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023). These modifications have been shown to provide similar heat transfer enhancements as the other types of perpendicular structures used in the literature, and we thus believe that they are suitable for the purpose of this work. It should also be noted that although we choose here a specific model problem, the general formulation of the methodology developed in this work can be used to study the heat transfer mechanisms for any type of surface modifications.

Figure 1. (a) Illustration of the surface modifications and the considered topological parameters pitch ![]() $\hat {p}$, height
$\hat {p}$, height ![]() $\hat {h}$ and length
$\hat {h}$ and length ![]() $\hat {l}$. (b) Schematic view of the problem. The liquid film flows along the modified wall in the gravitational direction
$\hat {l}$. (b) Schematic view of the problem. The liquid film flows along the modified wall in the gravitational direction ![]() $\boldsymbol {g}$. The wall temperature
$\boldsymbol {g}$. The wall temperature ![]() $T_{wall}$ is kept constant above the saturation temperature
$T_{wall}$ is kept constant above the saturation temperature ![]() $T_{sat}$ that is maintained at the gas–liquid interface and gas phase. The temperature difference induces a heat flux
$T_{sat}$ that is maintained at the gas–liquid interface and gas phase. The temperature difference induces a heat flux ![]() $q_{wall}$ from the wall towards the interface where the applied heat is absorbed by the heat flux
$q_{wall}$ from the wall towards the interface where the applied heat is absorbed by the heat flux ![]() $q_{evap}$ required for evaporation.
$q_{evap}$ required for evaporation.
At the industrial scale, evaporators may consist of a series of evaporator units, each comprising hundreds, or even thousands, of steel tubes, more than 10 m long. At such scales, it is also beneficial if the surface modifications are simple to manufacture, but yet effective, to be economically feasible. Bump-shaped corrugations, similar to our representation, were also found to improve interfacial scalar transfer in vertical falling films by more than 30 % (slightly more than the evaluated sinusoidal corrugations) in Dietze (Reference Dietze2019).
In this study, we aim to elucidate the heat transfer mechanisms behind the improved heat transport in the film, due to the surface modifications. To achieve this, we perform fully resolved direct numerical simulations (DNS) of evaporative falling films. We formulate in § 2.2 a heat flux decomposition that allows us to quantify and analyse the spatial distribution of mean and fluctuating advective and diffusive wall-normal heat fluxes through the film. The heat flux analyses are used to quantify and determine how the heat transfer is altered by the modifications. Based on the results, we propose a hypothesis of four synergistic mechanisms behind the heat transfer improvement in § 3.2. Additionally, we investigate the influence of flow conditions (§ 3.1), surface topology parameters (§§ 3.3.1 and 3.3.2) and material parameters (§ 3.3.3) on the heat fluxes and the overall heat transfer rate. Finally, we summarise our findings by analysing how key dimensionless parameters can explain and predict the overall heat transfer rate on both smooth and modified surfaces in § 3.4.
2. Methodology
We study the heat transfer in vertical falling films during evaporation conditions using multiphase DNS. Surface modifications are introduced at the wall to improve the heat transfer. The general design of the modifications is adopted from promising results in previous experimental studies at industrially relevant conditions (Sanches Romeiro Reference Sanches Romeiro2009; Åkesjö Reference Åkesjö2018; Åkesjö et al. Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2019, Reference Åkesjö, Gourdon, Jongsma and Sasic2023). These modifications are parameterised using the pitch ![]() $\hat {p}$ (vertical distance between modifications), height
$\hat {p}$ (vertical distance between modifications), height ![]() $\hat {h}$ (height of modification in wall-normal direction) and length
$\hat {h}$ (height of modification in wall-normal direction) and length ![]() $\hat {l}$ (length of modification in vertical direction). These parameters are non-dimensionalised using the viscous length scale
$\hat {l}$ (length of modification in vertical direction). These parameters are non-dimensionalised using the viscous length scale ![]() $(\nu _l^2/g)^{1/3}$ as further described in § 2.1. We avoid too-sharp edges on the modifications (that may cause numerical problems and excessive sputtering in real applications) by adopting a radius of
$(\nu _l^2/g)^{1/3}$ as further described in § 2.1. We avoid too-sharp edges on the modifications (that may cause numerical problems and excessive sputtering in real applications) by adopting a radius of ![]() $\hat {l}/2$ on the outer edges of the modifications. An illustration of the modifications is shown in figure 1(a).
$\hat {l}/2$ on the outer edges of the modifications. An illustration of the modifications is shown in figure 1(a).
In our analysis, we assume a constant wall temperature above saturation conditions ![]() $T_{wall}>T_{sat}$ on the product side. A constant wall temperature is reasonable if the wall Biot number satisfies
$T_{wall}>T_{sat}$ on the product side. A constant wall temperature is reasonable if the wall Biot number satisfies ![]() ${Bi} = ht_w/k_w \ll 1$ (where
${Bi} = ht_w/k_w \ll 1$ (where ![]() $h$ is the heat transfer coefficient on the product side of the wall,
$h$ is the heat transfer coefficient on the product side of the wall, ![]() $t_w$ is the wall thickness and
$t_w$ is the wall thickness and ![]() $k_w$ is the wall thermal conductivity) and the condensing steam maintains the steam side of the wall at the steam saturation temperature. The
$k_w$ is the wall thermal conductivity) and the condensing steam maintains the steam side of the wall at the steam saturation temperature. The ![]() ${Bi}\ll 1$ implies that the heat conduction in the wall dominates the heat transfer rate in the film, thus homogenising the wall temperature in the vertical direction. We further assume that the gas phase on the product side is pure vapour and that the gas–liquid interface (and the gas phase) is at saturation conditions (Schnabel Reference Schnabel2010; Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023).
${Bi}\ll 1$ implies that the heat conduction in the wall dominates the heat transfer rate in the film, thus homogenising the wall temperature in the vertical direction. We further assume that the gas phase on the product side is pure vapour and that the gas–liquid interface (and the gas phase) is at saturation conditions (Schnabel Reference Schnabel2010; Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023).
The evaporation rate is typically insignificant compared with the rate of the liquid product flow (p. 1290 in Schnabel (Reference Schnabel2010)). To justify this assumption, we consider a representative case of an evaporative falling film defined by ![]() $\mathit {Re}=100$ and
$\mathit {Re}=100$ and ![]() $\mathit {Nu}=0.5$ over a length of
$\mathit {Nu}=0.5$ over a length of ![]() $1000\delta _N$ Nusselt film thicknesses (these parameters are defined later). Taking liquid properties from the industrial fluid used in the experiments of Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023) and using the latent heat of water as 2320 kJ kg
$1000\delta _N$ Nusselt film thicknesses (these parameters are defined later). Taking liquid properties from the industrial fluid used in the experiments of Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023) and using the latent heat of water as 2320 kJ kg![]() $^{-1}$, we get a reduction of the liquid mass flow rate of
$^{-1}$, we get a reduction of the liquid mass flow rate of ![]() $4\,\%$ at the end of the section. For the cases considered in the present study, the film thickness is therefore practically constant. We assume the gas phase dynamics does not significantly influence the heat transfer in the liquid phase. This is partly due to the typical density
$4\,\%$ at the end of the section. For the cases considered in the present study, the film thickness is therefore practically constant. We assume the gas phase dynamics does not significantly influence the heat transfer in the liquid phase. This is partly due to the typical density ![]() $\rho _r = \rho _l / \rho _g = O(1000)$ and viscosity
$\rho _r = \rho _l / \rho _g = O(1000)$ and viscosity ![]() $\mu _r = \mu _l / \mu _g = O(100)$ ratios that indicate that relatively low pressure and viscous forces act on the interface by the gas at moderate relative velocities. As a rough estimate of when the gas phase velocity becomes significant, we consider a laminar vertical falling film with a no-slip wall and continuous shear stress at the gas–liquid interface. Here, the wall-normal shear stress distribution in the liquid is given by
$\mu _r = \mu _l / \mu _g = O(100)$ ratios that indicate that relatively low pressure and viscous forces act on the interface by the gas at moderate relative velocities. As a rough estimate of when the gas phase velocity becomes significant, we consider a laminar vertical falling film with a no-slip wall and continuous shear stress at the gas–liquid interface. Here, the wall-normal shear stress distribution in the liquid is given by
where ![]() $v$ is the vertical velocity,
$v$ is the vertical velocity, ![]() $x$ the wall-normal coordinate,
$x$ the wall-normal coordinate, ![]() $g$ the gravitational acceleration and
$g$ the gravitational acceleration and ![]() $\delta _l$ the film thickness. Clearly, the interfacial shear stress
$\delta _l$ the film thickness. Clearly, the interfacial shear stress ![]() $\tau _i$ (the second term on the right-hand side of (2.1)) must be
$\tau _i$ (the second term on the right-hand side of (2.1)) must be ![]() $\tau _i \sim \rho _l g \delta _l$ to significantly alter the hydrodynamics. The
$\tau _i \sim \rho _l g \delta _l$ to significantly alter the hydrodynamics. The ![]() $\tau _i$ in vertical annular flows has been studied experimentally in, for example, Belt, Van't Westende & Portela (Reference Belt, Van't Westende and Portela2009) and Mura & Gourdon (Reference Mura and Gourdon2017) and is typically modelled in the form
$\tau _i$ in vertical annular flows has been studied experimentally in, for example, Belt, Van't Westende & Portela (Reference Belt, Van't Westende and Portela2009) and Mura & Gourdon (Reference Mura and Gourdon2017) and is typically modelled in the form ![]() $\tau _i = C_f \rho _g V_g^2$ where
$\tau _i = C_f \rho _g V_g^2$ where ![]() $C_f$ is a friction factor and
$C_f$ is a friction factor and ![]() $V_g$ is the bulk gas velocity. Considering typical (in SI units) order of magnitudes
$V_g$ is the bulk gas velocity. Considering typical (in SI units) order of magnitudes ![]() $\rho _l=O(10^3)$,
$\rho _l=O(10^3)$, ![]() $g=O(10)$,
$g=O(10)$, ![]() $\delta _l = O(10^{-3})$,
$\delta _l = O(10^{-3})$, ![]() $\rho _g=O(1)$ and a relatively high estimate of
$\rho _g=O(1)$ and a relatively high estimate of ![]() $C_f=O(0.1)$ (observed for highly viscous fluids (Mura & Gourdon Reference Mura and Gourdon2017) but
$C_f=O(0.1)$ (observed for highly viscous fluids (Mura & Gourdon Reference Mura and Gourdon2017) but ![]() $C_f=O(0.01)$ for water), the
$C_f=O(0.01)$ for water), the ![]() $V_g = O(10)$ is required for
$V_g = O(10)$ is required for ![]() $\tau _i \sim \rho _l g \delta _l$. Here, we thus assume
$\tau _i \sim \rho _l g \delta _l$. Here, we thus assume ![]() $V_g$ sufficiently below such an estimate.
$V_g$ sufficiently below such an estimate.
We further assume any wall-normal heat transfer due to the flow in the circumferential direction of the tube negligible as compared with that caused by the flow in the wall-normal and vertical directions. In Åkesjö et al. (Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2018) the authors observed experimentally that the circumferential flow was much lower compared with the vertical one under relevant conditions and that it does not, therefore, significantly influence the liquid heat transfer.
The above-mentioned assumptions allow us to consider the problem as two-dimensional and to neglect the transport of mass across the interface due to evaporation. Still, we take into account the absorption of heat at the interface due to the latent heat of phase change that gives saturation conditions at the interface. A schematic illustration of the considered problem is shown in figure 1(b).
To compute average evaporative heat transfer rates, we consider statistically steady conditions (sufficiently far from the inlet) where all relevant statistics regarding the hydro- and thermodynamics of the film, such as the time-averaged temperature profile, film thickness ![]() $\delta _l$ and evaporation rate, are constant in the streamwise direction (Åkesjö et al. Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2018, Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2019). The streamwise position at which the statistics becomes constant generally depends on the governing parameters. Consequently, we compute our statistics on a number of uniformly distributed streamwise locations (typically 20–50) in the simulation domain. During postprocessing we can then assess if, and where, the statistics becomes constant. The presented data is only computed from the steady region of the domain (where we also remove the initial transient time series). For cases with a periodic domain, the statistics is by definition constant in the streamwise direction (at least when considering averages over at least one pitch length) although it takes a certain time to reach the statistically steady conditions. Here, we evaluate at what time the statistics becomes constant and remove the initial transient from the averaging data.
$\delta _l$ and evaporation rate, are constant in the streamwise direction (Åkesjö et al. Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2018, Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2019). The streamwise position at which the statistics becomes constant generally depends on the governing parameters. Consequently, we compute our statistics on a number of uniformly distributed streamwise locations (typically 20–50) in the simulation domain. During postprocessing we can then assess if, and where, the statistics becomes constant. The presented data is only computed from the steady region of the domain (where we also remove the initial transient time series). For cases with a periodic domain, the statistics is by definition constant in the streamwise direction (at least when considering averages over at least one pitch length) although it takes a certain time to reach the statistically steady conditions. Here, we evaluate at what time the statistics becomes constant and remove the initial transient from the averaging data.
At statistically steady conditions, the average wall heat flux ![]() $\bar {q}_{wall}$ is absorbed by the average evaporative heat flux
$\bar {q}_{wall}$ is absorbed by the average evaporative heat flux ![]() $\bar {q}_{evap}$ at the gas–liquid interface. The average heat transfer coefficient for evaporation
$\bar {q}_{evap}$ at the gas–liquid interface. The average heat transfer coefficient for evaporation ![]() $h_e$ can thus be defined as
$h_e$ can thus be defined as
For cases with surface modifications in an inlet–outlet domain, the evaporative heat flux ![]() $\bar {q}_{evap}$ is averaged over one pitch length
$\bar {q}_{evap}$ is averaged over one pitch length ![]() $\hat {p}$ to account for local variations around the modifications. In periodic domains,
$\hat {p}$ to account for local variations around the modifications. In periodic domains, ![]() $\bar {q}_{evap}$ is averaged over the entire domain. In this study, the
$\bar {q}_{evap}$ is averaged over the entire domain. In this study, the ![]() $h_e$ is always obtained at statistically steady conditions. The corresponding Nusselt number is commonly (and in this study) defined using a viscous length scale as (Schnabel Reference Schnabel2010)
$h_e$ is always obtained at statistically steady conditions. The corresponding Nusselt number is commonly (and in this study) defined using a viscous length scale as (Schnabel Reference Schnabel2010)
 \begin{equation} \mathit{Nu} = \frac{h_e}{k_l} \left(\frac{\nu_l^2}{g}\right)^{1/3},\end{equation}
\begin{equation} \mathit{Nu} = \frac{h_e}{k_l} \left(\frac{\nu_l^2}{g}\right)^{1/3},\end{equation}
where ![]() $\nu _l$ is the kinematic viscosity of the liquid and
$\nu _l$ is the kinematic viscosity of the liquid and ![]() $k_l$ is the thermal conductivity of the liquid.
$k_l$ is the thermal conductivity of the liquid.
2.1. Numerical framework
We use a multiphase DNS framework based on the volume of fluid (VOF) method which has been used extensively to resolve the complex hydro- and interfacial dynamics of falling films in other numerical works (Dietze et al. Reference Dietze, Leefken and Kneer2008; Doro & Aidun Reference Doro and Aidun2013; Albert, Marschall & Bothe Reference Albert, Marschall and Bothe2014; Åkesjö et al. Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2019).
We start by non-dimensionalising all variables using ![]() $\nu _l$,
$\nu _l$, ![]() $\rho _l$ and
$\rho _l$ and ![]() $g$. The non-dimensional variables are the spatial coordinates
$g$. The non-dimensional variables are the spatial coordinates ![]() $x^*_i = x_i/(\nu _l^2/g)^{1/3}$, velocity
$x^*_i = x_i/(\nu _l^2/g)^{1/3}$, velocity ![]() $u^*_i = u_i / (\nu _l g)^{1/3}$, time
$u^*_i = u_i / (\nu _l g)^{1/3}$, time ![]() $t^*= t/(\nu _l / g^2)^{1/3}$, density
$t^*= t/(\nu _l / g^2)^{1/3}$, density ![]() $\rho ^* = \rho /\rho _l$, dynamic viscosity
$\rho ^* = \rho /\rho _l$, dynamic viscosity ![]() $\mu ^* = \mu /(\nu _l \rho _l)$, pressure
$\mu ^* = \mu /(\nu _l \rho _l)$, pressure ![]() $p^* = p/(\rho _l (\nu _l^2/g)^{1/3} g )$, gravitational acceleration
$p^* = p/(\rho _l (\nu _l^2/g)^{1/3} g )$, gravitational acceleration ![]() $g_i^* = g_i/g$, interface curvature
$g_i^* = g_i/g$, interface curvature ![]() $\kappa ^* = \kappa / (g/\nu _l^2)^{1/3}$ and temperature
$\kappa ^* = \kappa / (g/\nu _l^2)^{1/3}$ and temperature ![]() $T^* = (T-T_{sat})/(T_{wall}-T_{sat})$. In the remainder of this paper, all variables are non-dimensionalised accordingly and the asterisk notation is hereafter omitted. The non-dimensional governing equations read
$T^* = (T-T_{sat})/(T_{wall}-T_{sat})$. In the remainder of this paper, all variables are non-dimensionalised accordingly and the asterisk notation is hereafter omitted. The non-dimensional governing equations read
where the term ![]() $1/\rho _r$ is only added in cases with a periodic domain to prevent the gas from accelerating in the gravitational direction,
$1/\rho _r$ is only added in cases with a periodic domain to prevent the gas from accelerating in the gravitational direction, ![]() $\boldsymbol{\mathsf{S}}=(\boldsymbol {\nabla }\boldsymbol {u} + \boldsymbol {\nabla }\boldsymbol {u}^{\rm T})/2$ is the rate of deformation tensor,
$\boldsymbol{\mathsf{S}}=(\boldsymbol {\nabla }\boldsymbol {u} + \boldsymbol {\nabla }\boldsymbol {u}^{\rm T})/2$ is the rate of deformation tensor, ![]() $\hat {\boldsymbol {n}}$ is the interface normal,
$\hat {\boldsymbol {n}}$ is the interface normal, ![]() $\delta _S$ is the Dirac distribution function that is only non-zero at the interface,
$\delta _S$ is the Dirac distribution function that is only non-zero at the interface, ![]() $\mathit {Ka} = \sigma / (g^{1/3}\nu _l^{4/3}\rho _l)$ is the Kapitza number (where
$\mathit {Ka} = \sigma / (g^{1/3}\nu _l^{4/3}\rho _l)$ is the Kapitza number (where ![]() $\sigma$ is the surface tension that we assume constant since the interfacial temperature is maintained at saturation conditions),
$\sigma$ is the surface tension that we assume constant since the interfacial temperature is maintained at saturation conditions), ![]() $f$ is the volume fraction field that is
$f$ is the volume fraction field that is ![]() $1$ in the liquid phase and
$1$ in the liquid phase and ![]() $0$ is the gas and
$0$ is the gas and ![]() $q_\mathit {evap}$ is the evaporative cooling term due to latent heat of phase change at the interface. The density is defined as
$q_\mathit {evap}$ is the evaporative cooling term due to latent heat of phase change at the interface. The density is defined as ![]() $\rho (f)=f+(1-f)(1/\rho _r)$, while the viscosity
$\rho (f)=f+(1-f)(1/\rho _r)$, while the viscosity ![]() $\mu (f)=(f+(1-f)\mu _r)^{-1}$ and thermal diffusivity
$\mu (f)=(f+(1-f)\mu _r)^{-1}$ and thermal diffusivity ![]() $D(f)=(f \mathit {Pr}_l+(1-f)\mathit {Pr}_g \mu _r/\rho _r)^{-1}$ are the harmonic means that are suitable approximations for gas–liquid interfaces (Tryggvason, Scardovelli & Zaleski Reference Tryggvason, Scardovelli and Zaleski2011). The liquid and gas Prandtl numbers are defined as
$D(f)=(f \mathit {Pr}_l+(1-f)\mathit {Pr}_g \mu _r/\rho _r)^{-1}$ are the harmonic means that are suitable approximations for gas–liquid interfaces (Tryggvason, Scardovelli & Zaleski Reference Tryggvason, Scardovelli and Zaleski2011). The liquid and gas Prandtl numbers are defined as ![]() $\mathit {Pr}_l = \nu _l/D_l$ and
$\mathit {Pr}_l = \nu _l/D_l$ and ![]() $\mathit {Pr}_g = \nu _g/D_g$, respectively, and the thermal diffusivities are
$\mathit {Pr}_g = \nu _g/D_g$, respectively, and the thermal diffusivities are ![]() $D_l=k_l/(\rho _l c_{p,l})$ and
$D_l=k_l/(\rho _l c_{p,l})$ and ![]() $D_g=k_g/(\rho _g c_{p,g})$.
$D_g=k_g/(\rho _g c_{p,g})$.
The total thermal resistance of the evaporating falling film can be considered as two resistances in series. The first one is the thermal resistance of the liquid film and the second one is the thermal resistance of the gas–liquid interface during evaporation due to molecular (kinetic) effects. By assuming saturation conditions in the gas and at the gas–liquid interface (the interface overheating is negligible as has been observed in our previous experiments (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023) and used in Schnabel (Reference Schnabel2010) and Kharangate, Lee & Mudawar (Reference Kharangate, Lee and Mudawar2015)), we implicitly assume that the thermal resistance of the liquid film dominates the total thermal resistance and that the evaporation rate, therefore, is limited by the rate at which heat is transported to the interface by the liquid. Consequently, the evaporation rate is not limited by kinetic effects at the interface.
In general, there exist neither a universally accepted evaporation model nor an implementation approach in two-phase flow problems involving phase change (Kharangate & Mudawar Reference Kharangate and Mudawar2017). A common model is the Rankine–Hugoniot jump conditions that neglects molecular (kinetic) effects and is generally used by assuming continuous interface saturation conditions (![]() $T_{l,{int}}=T_{g,{int}}=T_{sat}$) (thus assuming no interface resistance) (Gibou et al. Reference Gibou, Chen, Nguyen and Banerjee2007). The model is based on evaluating the net energy transfer across the interface as
$T_{l,{int}}=T_{g,{int}}=T_{sat}$) (thus assuming no interface resistance) (Gibou et al. Reference Gibou, Chen, Nguyen and Banerjee2007). The model is based on evaluating the net energy transfer across the interface as
where ![]() $k_l$ and
$k_l$ and ![]() $k_g$ are the thermal conductivity of the liquid and gas, respectively, and
$k_g$ are the thermal conductivity of the liquid and gas, respectively, and ![]() $\boldsymbol {\nabla } T$ is evaluated on either side of the interface. Since typically
$\boldsymbol {\nabla } T$ is evaluated on either side of the interface. Since typically ![]() $k_g \ll k_l$, this relation simplifies to
$k_g \ll k_l$, this relation simplifies to
suggesting that the evaporation rate is determined by the rate at which the liquid transports heat to the interface.
The evaporation rate can also be estimated using the model by Schrage (Reference Schrage1953) (based on the kinetic theory of gases) or the simplified and popular model of Tanasawa (Reference Tanasawa1991). These models take into account the additional thermal resistance at the interface, due to the kinetic effects. However, as long as this interface resistance is much smaller than the thermal resistance of the film, the specific model or model parameters do not significantly influence the results. The model by Tanasawa has the relatively simple functional form
where both phases are assumed at saturation conditions, but allows for a jump in temperature and pressure across the interface. The correct temperature boundary condition (BC) at the interface is still an unresolved issue (Juric & Tryggvason Reference Juric and Tryggvason1998) and neither (2.9) nor (2.10) are appropriate for all evaporative conditions. However, in the limit of small interfacial temperature jumps and small deviations from saturation conditions (thermal resistance of the interface is small), both models (2.9) and (2.10) predict the same evaporation rate since the rate predicted by both models is limited by the ability of the liquid to transport heat to the interface. In our DNS, we fully resolve this heat transport.
Since the Tanasawa model is more straightforward to implement into the VOF framework (as described in, for example, Hardt & Wondra (Reference Hardt and Wondra2008) and Kunkelmann (Reference Kunkelmann2011)), and has been successfully used to study evaporating films before (for example in the VOF methodology of Kharangate et al. (Reference Kharangate, Lee and Mudawar2015) and in the modelling framework of Sultan, Boudaoud & Amar (Reference Sultan, Boudaoud and Amar2005) that used the Hertz–Knudsen relation, which the Tanasawa model is based upon) we have chosen this model in our work.
To find a suitable model parameter ![]() $\alpha$ that gives negligible interfacial thermal resistance (introduced by the Tanasawa model), we consider the case of steady heat conduction in an evaporating laminar liquid film on a flat wall where
$\alpha$ that gives negligible interfacial thermal resistance (introduced by the Tanasawa model), we consider the case of steady heat conduction in an evaporating laminar liquid film on a flat wall where
Adding ![]() $(T_{int} - T_{sat})$ on both sides of (2.11) and rearranging we get
$(T_{int} - T_{sat})$ on both sides of (2.11) and rearranging we get
Using the non-dimensional formalism of the present paper this can be reformulated into
With typical values of ![]() $\delta ^*=O(10)$ and
$\delta ^*=O(10)$ and ![]() $Pr_l=O(10)$ in our cases, we obtain
$Pr_l=O(10)$ in our cases, we obtain
Here, we want ![]() $T^*_{int} \ll 1$ meaning that the temperature drop across the entire film
$T^*_{int} \ll 1$ meaning that the temperature drop across the entire film ![]() $(T_{wall}-T_{sat})$ is much larger than the temperature drop at the interface
$(T_{wall}-T_{sat})$ is much larger than the temperature drop at the interface ![]() $(T_{int}-T_{sat})$. Fulfilling these conditions thus implies that the interface resistance is indeed negligible. To maintain
$(T_{int}-T_{sat})$. Fulfilling these conditions thus implies that the interface resistance is indeed negligible. To maintain ![]() $T^*_{int} \ll 1$, (2.14) shows that
$T^*_{int} \ll 1$, (2.14) shows that ![]() $\alpha > 1$ is appropriate to obtain an interface temperature close to saturation conditions. For example, using
$\alpha > 1$ is appropriate to obtain an interface temperature close to saturation conditions. For example, using ![]() $\alpha = 100$ gives an interface temperature that deviates approximately
$\alpha = 100$ gives an interface temperature that deviates approximately ![]() $0.0001(T_{wall}-T_{sat})$ from the saturation temperature. In the present problem, the exact value of
$0.0001(T_{wall}-T_{sat})$ from the saturation temperature. In the present problem, the exact value of ![]() $\alpha$ is thus not important, it should just be large enough to achieve
$\alpha$ is thus not important, it should just be large enough to achieve ![]() $T_{int}\approx T_{sat}$ without causing numerical instabilities.
$T_{int}\approx T_{sat}$ without causing numerical instabilities.
To estimate an appropriate magnitude of ![]() $\alpha$, we use the idea that the local rate of heating at the interface should equal the local rate of cooling. Thus, an incremental increase of the interface temperature from
$\alpha$, we use the idea that the local rate of heating at the interface should equal the local rate of cooling. Thus, an incremental increase of the interface temperature from ![]() $T_{sat}$ to
$T_{sat}$ to ![]() $T_{int}$ gives
$T_{int}$ gives
where ![]() $n$ is the current computational time step and
$n$ is the current computational time step and ![]() $\Delta t$ is the time step size. We are aware of the fact that one could implement here a higher-order representation, but, we choose this simple form since it maintains
$\Delta t$ is the time step size. We are aware of the fact that one could implement here a higher-order representation, but, we choose this simple form since it maintains ![]() $T_{int} \approx T_{sat}$ in all our simulation cases without the need for parameter tuning or computing liquid temperature gradients normal to the interface. The representation (2.15) is therefore used in all our simulation cases.
$T_{int} \approx T_{sat}$ in all our simulation cases without the need for parameter tuning or computing liquid temperature gradients normal to the interface. The representation (2.15) is therefore used in all our simulation cases.
The time step ![]() $\Delta t$ is determined with the Courant–Friedrichs–Lewy (Courant number of 0.5) and the capillary time step criteria (Denner & van Wachem Reference Denner and van Wachem2015), where the latter criterion typically limits
$\Delta t$ is determined with the Courant–Friedrichs–Lewy (Courant number of 0.5) and the capillary time step criteria (Denner & van Wachem Reference Denner and van Wachem2015), where the latter criterion typically limits ![]() $\Delta t$ in our simulations to be within the range of
$\Delta t$ in our simulations to be within the range of ![]() $O(10^{-3}) - O(10^{-2})$. This gives a corresponding
$O(10^{-3}) - O(10^{-2})$. This gives a corresponding ![]() $\alpha =1/\Delta t$ in the range of approximately 100–1000. Additional simulations were also performed with a constant
$\alpha =1/\Delta t$ in the range of approximately 100–1000. Additional simulations were also performed with a constant ![]() $\alpha =500$, with practically no difference observed on the average heat transfer rates or interface temperature.
$\alpha =500$, with practically no difference observed on the average heat transfer rates or interface temperature.
Kharangate et al. (Reference Kharangate, Lee and Mudawar2015) also used the Tanasawa model to study turbulent evaporating falling films with the VOF method. To find a suitable ![]() $\alpha$ that maintains
$\alpha$ that maintains ![]() $T_{int} \approx T_{sat}$, the authors gradually increased the accommodation coefficient (included in
$T_{int} \approx T_{sat}$, the authors gradually increased the accommodation coefficient (included in ![]() $\alpha$) until
$\alpha$) until ![]() $(T_{int}-T_{sat})$ is minimised to an acceptable level. The end result is practically the same as ours.
$(T_{int}-T_{sat})$ is minimised to an acceptable level. The end result is practically the same as ours.
The falling film operating condition (here interpreted as the non-dimensional flow rate) is defined using the Reynolds number as
where ![]() $\varGamma$ is the mass flow rate of liquid per unit length of circumference,
$\varGamma$ is the mass flow rate of liquid per unit length of circumference, ![]() $\delta _l$ is the average film height and
$\delta _l$ is the average film height and ![]() $V_l$ is the average vertical velocity of the film. We fix the ratios
$V_l$ is the average vertical velocity of the film. We fix the ratios ![]() $\rho _r=1000$ and
$\rho _r=1000$ and ![]() $\mu _r =100$ that are relevant for industrial applications. The effects of these ratios are essentially negligible since their magnitudes indicate that the forces acting on the interface by the gas are small compared with the liquid (Kalliadasis et al. Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012). We also specify
$\mu _r =100$ that are relevant for industrial applications. The effects of these ratios are essentially negligible since their magnitudes indicate that the forces acting on the interface by the gas are small compared with the liquid (Kalliadasis et al. Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012). We also specify ![]() $\mathit {Pr}_g=0.7$ that is typical for gases. The effect of the latter parameter is also negligible since heat is only transported through the liquid film (from the wall and absorbed due to evaporation at the interface) whereas the gas phase is at uniform saturation conditions.
$\mathit {Pr}_g=0.7$ that is typical for gases. The effect of the latter parameter is also negligible since heat is only transported through the liquid film (from the wall and absorbed due to evaporation at the interface) whereas the gas phase is at uniform saturation conditions.
By fixing ![]() $\rho _r=1000$,
$\rho _r=1000$, ![]() $\mu _r =100$ and
$\mu _r =100$ and ![]() $\mathit {Pr}_g = 0.7$, we have the three governing fluid parameters
$\mathit {Pr}_g = 0.7$, we have the three governing fluid parameters ![]() $(\mathit {Ka},\mathit {Re},\mathit {Pr}_l)$ that, together with the surface topology parameters
$(\mathit {Ka},\mathit {Re},\mathit {Pr}_l)$ that, together with the surface topology parameters ![]() $(\hat {p},\hat {h},\hat {l})$, completely describe the hydro- and thermodynamics of the film. We thus consider the average heat transfer rate through the film as given by
$(\hat {p},\hat {h},\hat {l})$, completely describe the hydro- and thermodynamics of the film. We thus consider the average heat transfer rate through the film as given by ![]() $\mathit {Nu}_{smooth}(\mathit {Ka},\mathit {Re},\mathit {Pr}_l)$ on a smooth surface and
$\mathit {Nu}_{smooth}(\mathit {Ka},\mathit {Re},\mathit {Pr}_l)$ on a smooth surface and ![]() $\mathit {Nu}_{mod}(\mathit {Ka},\mathit {Re},\mathit {Pr}_l,\hat {p},\hat {h},\hat {l})$ on a modified surface.
$\mathit {Nu}_{mod}(\mathit {Ka},\mathit {Re},\mathit {Pr}_l,\hat {p},\hat {h},\hat {l})$ on a modified surface.
The governing equations (2.4)–(2.7) are solved in the open-source code Basilisk (Popinet Reference Popinet2015) that is widely used for DNS of gas–liquid interfacial flows (Dietze Reference Dietze2019; Lavalle et al. Reference Lavalle, Mergui, Grenier and Dietze2021; Boyd, Becker & Ling Reference Boyd, Becker and Ling2024). Here, the computational domain is always a square in two-dimensional. We specify the side length ![]() $L/\delta _N=O(100\unicode{x2013}1000)$ for our cases, where the Nusselt film thickness
$L/\delta _N=O(100\unicode{x2013}1000)$ for our cases, where the Nusselt film thickness ![]() $\delta _N$ is defined in (2.17). We adopt a cell-centred Cartesian tree-structured grid (square cells) and use an adaptive refinement technique that maintains a uniform resolution in the entire liquid film corresponding to the maximum specified refinement level. This gives a typical resolution of approximately 20–50 grid points per
$\delta _N$ is defined in (2.17). We adopt a cell-centred Cartesian tree-structured grid (square cells) and use an adaptive refinement technique that maintains a uniform resolution in the entire liquid film corresponding to the maximum specified refinement level. This gives a typical resolution of approximately 20–50 grid points per ![]() $\delta _N$ in our simulations, depending on the governing parameters. In the gas phase, the resolution gradually decreases to the minimum refinement level corresponding to 64 grid points per
$\delta _N$ in our simulations, depending on the governing parameters. In the gas phase, the resolution gradually decreases to the minimum refinement level corresponding to 64 grid points per ![]() $L$. With this grid configuration, a typical simulation requires
$L$. With this grid configuration, a typical simulation requires ![]() $O(10^5\unicode{x2013}10^6)$ grid points and runs on 32 cores for a few days. Statistically steady conditions are typically obtained after approximately 200 non-dimensional time units. The surface modifications are introduced on the left-hand wall of the domain using the embedded boundary methodology of Basilisk that follows the procedure in Johansen & Colella (Reference Johansen and Colella1998).
$O(10^5\unicode{x2013}10^6)$ grid points and runs on 32 cores for a few days. Statistically steady conditions are typically obtained after approximately 200 non-dimensional time units. The surface modifications are introduced on the left-hand wall of the domain using the embedded boundary methodology of Basilisk that follows the procedure in Johansen & Colella (Reference Johansen and Colella1998).
The system of equations is solved with a time-splitting projection method. The spatial gradients are discretised with standard second-order numerical schemes, and the velocity advection term with the Bell–Colella–Glaz second-order upwind scheme (Popinet Reference Popinet2003). The velocity and scalar fields are evolved in time with a staggered second-order method. The gas–liquid interface is reconstructed from the volume fraction field as a line in each computational cell containing the interface using the piecewise linear interface reconstruction method (Scardovelli & Zaleski Reference Scardovelli and Zaleski1999). This ensures that the interface is sharp and maintained within a single cell. The volume fraction field is then advected using geometric fluxes based on the reconstructed interface. Surface tension is accounted for using a well-balanced discretisation and an accurate height-function method is used to compute the interface curvature (Popinet Reference Popinet2018).
We use two different types of streamwise BCs in the computational domain. The first is termed an inlet–outlet domain and uses the laminar solution by Nusselt (Reference Nusselt1916) where the non-dimensional film thickness and mean velocity are given by
 \begin{gather}v_N = \left(\frac{\mathit{Re}^2}{3}\right)^{1/3}, \end{gather}
\begin{gather}v_N = \left(\frac{\mathit{Re}^2}{3}\right)^{1/3}, \end{gather}
respectively. At the top of the domain, we impose the inlet volume fraction ![]() $f(0{\leq } x {\leq } \delta _N)=1$ and
$f(0{\leq } x {\leq } \delta _N)=1$ and ![]() $f(\delta _N {<} x {\leq } L)=0$ and the velocity profile
$f(\delta _N {<} x {\leq } L)=0$ and the velocity profile
 \begin{gather} v(0{\leq} x {\leq} \delta_N) ={-}\frac{3}{2} v_N \left[2 \left(\frac{x}{\delta_N}\right) - \left(\frac{x}{\delta_N} \right)^2 \right ] [ 1+ \varepsilon \sin{(2{\rm \pi} f t)} ], \end{gather}
\begin{gather} v(0{\leq} x {\leq} \delta_N) ={-}\frac{3}{2} v_N \left[2 \left(\frac{x}{\delta_N}\right) - \left(\frac{x}{\delta_N} \right)^2 \right ] [ 1+ \varepsilon \sin{(2{\rm \pi} f t)} ], \end{gather}
where ![]() $\varepsilon =0.05$ is the perturbation amplitude and
$\varepsilon =0.05$ is the perturbation amplitude and ![]() $f=0.0261$ is the non-dimensional perturbation frequency. The perturbations are used to expedite fully developed conditions in the finite domain (Dietze et al. Reference Dietze, Leefken and Kneer2008; Denner et al. Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016; Åkesjö et al. Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2017). The specific value of the perturbation frequency is not expected to significantly influence our results since, for similar flow conditions on smooth surfaces, Åkesjö et al. (Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2017) showed that the developed wave dynamics converges for all the tested frequencies after sufficient length from the inlet (
$f=0.0261$ is the non-dimensional perturbation frequency. The perturbations are used to expedite fully developed conditions in the finite domain (Dietze et al. Reference Dietze, Leefken and Kneer2008; Denner et al. Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016; Åkesjö et al. Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2017). The specific value of the perturbation frequency is not expected to significantly influence our results since, for similar flow conditions on smooth surfaces, Åkesjö et al. (Reference Åkesjö, Gourdon, Vamling, Innings and Sasic2017) showed that the developed wave dynamics converges for all the tested frequencies after sufficient length from the inlet (![]() ${\approx }1000\delta _N$). In addition, on modified surfaces, (Åkesjö (Reference Åkesjö2018), figures 6–17) showed that the heat transfer from the wall to the film, at statistically steady conditions, is not related to the inlet perturbation frequency, but is instead dominated by the hydrodynamic fluctuations introduced by the surface modifications.
${\approx }1000\delta _N$). In addition, on modified surfaces, (Åkesjö (Reference Åkesjö2018), figures 6–17) showed that the heat transfer from the wall to the film, at statistically steady conditions, is not related to the inlet perturbation frequency, but is instead dominated by the hydrodynamic fluctuations introduced by the surface modifications.
The temperature BCs are ![]() $T=1$ at the wall,
$T=1$ at the wall, ![]() $T=0$ at the inlet and far-field, and symmetry at the outlet. The outlet is further specified as an open boundary with
$T=0$ at the inlet and far-field, and symmetry at the outlet. The outlet is further specified as an open boundary with ![]() $\partial u_i / \partial y = \partial p / \partial y = 0$ to allow the flow to exit with minimal reflections (Denner et al. Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016). The inlet BCs are used to initialise all fields in the domain. The inlet–outlet domain is used for all validation cases and comparisons with experiments (§§ 2.4 and 3.1) to allow the hydro- and thermodynamics of the film to develop over long streamwise distances.
$\partial u_i / \partial y = \partial p / \partial y = 0$ to allow the flow to exit with minimal reflections (Denner et al. Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016). The inlet BCs are used to initialise all fields in the domain. The inlet–outlet domain is used for all validation cases and comparisons with experiments (§§ 2.4 and 3.1) to allow the hydro- and thermodynamics of the film to develop over long streamwise distances.
In the second type of domain, we use periodic boundaries in the streamwise direction to compute and study average liquid heat fluxes at statistically steady conditions (in § 3.2) and to investigate the influence of important parameters on the total heat transfer rate (in § 3.3). The main advantage of the periodic domain is that the statistics is by definition constant in the entire domain (considering averages over at least one pitch length) although it takes a certain time to reach the statistically steady conditions. The periodic domains are also significantly smaller and thus computationally cheaper. This is opposed to the inlet–outlet domains where the domains are long and the statistics converges only after a sufficient length from the inlet that is not known a priori. For cases in a periodic domain, we evaluate at what time the statistics becomes constant and remove the initial transient from the averaging data. It should be noted that a periodic domain is only suitable for cases without solitary waves or where the wavelength of such waves is known and the domain length is selected appropriately. This is verified in our cases. The initial conditions in the periodic domain are the same as for the inlet–outlet domain except for the initial film thickness that is tuned to obtain the desired ![]() $\mathit {Re}$ number at statistically steady conditions. The inlet perturbations are here imposed at the top of the domain for an initial non-dimensional time
$\mathit {Re}$ number at statistically steady conditions. The inlet perturbations are here imposed at the top of the domain for an initial non-dimensional time ![]() $0\leq t\leq 40$ (approximately one flow-through time) and then stopped to again expedite fully developed conditions. Table 1 shows the domain type, non-dimensional parameters and results for all our simulation cases.
$0\leq t\leq 40$ (approximately one flow-through time) and then stopped to again expedite fully developed conditions. Table 1 shows the domain type, non-dimensional parameters and results for all our simulation cases.
Table 1. Non-dimensional parameters of the DNS. Cases starting with ‘S’ indicate a smooth heat transfer surface, ‘M’ is a modified surface and the ‘P’ refers to periodic BCs in the streamwise direction. Cases with in/outlet BCs have the Nusselt solution for velocity and volume fraction at the inlet and an open boundary at the outlet. All lengths are non-dimensionalised with the viscous length scale ![]() $(\nu _l^2/g)^{1/3}$ (or, if specified, related to the Nusselt film thickness
$(\nu _l^2/g)^{1/3}$ (or, if specified, related to the Nusselt film thickness ![]() $\delta _N$) and velocities with
$\delta _N$) and velocities with ![]() $(\nu _l g)^{1/3}$. The
$(\nu _l g)^{1/3}$. The ![]() $\mathit {Re}$,
$\mathit {Re}$, ![]() $\mathit {Ka}$ and
$\mathit {Ka}$ and ![]() $\mathit {Pr}_l$ (and the topology parameters for a modified surface; pitch
$\mathit {Pr}_l$ (and the topology parameters for a modified surface; pitch ![]() $\hat {p}$, height
$\hat {p}$, height ![]() $\hat {h}$ and length
$\hat {h}$ and length ![]() $\hat {l}$) determine the hydro- and thermodynamics of the falling film. The length of the computational domain
$\hat {l}$) determine the hydro- and thermodynamics of the falling film. The length of the computational domain ![]() $L$ is given in terms of
$L$ is given in terms of ![]() $\delta _N$ and the liquid grid resolution as the number of grid spacings
$\delta _N$ and the liquid grid resolution as the number of grid spacings ![]() $\varDelta$ per
$\varDelta$ per ![]() $\delta _N$. Here
$\delta _N$. Here ![]() $V_l$ is the average vertical (streamwise) film velocity,
$V_l$ is the average vertical (streamwise) film velocity, ![]() $\delta _l$ is the actual average film thickness and
$\delta _l$ is the actual average film thickness and ![]() $u_{l,{std}}$ is the standard deviation of the wall-normal liquid velocity fluctuations used in the definition of
$u_{l,{std}}$ is the standard deviation of the wall-normal liquid velocity fluctuations used in the definition of ![]() $\mathit {Pe}_l = u_{l,{std}} \delta _N / D_l$. The superscript
$\mathit {Pe}_l = u_{l,{std}} \delta _N / D_l$. The superscript ![]() $l$ represent values for the liquid phase.
$l$ represent values for the liquid phase.

2.2. Heat flux decomposition
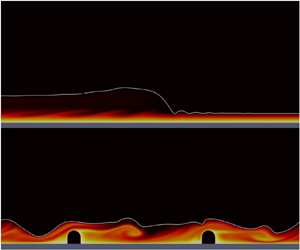
To understand the mechanisms behind the improved heat transfer (due to surface modifications), we first analyse instantaneous temperature fields to get a qualitative understanding of the influence of the surface modifications on the heat transfer through the film. Then, we compute average wall-normal heat fluxes in the film at statistically steady conditions to quantify the relative importance of the identified heat flux contributions and their spatial distribution. The heat fluxes in the film are decomposed into mean and fluctuating components to assess the influence of the altered mean flow and the hydrodynamic disturbances generated by the surface modifications. The averaging procedure is based on the methodology proposed in Loisy (Reference Loisy2016).
We start by defining the phase indicator function ![]() $H$ as
$H$ as
where ![]() $\varOmega _l$ is the liquid region and
$\varOmega _l$ is the liquid region and ![]() $\varOmega _g$ is the gas region of the domain.
$\varOmega _g$ is the gas region of the domain.
We are here interested in the heat transport through the liquid phase. For this purpose, we condition the general temperature transport equation (one-fluid formulation that is valid in both phases) with ![]() $H$ and use the relations
$H$ and use the relations ![]() $\partial H / \partial t + \boldsymbol {u} \boldsymbol {\cdot } \boldsymbol {\nabla } H = 0$,
$\partial H / \partial t + \boldsymbol {u} \boldsymbol {\cdot } \boldsymbol {\nabla } H = 0$, ![]() $\boldsymbol {\nabla } H = \delta _S\hat {\boldsymbol {n}}$ and the interface BC
$\boldsymbol {\nabla } H = \delta _S\hat {\boldsymbol {n}}$ and the interface BC ![]() $D_l\boldsymbol {\nabla } T \boldsymbol {\cdot } \hat {\boldsymbol {n}} \delta _S = q_{evap}\delta _S = q_{{evap},S}$ to obtain
$D_l\boldsymbol {\nabla } T \boldsymbol {\cdot } \hat {\boldsymbol {n}} \delta _S = q_{evap}\delta _S = q_{{evap},S}$ to obtain
that is still valid in both phases but non-zero only in the liquid phase. We define the ensemble average operator ![]() $\langle \ \rangle$ as
$\langle \ \rangle$ as ![]() $\langle G \rangle (\boldsymbol {x},t) = \int G(\boldsymbol {x},t:C)p(C)\,{\rm d} C$, where
$\langle G \rangle (\boldsymbol {x},t) = \int G(\boldsymbol {x},t:C)p(C)\,{\rm d} C$, where ![]() $G$ is a generic observable in configuration
$G$ is a generic observable in configuration ![]() $C$ and
$C$ and ![]() $p(C)$ is the probability density of configuration
$p(C)$ is the probability density of configuration ![]() $C$. The liquid ensemble averages are defined as
$C$. The liquid ensemble averages are defined as ![]() $\langle \boldsymbol {u}_l \rangle = \langle H\boldsymbol {u} \rangle (\boldsymbol {x},t)$ and
$\langle \boldsymbol {u}_l \rangle = \langle H\boldsymbol {u} \rangle (\boldsymbol {x},t)$ and ![]() $\langle T_l \rangle = \langle T \rangle (\boldsymbol {x},t)$, where we note that the non-dimensional temperature is non-zero only in the liquid phase (
$\langle T_l \rangle = \langle T \rangle (\boldsymbol {x},t)$, where we note that the non-dimensional temperature is non-zero only in the liquid phase (![]() $\langle T \rangle = \langle HT \rangle$). The liquid temperature and velocity fields are decomposed into fluctuating and mean values as
$\langle T \rangle = \langle HT \rangle$). The liquid temperature and velocity fields are decomposed into fluctuating and mean values as ![]() $T_l = T_l' + \langle T_l \rangle$ and
$T_l = T_l' + \langle T_l \rangle$ and ![]() $\boldsymbol {u}_l = \boldsymbol {u}_l' + \langle \boldsymbol {u}_l \rangle$. These relations are substituted into (2.23), which is then ensemble averaged. At fully developed (statistically steady) conditions
$\boldsymbol {u}_l = \boldsymbol {u}_l' + \langle \boldsymbol {u}_l \rangle$. These relations are substituted into (2.23), which is then ensemble averaged. At fully developed (statistically steady) conditions ![]() $\partial \langle HT \rangle / \partial t = 0$ and the resulting relation reads
$\partial \langle HT \rangle / \partial t = 0$ and the resulting relation reads
Using the definitions ![]() $\langle \boldsymbol {q'} \rangle _{l,{adv}}(\boldsymbol {x}) = \langle \boldsymbol {u}_l' T_l' \rangle$,
$\langle \boldsymbol {q'} \rangle _{l,{adv}}(\boldsymbol {x}) = \langle \boldsymbol {u}_l' T_l' \rangle$, ![]() $\langle \boldsymbol {q}\rangle _{l,{adv}}(\boldsymbol {x}) = \langle \boldsymbol {u}_l\rangle \langle T_l\rangle$,
$\langle \boldsymbol {q}\rangle _{l,{adv}}(\boldsymbol {x}) = \langle \boldsymbol {u}_l\rangle \langle T_l\rangle$, ![]() $\langle \boldsymbol {q'} \rangle _{l,{diff}}(\boldsymbol {x}) = -\langle H D_l \boldsymbol {\nabla } T_l' \rangle$ and
$\langle \boldsymbol {q'} \rangle _{l,{diff}}(\boldsymbol {x}) = -\langle H D_l \boldsymbol {\nabla } T_l' \rangle$ and ![]() $\langle \boldsymbol {q}\rangle _{l,{diff}}(\boldsymbol {x}) = -\langle H D_l \boldsymbol {\nabla } \langle T_l \rangle \rangle$, we get the relation
$\langle \boldsymbol {q}\rangle _{l,{diff}}(\boldsymbol {x}) = -\langle H D_l \boldsymbol {\nabla } \langle T_l \rangle \rangle$, we get the relation
where the heat flux contributions on the left-hand side represent, respectively: (i) advection of the temperature fluctuations by the liquid velocity fluctuations; (ii) advection of the mean temperature field by the mean velocity field; (iii) diffusive flux due to the temperature fluctuations; and (iv) diffusion of the mean temperature field.
At fully developed conditions, heat is only transported on average in the wall-normal direction, from the wall to the gas–liquid interface. To analyse the average contribution from each wall-normal heat flux through the film, we can thus average the wall-normal heat fluxes of (2.25) over the streamwise ![]() $y$-direction (the averaging is performed only in the fluid domain and not in the solid regions occupied by the surface modifications) as
$y$-direction (the averaging is performed only in the fluid domain and not in the solid regions occupied by the surface modifications) as ![]() $\langle {q} \rangle ^y_{l}(x) = 1/L_f \int _0^{L_f} \langle {q}\rangle _{l}(x,y)\,{{\rm d}y}$, where
$\langle {q} \rangle ^y_{l}(x) = 1/L_f \int _0^{L_f} \langle {q}\rangle _{l}(x,y)\,{{\rm d}y}$, where ![]() $L_f(x)$ is the streamwise length of the fluid domain (defined below) and where we denote the quantities averaged in the streamwise
$L_f(x)$ is the streamwise length of the fluid domain (defined below) and where we denote the quantities averaged in the streamwise ![]() $y$-direction with the superscript
$y$-direction with the superscript ![]() $y$. As discussed in § 2.1, the location of the fully developed region is not known a priori, and we use instead a periodic computational domain (which after an initial transient is inherently fully developed in the entire domain) to compute the average heat fluxes of (2.25).
$y$. As discussed in § 2.1, the location of the fully developed region is not known a priori, and we use instead a periodic computational domain (which after an initial transient is inherently fully developed in the entire domain) to compute the average heat fluxes of (2.25).
Equation (2.25) can now be rewritten in terms of the streamwise averaged quantities as
Integrating (2.26) from the wall (with the BC ![]() $\langle {q}\rangle ^y_{wall}$) to a location
$\langle {q}\rangle ^y_{wall}$) to a location ![]() $x$ gives the steady-state balance of heat fluxes into and out of the fluid domain as
$x$ gives the steady-state balance of heat fluxes into and out of the fluid domain as
where ![]() $\langle {q}\rangle ^y_{wall}(x)=Q_{wall}(x)/L_f(x)$ is the average wall heat flux into the fluid domain. Figure 2 illustrates the average heat flux balance at the position
$\langle {q}\rangle ^y_{wall}(x)=Q_{wall}(x)/L_f(x)$ is the average wall heat flux into the fluid domain. Figure 2 illustrates the average heat flux balance at the position ![]() $x$ in the fluid domain that is coloured in blue. The absorption of heat due to evaporative cooling occurs between the two wavy lines that represent the region in which the gas–liquid interface fluctuates (
$x$ in the fluid domain that is coloured in blue. The absorption of heat due to evaporative cooling occurs between the two wavy lines that represent the region in which the gas–liquid interface fluctuates (![]() $\langle q_{{evap},S} \rangle ^y$ is non-zero here). As the position
$\langle q_{{evap},S} \rangle ^y$ is non-zero here). As the position ![]() $x$ moves outwards into the latter region,
$x$ moves outwards into the latter region, ![]() $\langle q \rangle ^y_l (x)$ decreases and, beyond that region,
$\langle q \rangle ^y_l (x)$ decreases and, beyond that region, ![]() $\langle q \rangle ^y_l (x) = 0$ (all heat applied by the wall is absorbed by evaporation). The
$\langle q \rangle ^y_l (x) = 0$ (all heat applied by the wall is absorbed by evaporation). The ![]() $Q_{wall}(x)$ is the total heat flow rate applied to the fluid by the wall up to
$Q_{wall}(x)$ is the total heat flow rate applied to the fluid by the wall up to ![]() $x$ (along the red dashed line in figure 2) and
$x$ (along the red dashed line in figure 2) and ![]() $L_f(x)$ is the streamwise length of the fluid domain at
$L_f(x)$ is the streamwise length of the fluid domain at ![]() $x$ (length of the black dashed line where
$x$ (length of the black dashed line where ![]() $L_f(x{<}h) < L$ but
$L_f(x{<}h) < L$ but ![]() $L_f(x{>}h) = L$ due to the solid surface modifications that extend to
$L_f(x{>}h) = L$ due to the solid surface modifications that extend to ![]() $x=h$). The
$x=h$). The ![]() $\langle {q}\rangle ^y_{wall}(x)$ thereby varies for
$\langle {q}\rangle ^y_{wall}(x)$ thereby varies for ![]() $x \leq h$ because of the surface modifications (that contribute to
$x \leq h$ because of the surface modifications (that contribute to ![]() $Q_{wall}(x)$ and alter
$Q_{wall}(x)$ and alter ![]() $L_f(x)$). At
$L_f(x)$). At ![]() $x>h$,
$x>h$, ![]() $\langle {q}\rangle ^y_{wall}(x)$ is positive and constant. The term
$\langle {q}\rangle ^y_{wall}(x)$ is positive and constant. The term ![]() $\langle {q}\rangle ^y_{evap}(x)=Q_{evap}(x)/L_f(x)$ represents the average heat flux out of the fluid domain due to evaporation until location
$\langle {q}\rangle ^y_{evap}(x)=Q_{evap}(x)/L_f(x)$ represents the average heat flux out of the fluid domain due to evaporation until location ![]() $x$ where
$x$ where ![]() $Q_{evap}(x)=\int _0^x \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}'$. The left-hand side of (2.27) represents the contributions to the total heat flux
$Q_{evap}(x)=\int _0^x \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}'$. The left-hand side of (2.27) represents the contributions to the total heat flux ![]() $\langle q \rangle ^y_l (x)$ (the sum of the left-hand side) through the liquid at position
$\langle q \rangle ^y_l (x)$ (the sum of the left-hand side) through the liquid at position ![]() $x$.
$x$.

Figure 2. Schematic illustration of the average heat fluxes through the liquid film. The blue region represents the fluid domain up to position ![]() $x$ and the two blue wavy lines indicate the interface region in which the evaporative cooling takes place. The latter region is thus where the gas–liquid interface fluctuates. The red dashed line represents the total wall length
$x$ and the two blue wavy lines indicate the interface region in which the evaporative cooling takes place. The latter region is thus where the gas–liquid interface fluctuates. The red dashed line represents the total wall length ![]() $L_{wall}(x)$ up to position
$L_{wall}(x)$ up to position ![]() $x$ and the black dashed line is the length of the fluid domain
$x$ and the black dashed line is the length of the fluid domain ![]() $L_f(x)$ at
$L_f(x)$ at ![]() $x$. The red arrows represent heat flux from the wall to the fluid, the blue arrows are the heat flux through the fluid domain at
$x$. The red arrows represent heat flux from the wall to the fluid, the blue arrows are the heat flux through the fluid domain at ![]() $x$ and the green arrows represent heat flux out of the fluid domain due to evaporation. According to (2.27), the total average heat flux
$x$ and the green arrows represent heat flux out of the fluid domain due to evaporation. According to (2.27), the total average heat flux ![]() $\langle q \rangle ^y_l(x)$ through the fluid domain at a position
$\langle q \rangle ^y_l(x)$ through the fluid domain at a position ![]() $x$ (black dashed line) equals the difference between the wall heat flux up to
$x$ (black dashed line) equals the difference between the wall heat flux up to ![]() $x$ (
$x$ (![]() $\langle {q}\rangle ^y_{wall}(x) = Q_{wall}(x)/L_f(x)$ representing the wall heat flow rate along the red dashed line) and the average evaporative heat flux out of the domain (
$\langle {q}\rangle ^y_{wall}(x) = Q_{wall}(x)/L_f(x)$ representing the wall heat flow rate along the red dashed line) and the average evaporative heat flux out of the domain (![]() $\langle {q}\rangle ^y_{evap}(x)=\int _0^x \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}' / L_f(x)$).
$\langle {q}\rangle ^y_{evap}(x)=\int _0^x \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}' / L_f(x)$).
Using (2.25) and (2.27), we quantify the different modes of heat transfer within the liquid film and determine the governing mechanisms behind the heat transfer improvement due to surface modifications. First, however, we start by validating our numerical framework.
2.3. Grid independence study
To capture the governing hydro- and thermodynamics of the problem, all relevant scales must be resolved. Because of the relatively high ![]() $\mathit {Pr}_l=O(10)$ in the present problem, we expect the smallest thermal scales to dictate the required grid resolution. To determine the necessary resolution in the liquid film, we define a test case with a modified surface and a high
$\mathit {Pr}_l=O(10)$ in the present problem, we expect the smallest thermal scales to dictate the required grid resolution. To determine the necessary resolution in the liquid film, we define a test case with a modified surface and a high ![]() $\mathit {Pr}_l=20$ where we expect the thermal scales to be minimal (of the cases considered in this study). The fluid parameters are
$\mathit {Pr}_l=20$ where we expect the thermal scales to be minimal (of the cases considered in this study). The fluid parameters are ![]() $\mathit {Ka}=488$ and
$\mathit {Ka}=488$ and ![]() $\mathit {Re}=100$ and the surface topology parameters (illustrated in figure 1a) are
$\mathit {Re}=100$ and the surface topology parameters (illustrated in figure 1a) are ![]() $\hat {p}=10\delta _N$ and
$\hat {p}=10\delta _N$ and ![]() $\hat {h}=\hat {l}=\delta _N$ with the Nusselt film thickness
$\hat {h}=\hat {l}=\delta _N$ with the Nusselt film thickness ![]() $\delta _N$ defined in (2.17).
$\delta _N$ defined in (2.17).
We use a periodic square domain of side length ![]() $L=80\delta _N$,
$L=80\delta _N$, ![]() $T_{wall}=1$ and we initialise the temperature field with
$T_{wall}=1$ and we initialise the temperature field with ![]() $T=0$. Once the average temperature and the
$T=0$. Once the average temperature and the ![]() $\mathit {Re}$ number of the film have reached statistically steady values we compute the average
$\mathit {Re}$ number of the film have reached statistically steady values we compute the average ![]() $\mathit {Nu}$-value and wall-normal temperature profile over the domain. This is done for grid resolutions from
$\mathit {Nu}$-value and wall-normal temperature profile over the domain. This is done for grid resolutions from ![]() $6$ to
$6$ to ![]() $51\varDelta / \delta _N$ (achieved by increasing the maximum refinement level in the adaptive grid method that maintains the maximum level in the entire film). Figure 3(a) shows that
$51\varDelta / \delta _N$ (achieved by increasing the maximum refinement level in the adaptive grid method that maintains the maximum level in the entire film). Figure 3(a) shows that ![]() $\mathit {Nu}$ decreases from
$\mathit {Nu}$ decreases from ![]() $0.66$ at
$0.66$ at ![]() $6 \varDelta /\delta _N$ to
$6 \varDelta /\delta _N$ to ![]() $0.53$ at
$0.53$ at ![]() $51 \varDelta / \delta _N$. There is, however, only a
$51 \varDelta / \delta _N$. There is, however, only a ![]() $4\,\%$ difference between the two highest resolution cases indicating
$4\,\%$ difference between the two highest resolution cases indicating ![]() $26 \varDelta / \delta _N$ is a sufficient resolution. This is further justified by the average temperature profiles shown in figure 3(b). Here, the two highest resolution cases are almost identical while the lower resolution cases underestimate the temperature close to the wall. The surface modifications extend to
$26 \varDelta / \delta _N$ is a sufficient resolution. This is further justified by the average temperature profiles shown in figure 3(b). Here, the two highest resolution cases are almost identical while the lower resolution cases underestimate the temperature close to the wall. The surface modifications extend to ![]() $x=\delta _N$ and, after that, the average temperature drops rapidly to saturation conditions
$x=\delta _N$ and, after that, the average temperature drops rapidly to saturation conditions ![]() $T=0$ at approximately
$T=0$ at approximately ![]() $x=2\delta _N$. In summary, approximately
$x=2\delta _N$. In summary, approximately ![]() $25 \varDelta / \delta _N$ suffice for
$25 \varDelta / \delta _N$ suffice for ![]() $\mathit {Pr}_l = 20$ while a slightly lower resolution is most likely adequate for lower
$\mathit {Pr}_l = 20$ while a slightly lower resolution is most likely adequate for lower ![]() $\mathit {Pr}_l$ numbers.
$\mathit {Pr}_l$ numbers.

Figure 3. Grid independence study on the case with (![]() $\mathit {Ka}=488, \mathit {Re}=100, \mathit {Pr}_l = 20$) on a modified surface with the topology parameters
$\mathit {Ka}=488, \mathit {Re}=100, \mathit {Pr}_l = 20$) on a modified surface with the topology parameters ![]() $p=10\delta _N, h=l=\delta _N$. The domain is a periodic square with length
$p=10\delta _N, h=l=\delta _N$. The domain is a periodic square with length ![]() $L=80\delta _N$ and
$L=80\delta _N$ and ![]() $T_{wall}=1$. (a) Average
$T_{wall}=1$. (a) Average ![]() $\mathit {Nu}$ number at statistically steady state converging with increasing resolution. (b) Average non-dimensional temperature profiles in the wall-normal direction. Also here the two highest resolution cases are almost identical indicating approximately
$\mathit {Nu}$ number at statistically steady state converging with increasing resolution. (b) Average non-dimensional temperature profiles in the wall-normal direction. Also here the two highest resolution cases are almost identical indicating approximately ![]() $25 \varDelta / \delta _N$ is sufficient at
$25 \varDelta / \delta _N$ is sufficient at ![]() $\mathit {Pr}_l = 20$.
$\mathit {Pr}_l = 20$.
2.4. Validation for smooth surfaces
We now validate our numerical framework against existing experimental correlations and measurements on smooth surfaces. We choose fluid parameters relevant in, for example, the paper and pulp industry as ![]() $\mathit {Ka}=488$ and
$\mathit {Ka}=488$ and ![]() $\mathit {Pr}_l = 12.4$ (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). The
$\mathit {Pr}_l = 12.4$ (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). The ![]() $\mathit {Re}$ number is varied in the range 15–530 (Cases S1–5) where we have existing measurements on a pilot scale evaporator by Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023), experimental correlations by Numrich (Reference Numrich1995) and, more recently, by Gourdon et al. (Reference Gourdon, Karlsson, Innings, Jongsma and Vamling2016). The correlations are based on a combination of laminar and turbulent parts as in Schnabel (Reference Schnabel2010) and Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023), and read
$\mathit {Re}$ number is varied in the range 15–530 (Cases S1–5) where we have existing measurements on a pilot scale evaporator by Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023), experimental correlations by Numrich (Reference Numrich1995) and, more recently, by Gourdon et al. (Reference Gourdon, Karlsson, Innings, Jongsma and Vamling2016). The correlations are based on a combination of laminar and turbulent parts as in Schnabel (Reference Schnabel2010) and Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023), and read
A close-up snapshot from Case S3 with ![]() $\mathit {Re}=90$ is shown in figure 4. For reference,
$\mathit {Re}=90$ is shown in figure 4. For reference, ![]() $\mathit {Re}=90$ corresponds to
$\mathit {Re}=90$ corresponds to ![]() $\delta _N=0.43$ mm for the industrially relevant fluid in (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023) with
$\delta _N=0.43$ mm for the industrially relevant fluid in (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023) with ![]() $\nu _l = 1.7 \times 10^{-6}\,{\rm m}^2\,{\rm s}^{-1}$. Here, the film flows from left to right and the horizontal axis is scaled by
$\nu _l = 1.7 \times 10^{-6}\,{\rm m}^2\,{\rm s}^{-1}$. Here, the film flows from left to right and the horizontal axis is scaled by ![]() $0.1$ to visualise the long waves. The gas–liquid interface is shown as a thick grey line that outlines two solitary waves. The colours represent the temperature field at the same instant. Here, it is clear that the internal wave dynamics disturbs the thermal boundary layer leading to increased mixing and heat transfer. We also note that the evaporative cooling model maintains saturation temperature
$0.1$ to visualise the long waves. The gas–liquid interface is shown as a thick grey line that outlines two solitary waves. The colours represent the temperature field at the same instant. Here, it is clear that the internal wave dynamics disturbs the thermal boundary layer leading to increased mixing and heat transfer. We also note that the evaporative cooling model maintains saturation temperature ![]() $T=0$ at the interface and in the gas phase.
$T=0$ at the interface and in the gas phase.

Figure 4. Snapshot from a section of the non-dimensional temperature field in an evaporating falling film (Case S3 with ![]() $\mathit {Ka}=488, \mathit {Pr}_l=12.4, \mathit {Re}=90$) on a smooth wall The liquid is below the gas–liquid interface (thick grey line) and flows from left to right. Note that the horizontal axis (but not the vertical) is scaled by
$\mathit {Ka}=488, \mathit {Pr}_l=12.4, \mathit {Re}=90$) on a smooth wall The liquid is below the gas–liquid interface (thick grey line) and flows from left to right. Note that the horizontal axis (but not the vertical) is scaled by ![]() $0.1$ for visualisation purposes, thus altering the aspect ratio. Here
$0.1$ for visualisation purposes, thus altering the aspect ratio. Here ![]() $T=0$ equals the non-dimensional saturation temperature that is maintained at the interface and in the gas phase by the evaporative cooling model. The internal wave hydrodynamics induces mixing of the thermal boundary layer and thereby enhances the heat transfer rate.
$T=0$ equals the non-dimensional saturation temperature that is maintained at the interface and in the gas phase by the evaporative cooling model. The internal wave hydrodynamics induces mixing of the thermal boundary layer and thereby enhances the heat transfer rate.
We compute the ![]() $\mathit {Nu}$ number at statistically steady conditions with the result shown in figure 5. Here, we observe an excellent match to the existing correlations and within the error margin of the pilot scale evaporator measurements. These validation cases show that our numerical framework accurately captures the governing hydro- and thermodynamic phenomena of the problem under industrially relevant conditions.
$\mathit {Nu}$ number at statistically steady conditions with the result shown in figure 5. Here, we observe an excellent match to the existing correlations and within the error margin of the pilot scale evaporator measurements. These validation cases show that our numerical framework accurately captures the governing hydro- and thermodynamic phenomena of the problem under industrially relevant conditions.

Figure 5. Validation of the predicted average heat transfer rate ![]() $\mathit {Nu}$ for an evaporative falling film on a smooth surface. The fluid parameters are
$\mathit {Nu}$ for an evaporative falling film on a smooth surface. The fluid parameters are ![]() $\mathit {Ka}=488$ and
$\mathit {Ka}=488$ and ![]() $\mathit {Pr}_l=12.4$ and we vary the
$\mathit {Pr}_l=12.4$ and we vary the ![]() $\mathit {Re}$ number from
$\mathit {Re}$ number from ![]() $15$ to
$15$ to ![]() $530$ (Cases S1–S5). The predictions are in excellent agreement with relevant correlations from the literature and within the error margin of the measurements from a pilot scale evaporator presented in Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023).
$530$ (Cases S1–S5). The predictions are in excellent agreement with relevant correlations from the literature and within the error margin of the measurements from a pilot scale evaporator presented in Åkesjö et al. (Reference Åkesjö, Gourdon, Jongsma and Sasic2023).
3. Results
In this section we present our results from the simulations of evaporative falling films on modified surfaces. We start by analysing the improvement of the total heat transfer rate for industrially relevant cases where we can compare with existing measurements from the pilot scale evaporator (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). Based on these results, we select a base case to analyse the average heat fluxes through the liquid film. With the latter case, we also investigate the dependence of surface topology parameters and the ![]() $\mathit {Pr}_l$ number on the heat transfer.
$\mathit {Pr}_l$ number on the heat transfer.
3.1. Predicted heat transfer rate on modified surfaces at industrially relevant conditions
Here, we investigate the average heat transfer rate on a modified surface similar to the one used in the existing measurements on the pilot scale evaporator (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023) at industrially relevant conditions. The simulation set-up and fluid parameters (![]() $\mathit {Ka}=488, \mathit {Pr}_l = 12.4$) are the same as for the smooth surface described in § 2.4, but here we add surface modification with the non-dimensional topology parameters
$\mathit {Ka}=488, \mathit {Pr}_l = 12.4$) are the same as for the smooth surface described in § 2.4, but here we add surface modification with the non-dimensional topology parameters ![]() $\hat {p}=180$ and
$\hat {p}=180$ and ![]() $\hat {h}=\hat {l}=15$ (Cases M1–5). This methodology allows us to quantify the heat transfer improvement due to surface modifications compared with the cases with a smooth surface.
$\hat {h}=\hat {l}=15$ (Cases M1–5). This methodology allows us to quantify the heat transfer improvement due to surface modifications compared with the cases with a smooth surface.
Figure 6 shows the instantaneous temperature field in the film for Case M2 with a modified surface and the parameters ![]() $\mathit {Ka}=488, \mathit {Pr}_l=12.4$ and
$\mathit {Ka}=488, \mathit {Pr}_l=12.4$ and ![]() $\mathit {Re}=90$ that correspond to the Case S3 shown in figure 4 on a smooth surface. Note that the horizontal axis of the former figure is scaled by
$\mathit {Re}=90$ that correspond to the Case S3 shown in figure 4 on a smooth surface. Note that the horizontal axis of the former figure is scaled by ![]() $0.2$. Comparing the two cases qualitatively, the surface modifications clearly induce significant hydrodynamic and thermal fluctuations in the majority of the film, while such disturbances are only observed in the solitary waves on smooth surfaces. The modifications are thus expected to enhance mixing and the average heat transport through the film. In the next section, we quantify and analyse the average heat flux contributions in detail.
$0.2$. Comparing the two cases qualitatively, the surface modifications clearly induce significant hydrodynamic and thermal fluctuations in the majority of the film, while such disturbances are only observed in the solitary waves on smooth surfaces. The modifications are thus expected to enhance mixing and the average heat transport through the film. In the next section, we quantify and analyse the average heat flux contributions in detail.

Figure 6. Snapshot from a section of the non-dimensional temperature field in an evaporating falling film (Case M2 with ![]() $\mathit {Ka}=488, \mathit {Pr}_l=12.4, \mathit {Re}=90$) on a modified surface in an inlet–outlet domain. Note that the horizontal axis (but not the vertical) is scaled by
$\mathit {Ka}=488, \mathit {Pr}_l=12.4, \mathit {Re}=90$) on a modified surface in an inlet–outlet domain. Note that the horizontal axis (but not the vertical) is scaled by ![]() $0.2$ for visualisation purposes, thus altering the aspect ratio. The liquid is below the gas–liquid interface (thick grey line) and flows from left to right. Here
$0.2$ for visualisation purposes, thus altering the aspect ratio. The liquid is below the gas–liquid interface (thick grey line) and flows from left to right. Here ![]() $T=0$ equals the non-dimensional saturation temperature that is maintained at the interface and in the gas phase by the evaporative cooling model. The surface modifications induce significant mixing of the thermal boundary layer and thereby enhance the heat transfer rate.
$T=0$ equals the non-dimensional saturation temperature that is maintained at the interface and in the gas phase by the evaporative cooling model. The surface modifications induce significant mixing of the thermal boundary layer and thereby enhance the heat transfer rate.
Figure 7 shows the predicted ![]() $\mathit {Nu}$ numbers on modified surfaces (Cases M1–5), the corresponding experimental data (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023) and the results on smooth surfaces (Cases S1–5) presented in figure 5. Our predicted
$\mathit {Nu}$ numbers on modified surfaces (Cases M1–5), the corresponding experimental data (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023) and the results on smooth surfaces (Cases S1–5) presented in figure 5. Our predicted ![]() $\mathit {Nu}$ numbers show a heat transfer improvement
$\mathit {Nu}$ numbers show a heat transfer improvement ![]() $(\mathit {Nu}_{mod} - \mathit {Nu}_{smooth}) / \mathit {Nu}_{smooth}$ of approximately 75 %–175 % in the range of
$(\mathit {Nu}_{mod} - \mathit {Nu}_{smooth}) / \mathit {Nu}_{smooth}$ of approximately 75 %–175 % in the range of ![]() $\mathit {Re}=50$ to
$\mathit {Re}=50$ to ![]() $545$. This is in fair agreement with the improvement seen in the experiments on the pilot scale evaporator (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). It should, however, be noted that, in the experiments, the authors observed high velocity cocurrent vapour flows that gave significant pressure drops along the tube (and consequently altered the local saturation temperature and heat transfer rate). In the same study, a heat flux dependence was noticed on the measured heat transfer coefficients that was not fully investigated. These phenomena were most significant for modified surfaces where the heat transfer rates were the highest and this complicates a direct quantitative comparison with our simulations. Still, our results for modified surfaces are in fair quantitative agreement and show similar trends as observed in the experiments. Therefore, we are confident that the governing physical phenomena and heat transfer mechanisms of the problem are predicted correctly.
$545$. This is in fair agreement with the improvement seen in the experiments on the pilot scale evaporator (Åkesjö et al. Reference Åkesjö, Gourdon, Jongsma and Sasic2023). It should, however, be noted that, in the experiments, the authors observed high velocity cocurrent vapour flows that gave significant pressure drops along the tube (and consequently altered the local saturation temperature and heat transfer rate). In the same study, a heat flux dependence was noticed on the measured heat transfer coefficients that was not fully investigated. These phenomena were most significant for modified surfaces where the heat transfer rates were the highest and this complicates a direct quantitative comparison with our simulations. Still, our results for modified surfaces are in fair quantitative agreement and show similar trends as observed in the experiments. Therefore, we are confident that the governing physical phenomena and heat transfer mechanisms of the problem are predicted correctly.

Figure 7. Predicted average heat transfer rates ![]() $\mathit {Nu}$ for evaporative falling films on smooth and modified surfaces (Case S1–5 and M1–5). The fluid parameters are
$\mathit {Nu}$ for evaporative falling films on smooth and modified surfaces (Case S1–5 and M1–5). The fluid parameters are ![]() $\mathit {Ka}=488$ and
$\mathit {Ka}=488$ and ![]() $\mathit {Pr}_l=12.4$ except for the two highest
$\mathit {Pr}_l=12.4$ except for the two highest ![]() $\mathit {Re}$ number cases on modified surfaces where we increase
$\mathit {Re}$ number cases on modified surfaces where we increase ![]() $\mathit {Ka}=5000$ (Cases M4 and M5) to prevent numerical issues due to sputtering and entrainment of bubbles.
$\mathit {Ka}=5000$ (Cases M4 and M5) to prevent numerical issues due to sputtering and entrainment of bubbles.
At ![]() $\mathit {Re} \gtrapprox 100$, the surface modifications induce sufficient hydrodynamic disturbances that generate sputtering (detachment of liquid ligaments) and entrainment of bubbles. Figure 8 shows an example of such events for Case M3 with
$\mathit {Re} \gtrapprox 100$, the surface modifications induce sufficient hydrodynamic disturbances that generate sputtering (detachment of liquid ligaments) and entrainment of bubbles. Figure 8 shows an example of such events for Case M3 with ![]() $\mathit {Re} = 215$. These events are preferably avoided in real applications but also cause numerical instabilities in our simulations at even higher
$\mathit {Re} = 215$. These events are preferably avoided in real applications but also cause numerical instabilities in our simulations at even higher ![]() $\mathit {Re}$ numbers (in Case M3 these problems diminish farther downstream and we manage to obtain a statistically steady region). The instabilities are probably due to the formation of very thin fluid regions (of the order of a single computational cell) and unrealistic evaporative cooling rates at the bubble interfaces predicted by the evaporative cooling model (for example in under-resolved thin liquid films between the bubble and the wall and at the three-phase contact line that can cause very high local cooling rates in the cells at the wall due to the wall Dirichlet temperature BCs). To avoid these problems and show the correct trend of the
$\mathit {Re}$ numbers (in Case M3 these problems diminish farther downstream and we manage to obtain a statistically steady region). The instabilities are probably due to the formation of very thin fluid regions (of the order of a single computational cell) and unrealistic evaporative cooling rates at the bubble interfaces predicted by the evaporative cooling model (for example in under-resolved thin liquid films between the bubble and the wall and at the three-phase contact line that can cause very high local cooling rates in the cells at the wall due to the wall Dirichlet temperature BCs). To avoid these problems and show the correct trend of the ![]() $\mathit {Nu}$ numbers, we increase the surface tension by a factor of
$\mathit {Nu}$ numbers, we increase the surface tension by a factor of ![]() $10$ for the two highest
$10$ for the two highest ![]() $\mathit {Re}$ number cases (Cases M4 and M5 with
$\mathit {Re}$ number cases (Cases M4 and M5 with ![]() $\mathit {Re}=360$ and
$\mathit {Re}=360$ and ![]() $530$, respectively) with modified surfaces presented in figure 7. We then get the predicted
$530$, respectively) with modified surfaces presented in figure 7. We then get the predicted ![]() $Nu$-trend in fair agreement to the experiments also for the highest
$Nu$-trend in fair agreement to the experiments also for the highest ![]() $\mathit {Re}$ numbers. Indeed, the influence of
$\mathit {Re}$ numbers. Indeed, the influence of ![]() $\mathit {Ka}$ on
$\mathit {Ka}$ on ![]() $\mathit {Nu}$ is relatively weak and often neglected (Schnabel Reference Schnabel2010) as is indicated by the
$\mathit {Nu}$ is relatively weak and often neglected (Schnabel Reference Schnabel2010) as is indicated by the ![]() $\mathit {Nu}$-correlations in (2.28) and (2.29). This is further corroborated in the work of Al-Sibai (Reference Al-Sibai2006) where phase-boundaries between hydrodynamics regimes scale approximately as
$\mathit {Nu}$-correlations in (2.28) and (2.29). This is further corroborated in the work of Al-Sibai (Reference Al-Sibai2006) where phase-boundaries between hydrodynamics regimes scale approximately as ![]() $\mathit {Re} \propto \mathit {Ka}^{0.3}$ indicating relatively weak influence of
$\mathit {Re} \propto \mathit {Ka}^{0.3}$ indicating relatively weak influence of ![]() $\mathit {Ka}$ on the characteristic hydrodynamics.
$\mathit {Ka}$ on the characteristic hydrodynamics.

Figure 8. Snapshot of the volume fraction field close to the inlet for an evaporating falling film (Case M3 with ![]() $\mathit {Ka}=488, \mathit {Re}=215$) on a modified surface. The liquid flows from left to right with the domain inlet at the left-hand edge. Note that the horizontal axis (but not the vertical) is scaled by
$\mathit {Ka}=488, \mathit {Re}=215$) on a modified surface. The liquid flows from left to right with the domain inlet at the left-hand edge. Note that the horizontal axis (but not the vertical) is scaled by ![]() $0.5$ for visualisation purposes, thus altering the aspect ratio. The black colour represents the gas phase, red the liquid and grey is the surface modifications. Sputtering events (detachment of liquid ligaments) and entrainment of bubbles appear at this
$0.5$ for visualisation purposes, thus altering the aspect ratio. The black colour represents the gas phase, red the liquid and grey is the surface modifications. Sputtering events (detachment of liquid ligaments) and entrainment of bubbles appear at this ![]() $\mathit {Re}$ number and become even more frequent at higher values of
$\mathit {Re}$ number and become even more frequent at higher values of ![]() $\mathit {Re}$.
$\mathit {Re}$.
In our simulations with surface modifications (Cases M1–5), we did not observe any large-amplitude waves resembling the solitary waves developing on the smooth surface. On the modified surface, such waves would inevitably interact with the modifications and other hydrodynamic fluctuations and not have a constant shape in the reference frame of the wave, as on the smooth surface. The absence of such waves facilitates the use of periodic domains in our subsequent analyses of the heat fluxes in the film. At ![]() $\mathit {Re}=90$, the predicted
$\mathit {Re}=90$, the predicted ![]() $\mathit {Nu}$ number on the modified surface differs only
$\mathit {Nu}$ number on the modified surface differs only ![]() $0.02$ when using an inlet–outlet domain and a periodic domain of
$0.02$ when using an inlet–outlet domain and a periodic domain of ![]() $L=8p$ (as explained in § 2.1). This shows that the use of a periodic domain is appropriate under these conditions and can therefore be used to analyse the heat transfer mechanisms in the next section.
$L=8p$ (as explained in § 2.1). This shows that the use of a periodic domain is appropriate under these conditions and can therefore be used to analyse the heat transfer mechanisms in the next section.
3.2. Mechanisms behind the heat transfer improvement
Here, we analyse the main heat transport mechanisms behind the improved total heat transfer rate due to surface modifications. For that purpose, we quantify the contribution of each heat flux component defined in § 2.2. As discussed in that section, it is convenient to use a periodic computational domain for computing the average heat flux components at statistically steady conditions. We select here ![]() $\mathit {Re}=100$ as our base case operating condition where we are confident about the results using periodic domains (as shown in the previous section) and where we avoid sputtering/entrainment effects. The other base case parameters (Case MP1) are chosen similar to the previous investigations as
$\mathit {Re}=100$ as our base case operating condition where we are confident about the results using periodic domains (as shown in the previous section) and where we avoid sputtering/entrainment effects. The other base case parameters (Case MP1) are chosen similar to the previous investigations as ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\mathit {Pr}_l=10$,
$\mathit {Pr}_l=10$, ![]() $\hat {p}=10\delta _N$ and
$\hat {p}=10\delta _N$ and ![]() $\hat {h}=\hat {l}=\delta _N$, where the laminar film thickness
$\hat {h}=\hat {l}=\delta _N$, where the laminar film thickness ![]() $\delta _N$ is computed at
$\delta _N$ is computed at ![]() $\mathit {Re}=100$ in (2.17). The domain size is
$\mathit {Re}=100$ in (2.17). The domain size is ![]() $L=80\delta _N$ and the grid resolution is here increased to more than
$L=80\delta _N$ and the grid resolution is here increased to more than ![]() $50 \varDelta /\delta _N$ in the film to make sure that all thermal scales are fully resolved and our heat flux computations are accurate.
$50 \varDelta /\delta _N$ in the film to make sure that all thermal scales are fully resolved and our heat flux computations are accurate.
We also perform a simulation on a smooth surface with the same parameters as above in a periodic domain (Case SP1) to compare the heat fluxes through the film with those on modified surfaces. On the smooth surface, a single solitary wave passes through the domain at fully developed conditions. To get a realistic wave-pass frequency, we increase the domain size to ![]() $L=130\delta _N$ that gives the same non-dimensional wave-pass frequency (approximately
$L=130\delta _N$ that gives the same non-dimensional wave-pass frequency (approximately ![]() $f_{wave}(\nu _l/g^2)^{1/3} = 0.036$) as in Case S3 with the inlet–outlet domain on a smooth surface at
$f_{wave}(\nu _l/g^2)^{1/3} = 0.036$) as in Case S3 with the inlet–outlet domain on a smooth surface at ![]() $\mathit {Re}=90$.
$\mathit {Re}=90$.
Our simulations predict ![]() $\mathit {Nu}_{smooth}=0.21$ for the smooth surface (Case SP1) and
$\mathit {Nu}_{smooth}=0.21$ for the smooth surface (Case SP1) and ![]() $\mathit {Nu}_{mod}=0.38$ for the modified surface (Case MP1), showing an increased heat transfer of more than
$\mathit {Nu}_{mod}=0.38$ for the modified surface (Case MP1), showing an increased heat transfer of more than ![]() $80\,\%$. To analyse the reasons for this improvement, we start by qualitatively comparing the instantaneous temperature fields. Figure 9 shows a close-up view of the non-dimensional temperature field in the film on the smooth (figure 9a) and the modified surface (figure 9b). Compared with the smooth surface, we observe relatively thin thermal boundary layers at the wall between the modifications (in fact, somewhat away from them) and on top of them, indicating high wall heat fluxes here. We also observe a boundary layer detachment at the top-right of the modifications and, consequently, a recirculation zone downstream. The hydrodynamic fluctuations in the interface region (region shown schematically in figure 2) seem to induce thermal mixing. This mixing brings relatively hot fluid towards the interface, consequently increasing the local evaporation rate. The mixing also brings relatively cool fluid towards the wall between the modifications, increasing the wall heat transfer here. Certain surface waves also cause detachment of hot fluid in the recirculation zone, transporting more heat towards the interface region.
$80\,\%$. To analyse the reasons for this improvement, we start by qualitatively comparing the instantaneous temperature fields. Figure 9 shows a close-up view of the non-dimensional temperature field in the film on the smooth (figure 9a) and the modified surface (figure 9b). Compared with the smooth surface, we observe relatively thin thermal boundary layers at the wall between the modifications (in fact, somewhat away from them) and on top of them, indicating high wall heat fluxes here. We also observe a boundary layer detachment at the top-right of the modifications and, consequently, a recirculation zone downstream. The hydrodynamic fluctuations in the interface region (region shown schematically in figure 2) seem to induce thermal mixing. This mixing brings relatively hot fluid towards the interface, consequently increasing the local evaporation rate. The mixing also brings relatively cool fluid towards the wall between the modifications, increasing the wall heat transfer here. Certain surface waves also cause detachment of hot fluid in the recirculation zone, transporting more heat towards the interface region.

Figure 9. Instantaneous non-dimensional temperature field in the evaporating falling film (![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\mathit {Pr}_l=10$) on (a) a smooth surface with a solitary wave (Case SP1) and (b) a modified surface (the base case (MP1) with
$\mathit {Pr}_l=10$) on (a) a smooth surface with a solitary wave (Case SP1) and (b) a modified surface (the base case (MP1) with ![]() $\hat {p}=10\delta _N$ and
$\hat {p}=10\delta _N$ and ![]() $\hat {h}=\hat {l}=\delta _N$). The liquid is below the gas–liquid interface (thick grey line) and flows from left to right. The horizontal axes are not scaled in (a) or (b).
$\hat {h}=\hat {l}=\delta _N$). The liquid is below the gas–liquid interface (thick grey line) and flows from left to right. The horizontal axes are not scaled in (a) or (b).
To quantify how the observed qualitative differences influence the heat fluxes through the film, we compute the average heat flux components at statistically steady conditions in the wall-normal direction (fluxes averaged in time and streamwise direction). The liquid heat flux contributions and the average heat flux absorbed by evaporation in the smooth surface case are shown in figure 10(a). Here, it is clear that the dominating mode of heat transport is the mean diffusive flux ![]() $\langle {q} \rangle ^y_{l,{diff}}$. The solitary wave induces some fluctuating advective
$\langle {q} \rangle ^y_{l,{diff}}$. The solitary wave induces some fluctuating advective ![]() $\langle {q'} \rangle ^y_{l,{adv}}$ and diffusive
$\langle {q'} \rangle ^y_{l,{adv}}$ and diffusive ![]() $\langle {q'} \rangle ^y_{l,{diff}}$ fluxes around
$\langle {q'} \rangle ^y_{l,{diff}}$ fluxes around ![]() $x = \delta _N$ which is approximately the average film thickness. Yet, without any surface modifications, the average wall-normal velocity is uniformly zero
$x = \delta _N$ which is approximately the average film thickness. Yet, without any surface modifications, the average wall-normal velocity is uniformly zero ![]() $(\langle {u}_l \rangle (\boldsymbol {x})=0)$, which gives the mean advective flux
$(\langle {u}_l \rangle (\boldsymbol {x})=0)$, which gives the mean advective flux ![]() $\langle {q} \rangle ^y_{l,{adv}}(x)=0$.
$\langle {q} \rangle ^y_{l,{adv}}(x)=0$.

Figure 10. Streamwise averaged wall-normal heat flux components through the film with the parameters ![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\mathit {Pr}_l=10$. The fluxes are normalised by
$\mathit {Pr}_l=10$. The fluxes are normalised by ![]() $\bar {q}_{{evap},{smooth}} = \int _0^L \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}$ that is the average total evaporative heat flux on the smooth surface. Here (a) smooth surface (Case SP1); (b) modified surface (Case MP1).
$\bar {q}_{{evap},{smooth}} = \int _0^L \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}$ that is the average total evaporative heat flux on the smooth surface. Here (a) smooth surface (Case SP1); (b) modified surface (Case MP1).
The streamwise averaged heat fluxes in the case with surface modifications are shown in figure 10(b). Here, the heat fluxes are clearly higher than those for the smooth surface case and the mode of heat transport is significantly altered. The majority of the liquid heat has been absorbed by evaporation at approximately ![]() $x =2\delta _N$ (
$x =2\delta _N$ (![]() $\langle {q} \rangle ^y_{evap}(x)$ is at
$\langle {q} \rangle ^y_{evap}(x)$ is at ![]() $90\,\%$ of its maximum), while this occurs at approximately
$90\,\%$ of its maximum), while this occurs at approximately ![]() $x =\delta _N$ on the smooth surface showing that the heat is transported a longer wall-normal distance with the modifications. On the other hand, evaporation starts already at
$x =\delta _N$ on the smooth surface showing that the heat is transported a longer wall-normal distance with the modifications. On the other hand, evaporation starts already at ![]() $x = 0.2\delta _N$ with the modifications compared with approximately
$x = 0.2\delta _N$ with the modifications compared with approximately ![]() $x = 0.5\delta _N$ on the smooth surface indicating part of the heat is transported a shorter distance.
$x = 0.5\delta _N$ on the smooth surface indicating part of the heat is transported a shorter distance.
Close to the wall, ![]() $x\to 0$, liquid fluctuations diminish and the mean diffusive flux dominates for both cases. However, on the modified surface, the advective contributions (shown in figure 10b) start dominating the total heat flux at approximately
$x\to 0$, liquid fluctuations diminish and the mean diffusive flux dominates for both cases. However, on the modified surface, the advective contributions (shown in figure 10b) start dominating the total heat flux at approximately ![]() $x = 0.2\delta _N$ showing that the surface modifications trigger significant mixing in the majority of the film. The mean advective flux
$x = 0.2\delta _N$ showing that the surface modifications trigger significant mixing in the majority of the film. The mean advective flux ![]() $\langle {q} \rangle ^y_{l,{adv}}$ is positive and greater in magnitude than the fluctuating advective component. The latter component has, however, a maximum magnitude farther out from the wall compared with the former component. This indicates the presence of strong fluctuations in the interface region and high mean advection in the bulk of the film.
$\langle {q} \rangle ^y_{l,{adv}}$ is positive and greater in magnitude than the fluctuating advective component. The latter component has, however, a maximum magnitude farther out from the wall compared with the former component. This indicates the presence of strong fluctuations in the interface region and high mean advection in the bulk of the film.
To further analyse the film heat fluxes, it is useful to study the spatial variation of the wall-normal heat flux contributions prior to the streamwise averaging. Figure 11 shows these contributions in the liquid film on the modified surface. The white and black thick lines represent the surface modifications and the isoline ![]() $\langle H \rangle (\boldsymbol {x}) = 0.5$ that is the average position of the gas–liquid interface. Figure 11(a) shows the mean diffusive flux that is high at the top of the modifications and at the wall between them due to the thin thermal boundary layers found here. Just upstream and downstream of the modifications, the flow is more stagnant and the thermal boundary layer is thicker resulting in a lower diffusive flux. Figure 11(b) shows the fluctuating diffusive flux that is mainly positive and non-zero close to the interface region. This is reasonable since strong temperature fluctuations are typically induced by interfacial waves, while, closer to the wall, the fluctuations are damped.
$\langle H \rangle (\boldsymbol {x}) = 0.5$ that is the average position of the gas–liquid interface. Figure 11(a) shows the mean diffusive flux that is high at the top of the modifications and at the wall between them due to the thin thermal boundary layers found here. Just upstream and downstream of the modifications, the flow is more stagnant and the thermal boundary layer is thicker resulting in a lower diffusive flux. Figure 11(b) shows the fluctuating diffusive flux that is mainly positive and non-zero close to the interface region. This is reasonable since strong temperature fluctuations are typically induced by interfacial waves, while, closer to the wall, the fluctuations are damped.

Figure 11. Average wall-normal heat flux contributions in the evaporative falling film on a modified surface (Case MP1 with ![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\mathit {Pr}_l=10$,
$\mathit {Pr}_l=10$, ![]() $\hat {p}=10\delta _N$ and
$\hat {p}=10\delta _N$ and ![]() $\hat {h}=\hat {l}=\delta _N$). The fluxes are normalised by
$\hat {h}=\hat {l}=\delta _N$). The fluxes are normalised by ![]() $\bar {q}_{evap} = \int _0^L \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}$ that is the average total evaporative heat flux on the modified surface. White and black thick continuous lines represent the surface modifications and the isoline
$\bar {q}_{evap} = \int _0^L \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}$ that is the average total evaporative heat flux on the modified surface. White and black thick continuous lines represent the surface modifications and the isoline ![]() $\langle H \rangle (\boldsymbol {x}) = 0.5$ that is the average position of the gas–liquid interface. Thin black lines are streamlines of the average velocity field. (a) Mean diffusive flux
$\langle H \rangle (\boldsymbol {x}) = 0.5$ that is the average position of the gas–liquid interface. Thin black lines are streamlines of the average velocity field. (a) Mean diffusive flux ![]() $\langle {q} \rangle ^y_{l,{diff}}$. (b) Fluctuating diffusive flux
$\langle {q} \rangle ^y_{l,{diff}}$. (b) Fluctuating diffusive flux ![]() $\langle {q'} \rangle ^y_{l,{diff}}$. (c) Mean advective flux
$\langle {q'} \rangle ^y_{l,{diff}}$. (c) Mean advective flux ![]() $\langle {q} \rangle ^y_{l,{adv}}$. (d) Fluctuating advective flux
$\langle {q} \rangle ^y_{l,{adv}}$. (d) Fluctuating advective flux ![]() $\langle {q'} \rangle ^y_{l,{adv}}$.
$\langle {q'} \rangle ^y_{l,{adv}}$.
Figure 11(c) shows the mean advective flux that is, locally, an order of magnitude larger than the diffusive fluxes. These high values are mainly caused by the relatively high wall-normal velocities induced by the modifications. The maximum and minimum wall-normal locations are roughly at ![]() $x=\delta _N$ and this is also where we observe the maximum
$x=\delta _N$ and this is also where we observe the maximum ![]() $\langle {q} \rangle ^y_{l,{adv}}(x)$ in figure 10(b). In that figure, we also observe significant
$\langle {q} \rangle ^y_{l,{adv}}(x)$ in figure 10(b). In that figure, we also observe significant ![]() $\langle {q} \rangle ^y_{l,{adv}}(x)$ closer to the wall. In this region, the high advective flux is, in contrast, mainly due to the recirculation zone downstream of the modifications that gives a net positive heat transport from the hot wall towards the cooler flow above (see figure 11c).
$\langle {q} \rangle ^y_{l,{adv}}(x)$ closer to the wall. In this region, the high advective flux is, in contrast, mainly due to the recirculation zone downstream of the modifications that gives a net positive heat transport from the hot wall towards the cooler flow above (see figure 11c).
Finally, figure 11(d) shows the fluctuating advective flux with maximum and minimum locations located farther out from the wall compared with the mean advective flux. This is again because of surface waves inducing the strongest fluctuations. Upstream and above the modifications, the fluctuations cause a positive heat flux because of waves being directed out by the modifications. Conversely, downstream, the waves flow towards the wall inducing high negative fluctuations. These features explain the negative values and minimum location of the fluctuating advective heat flux profile in figure 10(b). Still, the fluctuating advective flux is positive and significant in the free stream close to the wall ![]() $0< x<0.5\delta _N$ between the modifications. This stems from the fluctuations generated at the top of the modifications (seen in figure 11d) that are then transported with the free stream towards the wall, thus increasing the mixing here.
$0< x<0.5\delta _N$ between the modifications. This stems from the fluctuations generated at the top of the modifications (seen in figure 11d) that are then transported with the free stream towards the wall, thus increasing the mixing here.
Based on these findings, we propose the following hypothesis of the existence of a sequence of synergistic mechanisms behind the heat transfer improvement by surface modifications. These mechanisms are: (i) relatively well mixed (fluctuating) and cool liquid from the interface region flows along the wall between the modifications and is heated by high diffusive fluxes; (ii) upstream of the modification, the heated fluid is directed outwards, around the modification; (iii) downstream, relatively hot fluid also flows outwards due to the presence of a recirculation zone; (iv) the hot fluid flowing outward mixes with the colder fluid in the interface region due to the strong hydrodynamic fluctuations in the latter region. The four synergistic mechanisms give a well-mixed and relatively hot interface region that induces a higher average evaporation rate to maintain the interface at saturation conditions. The rate of heat transport through the film is, therefore, enhanced compared with the smooth surface.
The mechanisms in the proposed hypothesis are clearly dependent on the governing parameters and operating conditions. For example, by changing the ![]() $\mathit {Re}$ number, we expect different hydrodynamics where the fluctuations of mechanism 4 and the size of the recirculation zone in mechanism 3 change. The length of the recirculation zone behind a bump in single-phase channel flows was studied by Griffith et al. (Reference Griffith, Thompson, Leweke, Hourigan and Anderson2007). By approximating their channel height as our film height, the recirculation length
$\mathit {Re}$ number, we expect different hydrodynamics where the fluctuations of mechanism 4 and the size of the recirculation zone in mechanism 3 change. The length of the recirculation zone behind a bump in single-phase channel flows was studied by Griffith et al. (Reference Griffith, Thompson, Leweke, Hourigan and Anderson2007). By approximating their channel height as our film height, the recirculation length ![]() $L_r/\hat {h}$ should scale roughly as
$L_r/\hat {h}$ should scale roughly as ![]() $\propto \sqrt {Re}$ in the corresponding range of
$\propto \sqrt {Re}$ in the corresponding range of ![]() $\mathit {Re}$ numbers considered in the present study. In the channel flow,
$\mathit {Re}$ numbers considered in the present study. In the channel flow, ![]() $L_r/\hat {h} \approx 5$ for our corresponding
$L_r/\hat {h} \approx 5$ for our corresponding ![]() $\mathit {Re}$ number, while we observe approximately
$\mathit {Re}$ number, while we observe approximately ![]() $L_r/\hat {h} = 3.7$ indicating similar hydrodynamics. The recirculation length scaling suggests that the heat transfer contribution due to the recirculation (mechanism 3) should diminish at lower wetting rates but increase somewhat at higher rates. Contrarily, lower (higher)
$L_r/\hat {h} = 3.7$ indicating similar hydrodynamics. The recirculation length scaling suggests that the heat transfer contribution due to the recirculation (mechanism 3) should diminish at lower wetting rates but increase somewhat at higher rates. Contrarily, lower (higher) ![]() $\mathit {Re}$ give relatively thin (thick) films and thereby higher (lower) diffusive heat fluxes because of the higher (lower) average temperature gradient. Such opposing effects of
$\mathit {Re}$ give relatively thin (thick) films and thereby higher (lower) diffusive heat fluxes because of the higher (lower) average temperature gradient. Such opposing effects of ![]() $\mathit {Re}$ on
$\mathit {Re}$ on ![]() $\mathit {Nu}$ may explain the relatively low influence of
$\mathit {Nu}$ may explain the relatively low influence of ![]() $\mathit {Re}$ on
$\mathit {Re}$ on ![]() $\mathit {Nu}_{mod}$ seen in figure 7.
$\mathit {Nu}_{mod}$ seen in figure 7.
Next, we also analyse the influence of important surface topology and material parameters on the heat transport.
3.3. Influence of surface topology and material parameters on total heat transfer rate
In this section we investigate the influence of the surface modification pitch ![]() $\hat {p}$, height
$\hat {p}$, height ![]() $\hat {h}$ and the liquid Prandtl number
$\hat {h}$ and the liquid Prandtl number ![]() $\mathit {Pr}_l$ on the heat transfer rate through the evaporative film. We use the same simulation set-up and parameters as in the base case of the previous section on the modified surface (
$\mathit {Pr}_l$ on the heat transfer rate through the evaporative film. We use the same simulation set-up and parameters as in the base case of the previous section on the modified surface (![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\mathit {Pr}_l=10$,
$\mathit {Pr}_l=10$, ![]() $\hat {p}=10\delta _N$ and
$\hat {p}=10\delta _N$ and ![]() $\hat {h}=\hat {l}=\delta _N$). Then, we assess the effect of varying
$\hat {h}=\hat {l}=\delta _N$). Then, we assess the effect of varying ![]() $\hat {p}$,
$\hat {p}$, ![]() $\hat {h}$ or
$\hat {h}$ or ![]() $\mathit {Pr}_l$ on the heat transfer rate independently.
$\mathit {Pr}_l$ on the heat transfer rate independently.
3.3.1. Effect of modification pitch distance  $\hat {p}$ on the heat transfer rate
$\hat {p}$ on the heat transfer rate
We simulate ![]() $\hat {p}/\delta _N = (2.5, 5, 10, 20, 40)$ while keeping all other parameters constant. The predicted
$\hat {p}/\delta _N = (2.5, 5, 10, 20, 40)$ while keeping all other parameters constant. The predicted ![]() $\mathit {Nu}$ numbers are shown in figure 12 where we observe a maximum at
$\mathit {Nu}$ numbers are shown in figure 12 where we observe a maximum at ![]() $\hat {p}/\delta _N = 10$ corresponding to the base case. The trend of decreasing
$\hat {p}/\delta _N = 10$ corresponding to the base case. The trend of decreasing ![]() $\mathit {Nu}$ at low or high
$\mathit {Nu}$ at low or high ![]() $\hat {p}$ is reasonable since, in the limit of
$\hat {p}$ is reasonable since, in the limit of ![]() $\hat {p} \to 0$ or
$\hat {p} \to 0$ or ![]() $\hat {p} \to \infty$, the surface topology approaches that of a smooth surface and thus
$\hat {p} \to \infty$, the surface topology approaches that of a smooth surface and thus ![]() $\mathit {Nu}_{mod} \to \mathit {Nu}_{smooth}$. The grey line in figure 12 represents the effect of changing the heat transfer area with
$\mathit {Nu}_{mod} \to \mathit {Nu}_{smooth}$. The grey line in figure 12 represents the effect of changing the heat transfer area with ![]() $\hat {p}$ and is computed as
$\hat {p}$ and is computed as ![]() $\mathit {Nu}_{smooth} A_{{wall,mod}}/A_{{wall,smooth}} = \mathit {Nu}_{smooth}(1+[\hat {l}({\rm \pi} /2-2)+2\hat {h}]/\hat {p})$. Clearly, the trend of the predicted
$\mathit {Nu}_{smooth} A_{{wall,mod}}/A_{{wall,smooth}} = \mathit {Nu}_{smooth}(1+[\hat {l}({\rm \pi} /2-2)+2\hat {h}]/\hat {p})$. Clearly, the trend of the predicted ![]() $\mathit {Nu}_{mod}$ numbers is governed by mechanisms other than just the change of heat transfer area.
$\mathit {Nu}_{mod}$ numbers is governed by mechanisms other than just the change of heat transfer area.

Figure 12. Predicted average heat transfer rate ![]() $\mathit {Nu}$ for an evaporative falling film on a modified surface with varying pitch
$\mathit {Nu}$ for an evaporative falling film on a modified surface with varying pitch ![]() $\hat{p}$ (Cases MP1–5). The governing parameters are
$\hat{p}$ (Cases MP1–5). The governing parameters are ![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\mathit {Pr}_l=10$ and
$\mathit {Pr}_l=10$ and ![]() $\hat {h}=\hat {l}=\delta _N$.
$\hat {h}=\hat {l}=\delta _N$.
To understand why ![]() $\hat {p}/\delta _N = 10$ maximises
$\hat {p}/\delta _N = 10$ maximises ![]() $\mathit {Nu}(\,\hat {p})$, we analyse how the average wall-normal heat fluxes vary with
$\mathit {Nu}(\,\hat {p})$, we analyse how the average wall-normal heat fluxes vary with ![]() $\hat {p}$. These fluxes are shown in figure 13, where we observe that, in figure 13(a), the advective fluxes are the highest for
$\hat {p}$. These fluxes are shown in figure 13, where we observe that, in figure 13(a), the advective fluxes are the highest for ![]() $\hat {p}/\delta _N = 10$. This is mainly because of the length scale of the region with high advection induced upstream and downstream the modification (mechanism 2 and 3). As discussed in § 3.2, the downstream recirculation zone is approximately
$\hat {p}/\delta _N = 10$. This is mainly because of the length scale of the region with high advection induced upstream and downstream the modification (mechanism 2 and 3). As discussed in § 3.2, the downstream recirculation zone is approximately ![]() $L_r/\hat {h} = L_r/\delta _N \approx 4$ (for the present
$L_r/\hat {h} = L_r/\delta _N \approx 4$ (for the present ![]() $\mathit {Re}=100$ and
$\mathit {Re}=100$ and ![]() $\hat {h}=\delta _N$). By assuming a similar length scale for the upstream high advection zone of mechanism 2 (seen in figure 11), the total length of the region with high advection around the modification is close to
$\hat {h}=\delta _N$). By assuming a similar length scale for the upstream high advection zone of mechanism 2 (seen in figure 11), the total length of the region with high advection around the modification is close to ![]() $10\delta _N$ that equals the predicted optimal pitch. Therefore, by increasing
$10\delta _N$ that equals the predicted optimal pitch. Therefore, by increasing ![]() $\hat {p}$ above this value, a region with lower mixing appears between the modifications (lower local advection). This effect decreases the contributions by mechanism 2 and 3 as the streamwise average advective flux decreases. Conversely, by decreasing
$\hat {p}$ above this value, a region with lower mixing appears between the modifications (lower local advection). This effect decreases the contributions by mechanism 2 and 3 as the streamwise average advective flux decreases. Conversely, by decreasing ![]() $\hat {p}$ below
$\hat {p}$ below ![]() $2L_r$ (as in the cases with
$2L_r$ (as in the cases with ![]() $\hat {p}/\delta _N = 5$ and
$\hat {p}/\delta _N = 5$ and ![]() $2.5$) one limits the mixing mechanism 2 and 3 upstream and downstream of the modification and causes recirculation in the entire region between the modifications. Here, we observe in the simulations that the flow detaches from the wall and the bulk of the film flows outside of the modifications. This effect decreases the contributions of mechanisms 1, 2 and 3 close to the wall and gives a maximum of advective fluxes farther out, at approximately
$2.5$) one limits the mixing mechanism 2 and 3 upstream and downstream of the modification and causes recirculation in the entire region between the modifications. Here, we observe in the simulations that the flow detaches from the wall and the bulk of the film flows outside of the modifications. This effect decreases the contributions of mechanisms 1, 2 and 3 close to the wall and gives a maximum of advective fluxes farther out, at approximately ![]() $x=0.8\delta _N$ in figure 13(a) for the cases of
$x=0.8\delta _N$ in figure 13(a) for the cases of ![]() $\hat {p}/\delta _N = 5$ and
$\hat {p}/\delta _N = 5$ and ![]() $2.5$. In summary,
$2.5$. In summary, ![]() $\hat {p}/\delta _N = 10$ gives the highest advective fluxes because
$\hat {p}/\delta _N = 10$ gives the highest advective fluxes because ![]() $\hat {p}$ matches the length scale of the well-mixed (high advective flux) zone induced by the surface modifications (mechanism 2 and 3), while allowing the flow to reattach to the wall between the modifications (mechanism 1).
$\hat {p}$ matches the length scale of the well-mixed (high advective flux) zone induced by the surface modifications (mechanism 2 and 3), while allowing the flow to reattach to the wall between the modifications (mechanism 1).

Figure 13. Average wall-normal advective and diffusive heat flux components through the film for Cases MP1–5 with the parameters ![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\mathit {Pr}_l=10$,
$\mathit {Pr}_l=10$, ![]() $\hat {h}=\hat {l}=\delta _N$ at varying pitch
$\hat {h}=\hat {l}=\delta _N$ at varying pitch ![]() $\hat {p}$. The fluxes are normalised by
$\hat {p}$. The fluxes are normalised by ![]() $\bar {q}_{{evap},{smooth}} = \int _0^L \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}$ that is the average total evaporative heat flux on the smooth surface (Case SP1). (a) Total advective heat flux
$\bar {q}_{{evap},{smooth}} = \int _0^L \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}$ that is the average total evaporative heat flux on the smooth surface (Case SP1). (a) Total advective heat flux ![]() $\langle {q} \rangle ^y_{l,{adv}}+\langle {q'} \rangle ^y_{l,{adv}}$. (b) Total diffusive heat flux
$\langle {q} \rangle ^y_{l,{adv}}+\langle {q'} \rangle ^y_{l,{adv}}$. (b) Total diffusive heat flux ![]() $\langle {q} \rangle ^y_{l,{diff}}+\langle {q'} \rangle ^y_{l,{diff}}$.
$\langle {q} \rangle ^y_{l,{diff}}+\langle {q'} \rangle ^y_{l,{diff}}$.
Yet, the diffusive fluxes for ![]() $\hat {p}/\delta _N = 2.5$ and
$\hat {p}/\delta _N = 2.5$ and ![]() $5$ are high at the top of the modifications
$5$ are high at the top of the modifications ![]() $x=\delta _N$, indicating that a significant part of the total wall heat flux now comes from the modification surfaces and not the wall in between. That these fluxes are high in the region
$x=\delta _N$, indicating that a significant part of the total wall heat flux now comes from the modification surfaces and not the wall in between. That these fluxes are high in the region ![]() $\delta _N < x < 2\delta _N$ further confirms that the hydrodynamics and governing heat transfer mechanisms are different from those at
$\delta _N < x < 2\delta _N$ further confirms that the hydrodynamics and governing heat transfer mechanisms are different from those at ![]() $\hat {p}/\delta _N \geq 10$. The diffusive fluxes for
$\hat {p}/\delta _N \geq 10$. The diffusive fluxes for ![]() $\hat {p}/\delta _N = 10$ are also relatively high around the top of the modifications
$\hat {p}/\delta _N = 10$ are also relatively high around the top of the modifications ![]() $x=\delta _N$, indicating the extra heat transfer due to a larger heat transfer area is still significant at this pitch.
$x=\delta _N$, indicating the extra heat transfer due to a larger heat transfer area is still significant at this pitch.
The advective and diffusive heat fluxes thus indicate ![]() $\hat {p}/\delta _N = 10$ is a good compromise between increasing the heat transfer area while maintaining the attached flow (enabling mechanism 1) and inducing high mixing around the modifications (mechanism 2 and 3).
$\hat {p}/\delta _N = 10$ is a good compromise between increasing the heat transfer area while maintaining the attached flow (enabling mechanism 1) and inducing high mixing around the modifications (mechanism 2 and 3).
Next, we analyse the effect of the modification height ![]() $\hat {h}$ on
$\hat {h}$ on ![]() $\mathit {Nu}$.
$\mathit {Nu}$.
3.3.2. Effect of modification height  $\hat {h}$ on the heat transfer
$\hat {h}$ on the heat transfer
Here, we assess the influence of ![]() $\hat {h}/\delta _N = (0.5, 1, 2, 4)$ on
$\hat {h}/\delta _N = (0.5, 1, 2, 4)$ on ![]() $\mathit {Nu}_{mod}$ while keeping the other parameters constant. The results are shown in figure 14 that show monotonically increasing
$\mathit {Nu}_{mod}$ while keeping the other parameters constant. The results are shown in figure 14 that show monotonically increasing ![]() $\mathit {Nu}_{mod}(\hat {h})$ with an approximate scaling of
$\mathit {Nu}_{mod}(\hat {h})$ with an approximate scaling of ![]() $\mathit {Nu}_{mod} \propto \hat {h}^{0.27}$. The results indicate
$\mathit {Nu}_{mod} \propto \hat {h}^{0.27}$. The results indicate ![]() $\mathit {Nu}_{mod} \to \mathit {Nu}_{smooth}$ as
$\mathit {Nu}_{mod} \to \mathit {Nu}_{smooth}$ as ![]() $\hat {h} \to 0$ which is reasonable since the surface topology then approaches that of a smooth surface. At the largest
$\hat {h} \to 0$ which is reasonable since the surface topology then approaches that of a smooth surface. At the largest ![]() $\hat {h}/\delta _N = 4$, we observe significant sputtering events and
$\hat {h}/\delta _N = 4$, we observe significant sputtering events and ![]() $\mathit {Nu}_{mod}$ here is therefore not certain although it follows the approximate scaling and thus seems plausible. Other statistics such as the average fluxes are, however, not converged for
$\mathit {Nu}_{mod}$ here is therefore not certain although it follows the approximate scaling and thus seems plausible. Other statistics such as the average fluxes are, however, not converged for ![]() $\hat {h}=4\delta _N$ and are therefore not included in the subsequent analysis.
$\hat {h}=4\delta _N$ and are therefore not included in the subsequent analysis.

Figure 14. Predicted average heat transfer rate ![]() $\mathit {Nu}$ for an evaporative falling film on a modified surface with varying modification height
$\mathit {Nu}$ for an evaporative falling film on a modified surface with varying modification height ![]() $\hat {h}$ (Cases MP1, 6, 7, 8). The governing parameters are
$\hat {h}$ (Cases MP1, 6, 7, 8). The governing parameters are ![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\mathit {Pr}_l=10$,
$\mathit {Pr}_l=10$, ![]() $\hat {p}=10\delta _N$ and
$\hat {p}=10\delta _N$ and ![]() $\hat {l}=\delta _N$.
$\hat {l}=\delta _N$.
The grey line in figure 14 represents the effect of increasing heat transfer area with ![]() $\hat {h}$ (defined in the previous section) and shows a similar scaling as
$\hat {h}$ (defined in the previous section) and shows a similar scaling as ![]() $\mathit {Nu}_{mod}(\hat {h})$ in the present range of parameters. It is therefore probable that the larger heat transfer area can partly explain the increase of
$\mathit {Nu}_{mod}(\hat {h})$ in the present range of parameters. It is therefore probable that the larger heat transfer area can partly explain the increase of ![]() $\mathit {Nu}_{mod}$ with
$\mathit {Nu}_{mod}$ with ![]() $\hat {h}$. This observation will be further assessed below.
$\hat {h}$. This observation will be further assessed below.
To understand why the heat transfer rate increases with ![]() $\hat {h}$, we analyse how the average wall-normal advective and diffusive heat fluxes vary with
$\hat {h}$, we analyse how the average wall-normal advective and diffusive heat fluxes vary with ![]() $\hat {h}$ in figure 15 (note that
$\hat {h}$ in figure 15 (note that ![]() $x$ is scaled by
$x$ is scaled by ![]() $\hat {h}$ so that
$\hat {h}$ so that ![]() $x/\hat {h}=1$ is the top of the modifications for all the cases). In figure 15(a), the advective fluxes are almost doubled from the case
$x/\hat {h}=1$ is the top of the modifications for all the cases). In figure 15(a), the advective fluxes are almost doubled from the case ![]() $\hat {h}/\delta _N=0.5$ to
$\hat {h}/\delta _N=0.5$ to ![]() $1$ indicating that the improvement of
$1$ indicating that the improvement of ![]() $\mathit {Nu}_{mod}$ between these cases is due to a better mixing (mechanisms 1–4) rather than an increased surface area.
$\mathit {Nu}_{mod}$ between these cases is due to a better mixing (mechanisms 1–4) rather than an increased surface area.

Figure 15. Average wall-normal heat flux components through the film for Cases MP1, 6, 7 and 8 with the parameters ![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\mathit {Pr}_l=10$,
$\mathit {Pr}_l=10$, ![]() $\hat {l}=\delta _N$ and
$\hat {l}=\delta _N$ and ![]() $\hat {p}=10\delta _N$ at varying height
$\hat {p}=10\delta _N$ at varying height ![]() $\hat {h}$. All fluxes are normalised by
$\hat {h}$. All fluxes are normalised by ![]() $\bar {q}_{{evap},{smooth}} = \int _0^L \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}$ that is the average total evaporative heat flux on the smooth surface (Case SP1). The fluxes on the smooth surface are shown for comparison and here
$\bar {q}_{{evap},{smooth}} = \int _0^L \langle q_{{evap},S} \rangle ^y \,{{\rm d}{\kern0.8pt}x}$ that is the average total evaporative heat flux on the smooth surface (Case SP1). The fluxes on the smooth surface are shown for comparison and here ![]() $x$ is normalised by
$x$ is normalised by ![]() $\delta _N$. (a) Total advective heat flux
$\delta _N$. (a) Total advective heat flux ![]() $\langle {q} \rangle ^y_{l,{adv}}+\langle {q'} \rangle ^y_{l,{adv}}$. (b) Solid lines are the total diffusive heat flux
$\langle {q} \rangle ^y_{l,{adv}}+\langle {q'} \rangle ^y_{l,{adv}}$. (b) Solid lines are the total diffusive heat flux ![]() $\langle {q} \rangle ^y_{l,{diff}}+\langle {q'} \rangle ^y_{l,{diff}}$ and dotted lines are
$\langle {q} \rangle ^y_{l,{diff}}+\langle {q'} \rangle ^y_{l,{diff}}$ and dotted lines are ![]() $\langle {q} \rangle ^y_{evap}$ that represent the cumulative heat flux absorbed by evaporation up to location
$\langle {q} \rangle ^y_{evap}$ that represent the cumulative heat flux absorbed by evaporation up to location ![]() $x$.
$x$.
For the cases with ![]() $\hat {h}/\delta _N=1$ and
$\hat {h}/\delta _N=1$ and ![]() $2$, the advective fluxes are similar in the region of
$2$, the advective fluxes are similar in the region of ![]() $0< x<0.6\hat {h}$ (flow between modifications) showing that the mixing is not significantly improved here by increasing
$0< x<0.6\hat {h}$ (flow between modifications) showing that the mixing is not significantly improved here by increasing ![]() $\hat {h}$. This is again related to the length of the zone with high advective fluxes (mechanism 2 and 3) discussed in §§ 3.2 and 3.3.1. As shown by Griffith et al. (Reference Griffith, Thompson, Leweke, Hourigan and Anderson2007), the length of the recirculation zone is proportional to the height of the bump. We observe the similar trend in the average velocity field with
$\hat {h}$. This is again related to the length of the zone with high advective fluxes (mechanism 2 and 3) discussed in §§ 3.2 and 3.3.1. As shown by Griffith et al. (Reference Griffith, Thompson, Leweke, Hourigan and Anderson2007), the length of the recirculation zone is proportional to the height of the bump. We observe the similar trend in the average velocity field with ![]() $L_r/\hat {h}=(3.6, 3.7, 3.2)$ for
$L_r/\hat {h}=(3.6, 3.7, 3.2)$ for ![]() $\hat {h}/\delta _N=(0.5, 1, 2)$, respectively, while for
$\hat {h}/\delta _N=(0.5, 1, 2)$, respectively, while for ![]() $\hat {h}/\delta _N=4$, the recirculation zone (with an expected length
$\hat {h}/\delta _N=4$, the recirculation zone (with an expected length ![]() $L_r/\hat {h} \approx 3$ at a free downstream flow) reaches the downstream modification since here
$L_r/\hat {h} \approx 3$ at a free downstream flow) reaches the downstream modification since here ![]() $\hat {p}/\hat {h} = 2.5 < L_r/\hat {h}$. In the latter case, the average flow detaches and recirculates in the entire region between the modifications. On the other hand, in the region
$\hat {p}/\hat {h} = 2.5 < L_r/\hat {h}$. In the latter case, the average flow detaches and recirculates in the entire region between the modifications. On the other hand, in the region ![]() $0.7\hat {h}< x<1.3\hat {h}$ (flow around the top of the modifications), the advective fluxes in figure 15(a) are monotonically increasing with
$0.7\hat {h}< x<1.3\hat {h}$ (flow around the top of the modifications), the advective fluxes in figure 15(a) are monotonically increasing with ![]() $h$ indicating more intense mixing in the interface region (mechanism 4).
$h$ indicating more intense mixing in the interface region (mechanism 4).
Longer recirculation zones increase the heat transfer through mechanism 3 but also have a shielding effect that reduces the wall heat flux between modifications through mechanism 1. As shown in § 3.3.1, an optimal ![]() $\mathit {Nu}_{mod}(\,\hat {p})$ is achieved at
$\mathit {Nu}_{mod}(\,\hat {p})$ is achieved at ![]() $L_r/\hat {p}\approx 0.4$ indicating this is a good compromise between mechanisms 1 and 3. For the cases here with
$L_r/\hat {p}\approx 0.4$ indicating this is a good compromise between mechanisms 1 and 3. For the cases here with ![]() $\hat {h}/\delta _N=(0.5, 1, 2)$ we get the ratios
$\hat {h}/\delta _N=(0.5, 1, 2)$ we get the ratios ![]() $L_r/\hat {p}=(0.18, 0.37, 0.64)$, respectively. For
$L_r/\hat {p}=(0.18, 0.37, 0.64)$, respectively. For ![]() $\hat {h}/\delta _N=1$ with
$\hat {h}/\delta _N=1$ with ![]() $L_r/\hat {p}\approx 0.4$ we find indeed the highest wall heat flux
$L_r/\hat {p}\approx 0.4$ we find indeed the highest wall heat flux ![]() $\langle {q} \rangle ^y_{wall}(x=0) = \langle {q} \rangle ^y_{l,{diff}}(x=0)$ in figure 15(b), although the differences between the cases are not great. The relatively small differences indicate that the net effect of the mixing mechanisms on
$\langle {q} \rangle ^y_{wall}(x=0) = \langle {q} \rangle ^y_{l,{diff}}(x=0)$ in figure 15(b), although the differences between the cases are not great. The relatively small differences indicate that the net effect of the mixing mechanisms on ![]() $\langle {q} \rangle ^y_{wall}(x=0)$ is nearly constant with
$\langle {q} \rangle ^y_{wall}(x=0)$ is nearly constant with ![]() $\hat {h}$ in the present range of parameters.
$\hat {h}$ in the present range of parameters.
To understand why larger ![]() $\hat {h}$ still improves
$\hat {h}$ still improves ![]() $\mathit {Nu}_{mod}$, we return to the heat flux balance of (2.27). The balance shows that the total heat applied by the entire heated surface (the modification surface and the wall between them) equals the total heat absorbed by evaporation
$\mathit {Nu}_{mod}$, we return to the heat flux balance of (2.27). The balance shows that the total heat applied by the entire heated surface (the modification surface and the wall between them) equals the total heat absorbed by evaporation ![]() $Q_{wall}(x=\infty ) = Q_{evap}(x=\infty )$. We split
$Q_{wall}(x=\infty ) = Q_{evap}(x=\infty )$. We split ![]() $Q_{wall}(x=\infty ) = Q_{wall}(x=0) + Q_{{mod,tot}}$ into separate contributions from the wall between the modifications and the modified surface and note that
$Q_{wall}(x=\infty ) = Q_{wall}(x=0) + Q_{{mod,tot}}$ into separate contributions from the wall between the modifications and the modified surface and note that ![]() $Q_{wall}(x=0) = \langle {q} \rangle ^y_{l,{diff}}(x=0)L_y(x=0)$ and
$Q_{wall}(x=0) = \langle {q} \rangle ^y_{l,{diff}}(x=0)L_y(x=0)$ and ![]() $Q_{evap}(x=\infty ) = \langle {q} \rangle ^y_{evap}(x=\infty )L_y(x=\infty )$. As previously discussed,
$Q_{evap}(x=\infty ) = \langle {q} \rangle ^y_{evap}(x=\infty )L_y(x=\infty )$. As previously discussed, ![]() $Q_{wall}(x=0)$ is nearly constant with
$Q_{wall}(x=0)$ is nearly constant with ![]() $\hat {h}$, so the improvement of
$\hat {h}$, so the improvement of ![]() $\mathit {Nu}_{mod}$ with
$\mathit {Nu}_{mod}$ with ![]() $\hat {h}$ must be mainly due to the contribution by
$\hat {h}$ must be mainly due to the contribution by ![]() $Q_{{mod,tot}}$. The relative contributions
$Q_{{mod,tot}}$. The relative contributions ![]() $Q_{{mod,tot}} / Q_{evap}(x=\infty )$ for the cases
$Q_{{mod,tot}} / Q_{evap}(x=\infty )$ for the cases ![]() $\hat {h}/\delta _N=(0.5, 1, 2)$ are, respectively,
$\hat {h}/\delta _N=(0.5, 1, 2)$ are, respectively, ![]() $(0.16, 0.22, 0.41)$. These values show that the relative contribution by
$(0.16, 0.22, 0.41)$. These values show that the relative contribution by ![]() $Q_{{mod,tot}}$ to
$Q_{{mod,tot}}$ to ![]() $Q_{evap}(x=\infty )$ does not change significantly from
$Q_{evap}(x=\infty )$ does not change significantly from ![]() $\hat {h}/\delta _N=0.5$ to
$\hat {h}/\delta _N=0.5$ to ![]() $1$, while from
$1$, while from ![]() $\hat {h}/\delta _N=1$ to
$\hat {h}/\delta _N=1$ to ![]() $2$ the contribution nearly doubles. This can be explained by the fact that the relative surface area increases (compared with a smooth surface) for the cases
$2$ the contribution nearly doubles. This can be explained by the fact that the relative surface area increases (compared with a smooth surface) for the cases ![]() $\hat {h}/\delta _N=(0.5, 1, 2)$ that are, respectively,
$\hat {h}/\delta _N=(0.5, 1, 2)$ that are, respectively, ![]() $(0.06, 0.16, 0.36)$ showing a similar trend as
$(0.06, 0.16, 0.36)$ showing a similar trend as ![]() $Q_{{mod,tot}} / Q_{evap}(x=\infty )$. Comparing the former and latter ratios also shows that the efficiency (average wall heat flux on the modification surface) decreases with
$Q_{{mod,tot}} / Q_{evap}(x=\infty )$. Comparing the former and latter ratios also shows that the efficiency (average wall heat flux on the modification surface) decreases with ![]() $\hat {h}$.
$\hat {h}$.
The above analysis shows that although larger ![]() $\hat {h}$ improve
$\hat {h}$ improve ![]() $\mathit {Nu}_{mod}$, the improvement for
$\mathit {Nu}_{mod}$, the improvement for ![]() $\hat {h}/\delta _N > 1$ is mainly due to a larger heat transfer surface rather than more efficient mixing. Too large
$\hat {h}/\delta _N > 1$ is mainly due to a larger heat transfer surface rather than more efficient mixing. Too large ![]() $\hat {h}$, may, however, produce unwanted sputtering/entrainment effects or even stagnant liquid at the wall/modification junction. The findings in this study thus suggest the modification height
$\hat {h}$, may, however, produce unwanted sputtering/entrainment effects or even stagnant liquid at the wall/modification junction. The findings in this study thus suggest the modification height ![]() $\hat {h}$ should be maximised just below the occurrence of the latter unwanted phenomena to optimise
$\hat {h}$ should be maximised just below the occurrence of the latter unwanted phenomena to optimise ![]() $\mathit {Nu}_{mod}(\hat {h})$.
$\mathit {Nu}_{mod}(\hat {h})$.
In § 3.3.1, ![]() $\mathit {Nu}_{mod}(\hat {p})$ showed an optimum at
$\mathit {Nu}_{mod}(\hat {p})$ showed an optimum at ![]() $\hat {p}/\delta _N = 10$ with
$\hat {p}/\delta _N = 10$ with ![]() $\hat {h}/\delta _N = 1$ and the subsequent analysis suggested an optimum recirculation length
$\hat {h}/\delta _N = 1$ and the subsequent analysis suggested an optimum recirculation length ![]() $L_r/\hat {p}\approx 0.4$. In the present section, the recirculation length is found to be proportional to
$L_r/\hat {p}\approx 0.4$. In the present section, the recirculation length is found to be proportional to ![]() $\hat {h}$ with
$\hat {h}$ with ![]() $L_r/\hat {h}\approx 3.5$. These relations indicate an optimal height to pitch ratio of
$L_r/\hat {h}\approx 3.5$. These relations indicate an optimal height to pitch ratio of ![]() $\hat {h}/\hat {p} = 0.11$ for the present range of parameters, and, show that
$\hat {h}/\hat {p} = 0.11$ for the present range of parameters, and, show that ![]() $\hat {h}$ and
$\hat {h}$ and ![]() $\hat {p}$ should not be tuned independently to optimise
$\hat {p}$ should not be tuned independently to optimise ![]() $\mathit {Nu}_{mod}(\hat {p},\hat {h})$.
$\mathit {Nu}_{mod}(\hat {p},\hat {h})$.
In the next section, we finalise the parameter study by investigating the effect of the ![]() $\mathit {Pr}_l$ number on the heat transfer.
$\mathit {Pr}_l$ number on the heat transfer.
3.3.3. Effect of the liquid Prandtl number  $\mathit {Pr}_l$ on the heat transfer
$\mathit {Pr}_l$ on the heat transfer
In this section we assess the influence of ![]() $\mathit {Pr}_l = (5, 10, 20)$ on
$\mathit {Pr}_l = (5, 10, 20)$ on ![]() $\mathit {Nu}_{mod}$ (for the base case with modified surface defined in § 3.2) while keeping the other parameters constant. The
$\mathit {Nu}_{mod}$ (for the base case with modified surface defined in § 3.2) while keeping the other parameters constant. The ![]() $\mathit {Pr}_l$ and
$\mathit {Pr}_l$ and ![]() $\mathit {Nu}_{mod}$ are both inversely proportional to the thermal conductivity
$\mathit {Nu}_{mod}$ are both inversely proportional to the thermal conductivity ![]() $k_l$ since the thermal diffusivity reads
$k_l$ since the thermal diffusivity reads ![]() $D_l=k_l/(\rho _l c_{p,l})$. In this study, we assume the non-dimensional specific heat
$D_l=k_l/(\rho _l c_{p,l})$. In this study, we assume the non-dimensional specific heat ![]() $c_{p,l}$ constant and equals unity. With the non-dimensional parameters
$c_{p,l}$ constant and equals unity. With the non-dimensional parameters ![]() $\rho _l=\nu _l=g=1$, we get the relation
$\rho _l=\nu _l=g=1$, we get the relation ![]() $\mathit {Nu}_{mod} = \mathit {Pr}_l h_e$. Although the latter relation suggests
$\mathit {Nu}_{mod} = \mathit {Pr}_l h_e$. Although the latter relation suggests ![]() $\mathit {Nu}_{mod} \propto \mathit {Pr}_l^1$, the heat transfer coefficient
$\mathit {Nu}_{mod} \propto \mathit {Pr}_l^1$, the heat transfer coefficient ![]() $h_e$ decreases with
$h_e$ decreases with ![]() $\mathit {Pr}_l$, resulting in a lower effective scaling. The predicted
$\mathit {Pr}_l$, resulting in a lower effective scaling. The predicted ![]() $\mathit {Nu}_{mod}$ from our simulations are shown in figure 16 and show indeed an effective scaling of
$\mathit {Nu}_{mod}$ from our simulations are shown in figure 16 and show indeed an effective scaling of ![]() $\mathit {Nu}_{mod} \propto \mathit {Pr}_l^{0.42}$ in the present range of parameters.
$\mathit {Nu}_{mod} \propto \mathit {Pr}_l^{0.42}$ in the present range of parameters.

Figure 16. Predicted average heat transfer rate ![]() $\mathit {Nu}$ for an evaporative falling film on a modified surface with varying liquid Prandtl number
$\mathit {Nu}$ for an evaporative falling film on a modified surface with varying liquid Prandtl number ![]() $\mathit {Pr}_l$ (Cases MP1, 9, 10). The governing parameters are
$\mathit {Pr}_l$ (Cases MP1, 9, 10). The governing parameters are ![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\hat {p}=10\delta _N$ and
$\hat {p}=10\delta _N$ and ![]() $\hat {h}=\hat {l}=\delta _N$. By definition,
$\hat {h}=\hat {l}=\delta _N$. By definition, ![]() $\mathit {Nu}$ and
$\mathit {Nu}$ and ![]() $\mathit {Pr}_l$ are both proportional to the liquid thermal conductivity which suggests the scaling
$\mathit {Pr}_l$ are both proportional to the liquid thermal conductivity which suggests the scaling ![]() $\mathit {Nu} \propto \mathit {Pr}_l^1$. However,
$\mathit {Nu} \propto \mathit {Pr}_l^1$. However, ![]() $\mathit {Nu}$ is also proportional to the heat transfer coefficient
$\mathit {Nu}$ is also proportional to the heat transfer coefficient ![]() $h_e$ that decreases with
$h_e$ that decreases with ![]() $\mathit {Pr}_l$, resulting in the lower effective scaling.
$\mathit {Pr}_l$, resulting in the lower effective scaling.
Figure 17 shows the average wall-normal advective (figure 17a) and diffusive (figure 17b) fluxes through the film. At the wall ![]() $x=0$, the diffusive heat flux clearly decreases with
$x=0$, the diffusive heat flux clearly decreases with ![]() $\mathit {Pr}_l$ because of the lower relative diffusivity. Consequently, the heat applied by the wall decreases with
$\mathit {Pr}_l$ because of the lower relative diffusivity. Consequently, the heat applied by the wall decreases with ![]() $\mathit {Pr}_l$. This gives a proportional decrease of advective fluxes farther out from the wall (advective maxima at approximately
$\mathit {Pr}_l$. This gives a proportional decrease of advective fluxes farther out from the wall (advective maxima at approximately ![]() $x/\delta _N=0.4$ decrease proportionally to the wall heat flux). Although the magnitude of the advective and diffusive fluxes decreases with
$x/\delta _N=0.4$ decrease proportionally to the wall heat flux). Although the magnitude of the advective and diffusive fluxes decreases with ![]() $\mathit {Pr}_l$, the curves are almost self-similar because the hydrodynamics (governing the shape) is not influenced by
$\mathit {Pr}_l$, the curves are almost self-similar because the hydrodynamics (governing the shape) is not influenced by ![]() $\mathit {Pr}_l$ but the total heat transfer through the film is limited by diffusion at the wall (magnitude governed by
$\mathit {Pr}_l$ but the total heat transfer through the film is limited by diffusion at the wall (magnitude governed by ![]() $\mathit {Pr}_l$).
$\mathit {Pr}_l$).

Figure 17. Average wall-normal heat flux components through the film for the Cases MP1, 9 and 10 with the parameters ![]() $\mathit {Re}=100$,
$\mathit {Re}=100$, ![]() $\mathit {Ka}=488$,
$\mathit {Ka}=488$, ![]() $\hat {p}=10\delta _N$ and
$\hat {p}=10\delta _N$ and ![]() $\hat {h}=\hat {l}=\delta _N$ at varying height
$\hat {h}=\hat {l}=\delta _N$ at varying height ![]() $\mathit {Pr}_l$. All fluxes are normalised by
$\mathit {Pr}_l$. All fluxes are normalised by ![]() $\bar {q}_{{evap},{smooth}} = \int _0^L \langle q_{{evap},S} \rangle ^y {{\rm d}\kern 0.05em x}$ that is the average total evaporative heat flux on the smooth surface with
$\bar {q}_{{evap},{smooth}} = \int _0^L \langle q_{{evap},S} \rangle ^y {{\rm d}\kern 0.05em x}$ that is the average total evaporative heat flux on the smooth surface with ![]() $\mathit {Pr}_l=10$ (Case SP1). (a) Total advective heat flux
$\mathit {Pr}_l=10$ (Case SP1). (a) Total advective heat flux ![]() $\langle {q} \rangle ^y_{l,{adv}}+\langle {q'} \rangle ^y_{l,{adv}}$. (b) Total diffusive heat flux
$\langle {q} \rangle ^y_{l,{adv}}+\langle {q'} \rangle ^y_{l,{adv}}$. (b) Total diffusive heat flux ![]() $\langle {q} \rangle ^y_{l,{diff}}+\langle {q'} \rangle ^y_{l,{diff}}$.
$\langle {q} \rangle ^y_{l,{diff}}+\langle {q'} \rangle ^y_{l,{diff}}$.
The approximate self-similarity shows that the optimal topology parameters for the surface modifications are not significantly dependent on ![]() $\mathit {Pr}_l$ at these relatively high
$\mathit {Pr}_l$ at these relatively high ![]() $\mathit {Pr}_l$ numbers. The topology parameters rather influence the mixing that induces advective heat transfer through mechanisms 1–4. In these cases, the magnitude of the advective heat transfer is clearly limited by diffusion at the wall and not the mixing. However, for more extreme topology parameters the effects of larger heat transfer area may be significant.
$\mathit {Pr}_l$ numbers. The topology parameters rather influence the mixing that induces advective heat transfer through mechanisms 1–4. In these cases, the magnitude of the advective heat transfer is clearly limited by diffusion at the wall and not the mixing. However, for more extreme topology parameters the effects of larger heat transfer area may be significant.
In the next section, we finalise our study by assessing how the relative importance of advective and diffusive heat transfer phenomena influences the overall heat transfer rate ![]() $\mathit {Nu}$.
$\mathit {Nu}$.
3.4. Analysis of governing dimensionless parameters on the overall heat transfer rate
Here, we summarise our results by analysing how key global dimensionless parameters can explain the overall heat transfer rate on both smooth and modified surfaces.
As shown previously, the surface modifications induce significant advective heat transfer (mixing) that typically dominates over the diffusive heat transfer in most of the film. Assuming the advective heat transfer proportional to the standard deviation of the wall-normal liquid velocity ![]() $u_{l,{std}}$, we define the Péclet number
$u_{l,{std}}$, we define the Péclet number ![]() $\mathit {Pe}_l = u_{l,{std}} \delta _N / D_l$ that represents the relative importance of the advective to diffusive heat transport through the film.
$\mathit {Pe}_l = u_{l,{std}} \delta _N / D_l$ that represents the relative importance of the advective to diffusive heat transport through the film.
Based on our previous investigations, we expect the total heat transfer rate to increase with ![]() $u_{l,{std}}$ (
$u_{l,{std}}$ (![]() $\mathit {Nu}$ increases) and, obviously, the diffusive heat transfer rate to increase with
$\mathit {Nu}$ increases) and, obviously, the diffusive heat transfer rate to increase with ![]() $D_l$ (
$D_l$ (![]() $\mathit {Nu}$ decreases by definition with
$\mathit {Nu}$ decreases by definition with ![]() $D_l$). Both of these effects thus give an increase of
$D_l$). Both of these effects thus give an increase of ![]() $\mathit {Nu}$ with
$\mathit {Nu}$ with ![]() $\mathit {Pe}_l$. Figure 18(a) shows
$\mathit {Pe}_l$. Figure 18(a) shows ![]() $\mathit {Nu}$ versus
$\mathit {Nu}$ versus ![]() $\mathit {Pe}_l$ for all our simulation cases in this study. Here, the filled symbols are taken from the investigation in § 3.1 where we varied the
$\mathit {Pe}_l$ for all our simulation cases in this study. Here, the filled symbols are taken from the investigation in § 3.1 where we varied the ![]() $\mathit {Re}$ number on both a smooth surface and a modified surface with constant topology parameters. The empty symbols are values taken from the parameter studies in §§ 3.3.1–3.3.3 where we maintain
$\mathit {Re}$ number on both a smooth surface and a modified surface with constant topology parameters. The empty symbols are values taken from the parameter studies in §§ 3.3.1–3.3.3 where we maintain ![]() $\mathit {Re}=100$ but vary the surface topology and
$\mathit {Re}=100$ but vary the surface topology and ![]() $\mathit {Pr}_l$ parameters. In figure 18(a), we observe indeed an approximate scaling of
$\mathit {Pr}_l$ parameters. In figure 18(a), we observe indeed an approximate scaling of ![]() $\mathit {Nu} \propto \mathit {Pe}_l^{0.3}$ for the cases
$\mathit {Nu} \propto \mathit {Pe}_l^{0.3}$ for the cases ![]() $\mathit {Re}\approx 100$ (blue colour). This indicates that, at a given
$\mathit {Re}\approx 100$ (blue colour). This indicates that, at a given ![]() $\mathit {Re}$ number (and
$\mathit {Re}$ number (and ![]() $\mathit {Pe}_l \gg 1$ where advection dominates), the total heat transfer rate (
$\mathit {Pe}_l \gg 1$ where advection dominates), the total heat transfer rate (![]() $\mathit {Nu}$) correlates with the proposed measure of advective to diffusive heat transport (
$\mathit {Nu}$) correlates with the proposed measure of advective to diffusive heat transport (![]() $\mathit {Pe}_l$) on both smooth and modified surfaces.
$\mathit {Pe}_l$) on both smooth and modified surfaces.

Figure 18. Dependence of global parameters for evaporative falling films on modified and smooth surfaces. The data points are from all our simulation cases in table 1, with circles representing smooth and diamonds modified surfaces. (a) The ![]() $\mathit {Nu}$ versus the liquid Péclet number
$\mathit {Nu}$ versus the liquid Péclet number ![]() $Pe_l$ and colours representing
$Pe_l$ and colours representing ![]() $\mathit {Re}$; (b)
$\mathit {Re}$; (b) ![]() $\mathit {Re}$ versus
$\mathit {Re}$ versus ![]() $Pe_l$ and colours representing
$Pe_l$ and colours representing ![]() $\mathit {Nu}$; (c)
$\mathit {Nu}$; (c) ![]() $\mathit {Nu}$ versus the ratio
$\mathit {Nu}$ versus the ratio ![]() $Pe_l/Re$ indicating the efficiency of the surface topology at generating mixing for a given operating condition and colours representing
$Pe_l/Re$ indicating the efficiency of the surface topology at generating mixing for a given operating condition and colours representing ![]() $\mathit {Re}$.
$\mathit {Re}$.
In figure 18(a) we also observe an ![]() $\mathit {Re}$ number effect in the filled symbols (with fixed surface topology) where higher
$\mathit {Re}$ number effect in the filled symbols (with fixed surface topology) where higher ![]() $\mathit {Re}$ gives higher
$\mathit {Re}$ gives higher ![]() $\mathit {Pe}_l$ but not necessarily higher
$\mathit {Pe}_l$ but not necessarily higher ![]() $\mathit {Nu}$. This can be explained by the fact that the film thickness increases with the flow rate
$\mathit {Nu}$. This can be explained by the fact that the film thickness increases with the flow rate ![]() $\mathit {Re}$ (thermal resistance increases and
$\mathit {Re}$ (thermal resistance increases and ![]() $\mathit {Nu}$ decreases), but, in general, also the mixing increases with
$\mathit {Nu}$ decreases), but, in general, also the mixing increases with ![]() $\mathit {Re}$ (increases
$\mathit {Re}$ (increases ![]() $\mathit {Nu}$). To examine the overall relation between
$\mathit {Nu}$). To examine the overall relation between ![]() $\mathit {Re}$ and
$\mathit {Re}$ and ![]() $\mathit {Pe}_l$, we show in figure 18(b) all the cases from figure 18(a) in the
$\mathit {Pe}_l$, we show in figure 18(b) all the cases from figure 18(a) in the ![]() $\mathit {Re}$–
$\mathit {Re}$–![]() $\mathit {Pe}_l$ plane. Here, we observe the approximate scaling of
$\mathit {Pe}_l$ plane. Here, we observe the approximate scaling of ![]() $\mathit {Re} \propto \mathit {Pe}_l^{1.3}$ for the cases with the same surface topology (filled symbols for both smooth and modified surface), showing that
$\mathit {Re} \propto \mathit {Pe}_l^{1.3}$ for the cases with the same surface topology (filled symbols for both smooth and modified surface), showing that ![]() $\mathit {Re}$ increases mixing (
$\mathit {Re}$ increases mixing (![]() $\mathit {Pe}$) on both smooth and modified surfaces. The opposing effects of higher
$\mathit {Pe}$) on both smooth and modified surfaces. The opposing effects of higher ![]() $\mathit {Re}$ giving higher thermal resistance, but also increased mixing, can explain the complex trend of
$\mathit {Re}$ giving higher thermal resistance, but also increased mixing, can explain the complex trend of ![]() $\mathit {Nu}(\mathit {Re})$ seen in figure 7 on both smooth and modified surfaces.
$\mathit {Nu}(\mathit {Re})$ seen in figure 7 on both smooth and modified surfaces.
By taking the ratio ![]() $\mathit {Pe}_l/\mathit {Re}$ we obtain a measure for the efficiency of the surface topology at generating mixing for a given operating condition. The ratio can be reformulated as
$\mathit {Pe}_l/\mathit {Re}$ we obtain a measure for the efficiency of the surface topology at generating mixing for a given operating condition. The ratio can be reformulated as
to highlight the expected relations with ![]() $\mathit {Nu}$. Here, the ratio
$\mathit {Nu}$. Here, the ratio ![]() $u_{l,{std}} / V_l$ represents the effective mixing intensity in the film relative to the average streamwise film velocity and
$u_{l,{std}} / V_l$ represents the effective mixing intensity in the film relative to the average streamwise film velocity and ![]() $\delta _N / \delta _l$ is the laminar film thickness on a smooth surface to the actual average film thickness. The latter ratio therefore represents the change in the thermal resistance of the film due to, for example, liquid holdup by the surface modifications. A high
$\delta _N / \delta _l$ is the laminar film thickness on a smooth surface to the actual average film thickness. The latter ratio therefore represents the change in the thermal resistance of the film due to, for example, liquid holdup by the surface modifications. A high ![]() $\mathit {Pe}_l/\mathit {Re}$ thus represents a case with high mixing (high
$\mathit {Pe}_l/\mathit {Re}$ thus represents a case with high mixing (high ![]() $u_{l,{std}}$ gives high
$u_{l,{std}}$ gives high ![]() $\mathit {Nu}$), low thermal resistance (due to low
$\mathit {Nu}$), low thermal resistance (due to low ![]() $\delta _l$ that gives high
$\delta _l$ that gives high ![]() $\mathit {Nu}$) and low thermal diffusivity (high
$\mathit {Nu}$) and low thermal diffusivity (high ![]() $\mathit {Pr}_l$ give high
$\mathit {Pr}_l$ give high ![]() $\mathit {Nu}$ since both depend on
$\mathit {Nu}$ since both depend on ![]() $D_l$). We thus expect
$D_l$). We thus expect ![]() $\mathit {Nu}$ to increase with
$\mathit {Nu}$ to increase with ![]() $\mathit {Pe}_l/\mathit {Re}$. These quantities are shown in figure 18(c) and display indeed a fair collapse of all cases onto the line
$\mathit {Pe}_l/\mathit {Re}$. These quantities are shown in figure 18(c) and display indeed a fair collapse of all cases onto the line ![]() $0.3(\mathit {Pe}_l/\mathit {Re})^{0.35}$. The worst outlier is the case
$0.3(\mathit {Pe}_l/\mathit {Re})^{0.35}$. The worst outlier is the case ![]() $\mathit {Nu}=0.64$ at
$\mathit {Nu}=0.64$ at ![]() $\mathit {Re}=545$ from § 3.1 where we increased the surface tension (
$\mathit {Re}=545$ from § 3.1 where we increased the surface tension (![]() $\mathit {Ka}$) by a factor of
$\mathit {Ka}$) by a factor of ![]() $10$. The higher surface tension suppresses interface fluctuations and reduces
$10$. The higher surface tension suppresses interface fluctuations and reduces ![]() $\mathit {Pe}_l$. This case should therefore be compared with the others with caution.
$\mathit {Pe}_l$. This case should therefore be compared with the others with caution.
Figure 18(c) shows that smooth surfaces (circles) typically induce low relative mixing (low ![]() $\mathit {Pe}_l/\mathit {Re}$), while the modified surfaces (diamonds) induce relative mixing almost an order of magnitude larger, depending on the surface topology. The scaling of approximately
$\mathit {Pe}_l/\mathit {Re}$), while the modified surfaces (diamonds) induce relative mixing almost an order of magnitude larger, depending on the surface topology. The scaling of approximately ![]() $\mathit {Nu} \propto (\mathit {Pe}_l/\mathit {Re})^{0.35}$ found here is relatively close to the
$\mathit {Nu} \propto (\mathit {Pe}_l/\mathit {Re})^{0.35}$ found here is relatively close to the ![]() $\mathit {Nu} \propto \mathit {Pr}_l^{0.42}$ found in § 3.3.3 explaining why the cases from that section (with constant
$\mathit {Nu} \propto \mathit {Pr}_l^{0.42}$ found in § 3.3.3 explaining why the cases from that section (with constant ![]() $(u_{l,{std}} \delta _N) / (V_l \delta _l)$) follow the former scaling relatively well.
$(u_{l,{std}} \delta _N) / (V_l \delta _l)$) follow the former scaling relatively well.
In summary, the results presented in this section suggest that, in the investigated range of parameters, ![]() $\mathit {Nu}$ is governed by the balance of film mixing intensity, film thickness and thermal diffusivity. This holds for smooth and modified surfaces with varying topology. However, the modified surfaces induce significantly higher mixing at the same flow conditions which nearly doubles
$\mathit {Nu}$ is governed by the balance of film mixing intensity, film thickness and thermal diffusivity. This holds for smooth and modified surfaces with varying topology. However, the modified surfaces induce significantly higher mixing at the same flow conditions which nearly doubles ![]() $\mathit {Nu}$.
$\mathit {Nu}$.
4. Conclusions
We perform multiphase DNS and detailed heat flux analyses to explain the mechanisms behind the enhanced heat transfer rates in evaporative vertical falling films due to surface modifications. We formulate a heat flux decomposition and averaging method to quantify and analyse mean and fluctuating components of the advective and diffusive heat fluxes within the film. The combined analysis of instantaneous and average fields gives both a qualitative and quantitative picture of the underlying mechanisms behind the improved heat transfer on modified surfaces.
Based on our results, we propose in § 3.2 a hypothesis of four main synergistic mechanisms behind the heat transfer improvement: (i) the liquid in the interface region, which is relatively well mixed and cool, flows along the wall between the modifications and gets heated by high diffusive fluxes; (ii) upstream of the modification, the heated fluid is directed outward, around the modification; (iii) downstream of the modification, the relatively hot fluid also flows outward due to the presence of a recirculation zone; (iv) the hot fluid that flows outward mixes with the cooler fluid in the interface region because of the strong hydrodynamic fluctuations here. These four interacting mechanisms create a well-mixed and relatively hot interface region that gives higher evaporation rates compared with those for a smooth surface.
In addition, we present detailed parameter investigations of how important surface topology parameters (pitch ![]() $\hat {p}$ and height
$\hat {p}$ and height ![]() $\hat {h}$) and the liquid Prandtl number
$\hat {h}$) and the liquid Prandtl number ![]() $\mathit {Pr}_l$ influence the mode of heat transport and the overall heat transfer rate. In the investigated parameter ranges, we find, in § 3.3.1, that the pitch
$\mathit {Pr}_l$ influence the mode of heat transport and the overall heat transfer rate. In the investigated parameter ranges, we find, in § 3.3.1, that the pitch ![]() $\hat {p}/\delta _N=10$ (distance between modifications) maximises
$\hat {p}/\delta _N=10$ (distance between modifications) maximises ![]() $\mathit {Nu}(\,\hat {p})$ and that the optimal value is related to the length scale of the well-mixed zones induced by the modifications (mechanism 2 and 3) while still maintaining attached flow between modifications (enabling mechanism 1). The height
$\mathit {Nu}(\,\hat {p})$ and that the optimal value is related to the length scale of the well-mixed zones induced by the modifications (mechanism 2 and 3) while still maintaining attached flow between modifications (enabling mechanism 1). The height ![]() $\hat {h}$ of the modifications is, in § 3.3.2, found to influence the overall heat transfer rate as
$\hat {h}$ of the modifications is, in § 3.3.2, found to influence the overall heat transfer rate as ![]() $\mathit {Nu} \propto \hat {h}^{0.27}$. However, further analysis shows that, for
$\mathit {Nu} \propto \hat {h}^{0.27}$. However, further analysis shows that, for ![]() $\hat {h}/\delta _N>1$, the improvement is mainly due to the increased surface area. Since too large
$\hat {h}/\delta _N>1$, the improvement is mainly due to the increased surface area. Since too large ![]() $\hat {h}$ may cause unwanted sputtering/entrainment effects, the findings suggest
$\hat {h}$ may cause unwanted sputtering/entrainment effects, the findings suggest ![]() $\hat {h}$ should be maximised just below the occurrence of the unwanted phenomena to optimise
$\hat {h}$ should be maximised just below the occurrence of the unwanted phenomena to optimise ![]() $\mathit {Nu}(\hat {h})$. The length of the recirculation zone
$\mathit {Nu}(\hat {h})$. The length of the recirculation zone ![]() $L_r$ downstream the modifications is found to be proportional to
$L_r$ downstream the modifications is found to be proportional to ![]() $\hat {h}$ as
$\hat {h}$ as ![]() $L_r/\hat {h}\approx 3.5$. Since
$L_r/\hat {h}\approx 3.5$. Since ![]() $L_r$ is also related to the optimal pitch
$L_r$ is also related to the optimal pitch ![]() $\hat {p}$, these findings suggest a ratio
$\hat {p}$, these findings suggest a ratio ![]() $\hat {h}/\hat {p}=0.11$ is suitable to optimise
$\hat {h}/\hat {p}=0.11$ is suitable to optimise ![]() $\mathit {Nu}(\hat {p},\hat {h})$. In § 3.3.3, we find the relation
$\mathit {Nu}(\hat {p},\hat {h})$. In § 3.3.3, we find the relation ![]() $\mathit {Nu} \propto \mathit {Pr}_l^{0.42}$ for the values
$\mathit {Nu} \propto \mathit {Pr}_l^{0.42}$ for the values ![]() $\mathit {Pr}_l=(5,10,20)$. In these cases, the heat transfer is limited by diffusion at the wall and not the mixing (advection) in the film. Therefore, the optimal topology parameters for the surface modifications are not significantly dependent on
$\mathit {Pr}_l=(5,10,20)$. In these cases, the heat transfer is limited by diffusion at the wall and not the mixing (advection) in the film. Therefore, the optimal topology parameters for the surface modifications are not significantly dependent on ![]() $\mathit {Pr}_l$ at these relatively high values.
$\mathit {Pr}_l$ at these relatively high values.
Finally, we summarise our results, in § 3.4, by examining how important global dimensionless parameters can elucidate the governing phenomena for the overall heat transfer rate on smooth and modified surfaces. We compute the Péclet number that is ![]() $\mathit {Pe}_l \gg 1$ for all our cases indicating that the advective heat transport dominates the diffusive transport in the film. We would thus expect
$\mathit {Pe}_l \gg 1$ for all our cases indicating that the advective heat transport dominates the diffusive transport in the film. We would thus expect ![]() $\mathit {Nu}$ to monotonically increase with
$\mathit {Nu}$ to monotonically increase with ![]() $\mathit {Pe}_l$. However, a
$\mathit {Pe}_l$. However, a ![]() $\mathit {Re}$ number effect is observed where increasing the
$\mathit {Re}$ number effect is observed where increasing the ![]() $\mathit {Re}$ gives higher
$\mathit {Re}$ gives higher ![]() $\mathit {Pe}_l$ but not necessarily higher
$\mathit {Pe}_l$ but not necessarily higher ![]() $\mathit {Nu}$. This is explained by the fact that the film thickness increases with the flow rate
$\mathit {Nu}$. This is explained by the fact that the film thickness increases with the flow rate ![]() $\mathit {Re}$ (and thus the thermal resistance), but, in general,
$\mathit {Re}$ (and thus the thermal resistance), but, in general, ![]() $\mathit {Re}$ also increases the mixing (
$\mathit {Re}$ also increases the mixing (![]() $\mathit {Pe}_l$) of the film. Our results show that, for a given surface topology,
$\mathit {Pe}_l$) of the film. Our results show that, for a given surface topology, ![]() $\mathit {Re} \propto \mathit {Pe}_l^{1.3}$ and that the surface topology mainly influences the proportionality constant. By considering the ratio
$\mathit {Re} \propto \mathit {Pe}_l^{1.3}$ and that the surface topology mainly influences the proportionality constant. By considering the ratio ![]() $\mathit {Pe}_l/\mathit {Re}$ we obtain a measure for the efficiency of a surface to generate mixing at a given operation condition. All our cases on both smooth and modified surfaces with various topology parameters show a fair collapse on a line scaling approximately as
$\mathit {Pe}_l/\mathit {Re}$ we obtain a measure for the efficiency of a surface to generate mixing at a given operation condition. All our cases on both smooth and modified surfaces with various topology parameters show a fair collapse on a line scaling approximately as ![]() $\mathit {Nu} \propto (\mathit {Pe}_l/\mathit {Re})^{0.35}$ indicating
$\mathit {Nu} \propto (\mathit {Pe}_l/\mathit {Re})^{0.35}$ indicating ![]() $\mathit {Nu}$ is indeed governed by the balance of film mixing intensity, film thickness and thermal diffusivity in the investigated range of parameters.
$\mathit {Nu}$ is indeed governed by the balance of film mixing intensity, film thickness and thermal diffusivity in the investigated range of parameters.
This study extends our knowledge about the main mechanisms behind the heat transport improvement due to surface modifications. The modifications and governing parameters are industrially relevant (not only to the food and pulp and paper industries, but also to, for example, desalination applications) and our methodology and findings therefore facilitate guidelines for designing more efficient modified surfaces. The developed methodology is formulated in a general manner and can be used to study the heat transfer mechanisms for any type of surface modification. The general trends obtained in the present study involving the chosen model problem likely apply to similar topologies, such as trip wires, but future investigations are needed to investigate how and to what extent other types of surface modifications (such as wire meshes, vertical grooves or three-dimensional configurations) alter the heat transport mechanisms through the film. We do, however, expect the general trend of increasing ![]() $\mathit {Nu}$ with
$\mathit {Nu}$ with ![]() $(\mathit {Pe}_l/\mathit {Re})$ to hold. Further studies are also suggested to expand the investigated parameter ranges (including
$(\mathit {Pe}_l/\mathit {Re})$ to hold. Further studies are also suggested to expand the investigated parameter ranges (including ![]() $\mathit {Ka}$) and to study the effect of higher vapour-liquid relative velocities on the heat transport mechanisms and
$\mathit {Ka}$) and to study the effect of higher vapour-liquid relative velocities on the heat transport mechanisms and ![]() $\mathit {Nu}$.
$\mathit {Nu}$.
Funding
We acknowledge funding from the Swedish Energy Agency project P40550-3, Valmet AB and Tetra Pak CPS. The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS), partially funded by the Swedish Research Council through grant agreement no. 2022-06725.
Declaration of interests
The authors report no conflict of interest.