Published online by Cambridge University Press: 08 February 2012
The evolution of barotropic vortices over a topographic, axisymmetric mountain in a homogeneous rotating fluid is studied experimentally. The aim is to identify the main physical processes observed in (i) a horizontal plane of motion, perpendicular to the rotation axis of the system, and (ii) a vertical plane across the diameter of the mountain. The vortices are monopolar cyclones initially generated near or over the topography. Initially, the vortices drift towards the mountain due to the 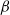 -effect associated with the topographic slope. On arriving, they turn around the obstacle in an anticyclonic direction, whilst anticyclonic vorticity is generated over the summit. The long-term vorticity distribution is dominated by the original cyclone elongated around the topographic contours and the generated anticyclone over the tip of the topography. In the vertical plane an oscillatory uphill–downhill flow is generated, which is directly related to the drift of the cyclone around the mountain. Depending on the vortex characteristics, the period of the oscillation ranges from 4 to 10 times the rotation period of the system. The horizontal and vertical flow fields are reproduced numerically by using a shallow-water formulation, which allows a detailed view of the vertical motions, hence facilitating the interpretation of the experimental results. In addition, the cyclone–anticyclone pair over the mountain is compared with analytical solutions of topographically trapped waves. A general conclusion is that vertical motions persist for several days (or rotation periods), which implies that this mechanism might be potentially important for the vertical transport over seamounts.
-effect associated with the topographic slope. On arriving, they turn around the obstacle in an anticyclonic direction, whilst anticyclonic vorticity is generated over the summit. The long-term vorticity distribution is dominated by the original cyclone elongated around the topographic contours and the generated anticyclone over the tip of the topography. In the vertical plane an oscillatory uphill–downhill flow is generated, which is directly related to the drift of the cyclone around the mountain. Depending on the vortex characteristics, the period of the oscillation ranges from 4 to 10 times the rotation period of the system. The horizontal and vertical flow fields are reproduced numerically by using a shallow-water formulation, which allows a detailed view of the vertical motions, hence facilitating the interpretation of the experimental results. In addition, the cyclone–anticyclone pair over the mountain is compared with analytical solutions of topographically trapped waves. A general conclusion is that vertical motions persist for several days (or rotation periods), which implies that this mechanism might be potentially important for the vertical transport over seamounts.