Article contents
A homogenised model for flow, transport and sorption in a heterogeneous porous medium
Published online by Cambridge University Press: 09 December 2021
Abstract
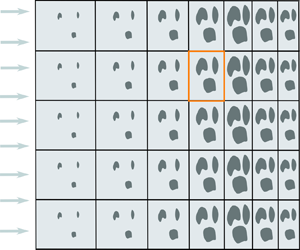
A major challenge in flow through porous media is to better understand the link between microstructure and macroscale flow and transport. For idealised microstructures, the mathematical framework of homogenisation theory can be used for this purpose. Here, we consider a two-dimensional microstructure comprising an array of obstacles of smooth but arbitrary shape, the size and spacing of which can vary along the length of the porous medium. We use homogenisation via the method of multiple scales to systematically upscale a novel problem involving cells of varying area to obtain effective continuum equations for macroscale flow and transport. The equations are characterised by the local porosity, a local anisotropic flow permeability, an effective local anisotropic solute diffusivity and an effective local adsorption rate. These macroscale properties depend non-trivially on the two degrees of microstructural geometric freedom in our problem: obstacle size and obstacle spacing. We exploit this dependence to construct and compare scenarios where the same porosity profile results from different combinations of obstacle size and spacing. We focus on a simple example geometry comprising circular obstacles on a rectangular lattice, for which we numerically determine the macroscale permeability and effective diffusivity. We investigate scenarios where the porosity is spatially uniform but the permeability and diffusivity are not. Our results may be useful in the design of filters or for studying the impact of deformation on transport in soft porous media.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
This author contributed significantly to this work.
References
REFERENCES
- 7
- Cited by



