Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T06:25:13.153Z Has data issue: false hasContentIssue false
  • English
  • Français

History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers

Published online by Cambridge University Press:  12 May 2017

A. Bobke ,
R. Vinuesa Open the ORCID record for R. Vinuesa [Opens in a new window] ,
R. Örlü Open the ORCID record for R. Örlü [Opens in a new window]  and
P. Schlatter Open the ORCID record for P. Schlatter [Opens in a new window]
A. Bobke
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden Swedish e-Science Research Centre (SeRC), Stockholm, Sweden
R. Vinuesa*
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden Swedish e-Science Research Centre (SeRC), Stockholm, Sweden
R. Örlü
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
P. Schlatter
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden Swedish e-Science Research Centre (SeRC), Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulent boundary layers under adverse pressure gradients are studied using well-resolved large-eddy simulations (LES) with the goal of assessing the influence of the streamwise pressure-gradient development. Near-equilibrium boundary layers were characterized through the Clauser pressure-gradient parameter 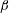$\unicode[STIX]{x1D6FD}$. In order to fulfil the near-equilibrium conditions, the free stream velocity was prescribed such that it followed a power-law distribution. The turbulence statistics pertaining to cases with a constant value of 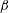$\unicode[STIX]{x1D6FD}$ (extending up to approximately 40 boundary-layer thicknesses) were compared with cases with non-constant 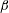$\unicode[STIX]{x1D6FD}$ distributions at matched values of 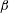$\unicode[STIX]{x1D6FD}$ and friction Reynolds number 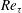$Re_{\unicode[STIX]{x1D70F}}$. An additional case at matched Reynolds number based on displacement thickness 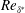$Re_{\unicode[STIX]{x1D6FF}^{\ast }}$ was also considered. It was noticed that non-constant 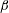$\unicode[STIX]{x1D6FD}$ cases appear to approach the conditions of equivalent constant 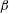$\unicode[STIX]{x1D6FD}$ cases after long streamwise distances (approximately 7 boundary-layer thicknesses). The relevance of the constant 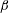$\unicode[STIX]{x1D6FD}$ cases lies in the fact that they define a ‘canonical’ state of the boundary layer, uniquely characterized by 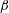$\unicode[STIX]{x1D6FD}$ and 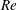$Re$. The investigations on the flat plate were extended to the flow around a wing section overlapping in terms of 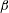$\unicode[STIX]{x1D6FD}$ and 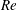$Re$. Comparisons with the flat-plate cases at matched values of 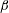$\unicode[STIX]{x1D6FD}$ and 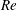$Re$ revealed that the different development history of the turbulent boundary layer on the wing section leads to a less pronounced wake in the mean velocity as well as a weaker second peak in the Reynolds stresses. This is due to the weaker accumulated effect of the 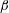$\unicode[STIX]{x1D6FD}$ history. Furthermore, a scaling law suggested by Kitsios et al. (Intl J. Heat Fluid Flow, vol. 61, 2016, pp. 129–136), proposing the edge velocity and the displacement thickness as scaling parameters, was tested on two constant-pressure-gradient parameter cases. The mean velocity and Reynolds-stress profiles were found to be dependent on the downstream development. The present work is the first step towards assessing history effects in adverse-pressure-gradient turbulent boundary layers and highlights the fact that the values of the Clauser pressure-gradient parameter and the Reynolds number are not sufficient to characterize the state of the boundary layer.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 820 , 10 June 2017 , pp. 667 - 692
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H., Örlü, R. & Segalini, A. 2012 A new formulation for the streamwise turbulence intensity distribution in wall-bounded turbulent flows. Eur. J. Mech. (B/Fluids) 36, 167–175.CrossRefGoogle Scholar
Alfredsson, P. H., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the ‘outer’ peak. Phys. Fluids 23, 041702.Google Scholar
Atkinson, C., Buchner, A. J., Eisfelder, M., Kitsios, V. & Soria, J. 2016 Time-resolved PIV measurements of a self-similar adverse pressure gradient turbulent boundary layer. In Proceedings of the 18th International Symposium on the Application of Laser and Imaging Techniques to Fluid Mechanics, Lisbon, Portugal.Google Scholar
Bailey, S. C. C., Hultmark, M., Monty, J. P., Alfredsson, P. H., Chong, M. S., Duncan, R. D., Fransson, J. H. M., Hutchins, N., Marusic, I., Mckeon, B. J. et al. 2013 Obtaining accurate mean velocity measurements in high Reynolds number turbulent boundary layers using Pitot tubes. J. Fluid Mech. 715, 642–670.Google Scholar
Bobke, A., Örlü, R. & Schlatter, P. 2016a Simulations of turbulent asymptotic suction boundary layers. J. Turbul. 17, 155–178.Google Scholar
Bobke, A., Vinuesa, R., Örlü, R. & Schlatter, P. 2016b Large-eddy simulations of adverse pressure gradient turbulent boundary layers. J. Phys.: Conf. Ser. 708, 012012.Google Scholar
Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S.2007 A pseudospectral solver for incompressible boundary layer. Tech. Rep. TRITA-MEK 2007:07. KTH Mechanics.Google Scholar
Eitel-Amor, G., Örlü, R. & Schlatter, P. 2014 Simulation and validation of a spatially evolving turbulent boundary layer up to Re 𝜃 = 8300. Intl J. Heat Fluid Flow 47, 57–69.CrossRefGoogle Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 NEK5000: open source spectral element CFD solver. Available at: http://nek5000.mcs.anl.gov.Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.Google Scholar
Hosseini, S. M., Vinuesa, R., Schlatter, P., Hanifi, A. & Henningson, D. S. 2016 Direct numerical simulation of the flow around a wing section at moderate Reynolds number. Intl J. Heat Fluid Flow 61, 117–128.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Kitsios, V., Atkinson, C., Sillero, J. A., Borrell, G., Gungor, A. G., Jiménez, J. & Soria, J. 2016 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer. Intl J. Heat Fluid Flow 61, 129–136.Google Scholar
Lee, J. H. 2017 Large-scale motions in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 810, 323–361.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2009 Structures in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 639, 101–131.CrossRefGoogle Scholar
Maciel, Y., Rossignol, K.-S. & Lemay, J. 2006 Self-similarity in the outer region of adverse-pressure-gradient turbulent boundary layers. AIAA J. 44, 2450–2464.Google Scholar
Marusic, I., Chauhan, K. A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.CrossRefGoogle Scholar
Marusic, I., Mckeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.CrossRefGoogle Scholar
Mellor, G. L. & Gibson, D. M. 1966 Equilibrium turbulent boundary layers. J. Fluid Mech. 24, 225–253.CrossRefGoogle Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2007 Self-consistent high-Reynolds-number asymptotics for zero-pressure-gradient turbulent boundary layers. Phys. Fluids 19, 115101.Google Scholar
Monty, J. P., Harun, Z. & Marusic, I. 2011 A parametric study of adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 32, 575–585.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.Google Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A. 2007 Approach to an asymptotic state for zero pressure gradient turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 365, 755–770.Google Scholar
Perry, A. E., Marusic, I. & Jones, M. B. 2002 On the streamwise evolution of turbulent boundary layers in arbitrary pressure gradients. J. Fluid Mech. 461, 61–91.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers. Inflow length and tripping effects. J. Fluid Mech. 710, 5–34.Google Scholar
Schlatter, P., Örlü, R., Li, Q., Brethouwer, G., Fransson, J. H. M., Johansson, A. V., Alfredsson, P. H. & Henningson, D. S. 2009 Turbulent boundary layers up to Re 𝜃 = 2500 studied through simulation and experiment. Phys. Fluids 21, 051702.CrossRefGoogle Scholar
Schlatter, P., Stolz, S. & Kleiser, L. 2004 LES of transitional flows using the approximate deconvolution model. Intl J. Heat Fluid Flow 25, 549–558.Google Scholar
Skote, M.2001 Studies of turbulent boundary layer flow through direct numerical simulation. PhD thesis, Royal Institute of Technology, Stockholm, Sweden.Google Scholar
Skote, M. & Henningson, D. S. 2002 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 471, 107–136.Google Scholar
Skote, M., Henningson, D. S. & Henkes, R. A. W. M. 1998 Direct numerical simulation of self-similar turbulent boundary layers in adverse pressure gradients. Flow Turbul. Combust. 60, 47–85.Google Scholar
Skåre, P. E. & Krogstad, P.-Å. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.CrossRefGoogle Scholar
Spalart, P. R. & Watmuff, J. H. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 249, 337–371.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vinuesa, R., Bobke, A., Örlü, R. & Schlatter, P. 2016 On determining characteristic length scales in pressure-gradient turbulent boundary layers. Phys. Fluids 28, 055101.Google Scholar
Vinuesa, R., Örlü, R. & Schlatter, P. 2017 Characterisation of backflow events over a wing section. J. Turbul. 18, 170–185.Google Scholar
Vinuesa, R., Rozier, P. H., Schlatter, P. & Nagib, H. M. 2014 Experiments and computations of localized pressure gradients with different history effects. AIAA J. 55, 368–384.Google Scholar