Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-09T22:02:45.508Z Has data issue: false hasContentIssue false
  • English
  • Français

High-speed granular chute flows

Published online by Cambridge University Press:  31 August 2012

Alex J. Holyoake  and
Jim N. McElwaine
Alex J. Holyoake*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Jim N. McElwaine
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper reports experimental findings on the flow of sand down a steep chute. Nearly all granular flow models have a maximum value for the friction and therefore predict that flows on steep slopes will accelerate at a constant rate until the interaction with the ambient fluid becomes important. This prediction has not been tested by previous work, which has focused on relatively low slope angles where steady, fully developed flows occur after short distances. We test this by investigating flows over a much greater range of slope angles (30–50) and flow depths (4–130 particle diameters). We examine flows with two basal conditions, one flat and frictional, the other bumpy. The latter imposes a no-slip condition for slow, deep flows, but permits some degree of slip for high flow velocities. The data suggests that friction can be much larger than theories such as the 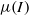rheology proposed by Jop, Forterre & Pouliquen (Nature, vol. 441, 2006) suggest and that there may be constant velocity states above the angle of vanishing 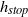. Although these flows do not vary in time, all but the flows on the bumpy base at low inclinations accelerate down the slope. A recirculation mechanism sustains flows with a maximum mass flux of 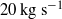, allowing observations to be made at multiple points for each flow for an indefinite period. Flows with Froude number in the range 0.1–25 and bulk inertial number 0.1–2.7 were observed in the dense regime, with surface velocities in the range 0.2–5.6 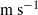. Previous studies have focused on 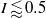. We show that a numerical implementation of the 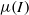rheology does not fully capture the accelerating dynamics or the transverse velocity profile on the bumpy base. We also observe the transverse separation of the flow into a dense core flanked by dilute regions and the formation of longitudinal vortices.

JFM classification

Non-Newtonian Flows: Rheology Granular media: Granular media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 35 - 71
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ahn, H., Brennen, C. E. & Sabersky, R. H. 1991 Measurements of velocity, velocity fluctuation, density, and stresses in chute flows of granular materials. J. Appl. Mech. 58 (792), 12.CrossRefGoogle Scholar
2. Ahn, H., Brennen, C. E. & Sabersky, R. H. 1992 Analysis of the fully developed chute flow of granular materials. J. Appl. Mech. 59, 109.CrossRefGoogle Scholar
3. Ancey, C., Coussot, P. & Evesque, P. 1999 A theoretical framework for granular suspensions in a steady simple shear flow. J. Rheol. 43, 1673.CrossRefGoogle Scholar
4. Baran, O., Ertaş, D., Halsey, T. C., Grest, G. S. & Lechman, J. B. 2006 Velocity correlations in dense gravity-driven granular chute flow. Phys. Rev. E 74 (5), 051302.CrossRefGoogle ScholarPubMed
5. Börzsönyi, T. & Ecke, R. E. 2006 Rapid granular flows on a rough incline: phase diagram, gas transition, and effects of air drag. Phys. Rev. E 74 (6), 061301.CrossRefGoogle ScholarPubMed
6. Börzsönyi, T., Ecke, R. E. & McElwaine, J. N. 2009 Patterns in flowing sand: understanding the physics of granular flow. Phys. Rev. Lett. 103 (17), 178302.CrossRefGoogle ScholarPubMed
7. Delannay, R., Louge, M., Richard, P., Taberlet, N. & Valance, A. 2007 Towards a theoretical picture of dense granular flows down inclines. Nat. Mater. 6 (2), 99–108.CrossRefGoogle ScholarPubMed
8. Ertaş, D., Grest, G. S., Halsey, T. C., Levine, D. & Silbert, L. E. 2001 Gravity-driven dense granular flows. Europhys. Lett. 56, 214.CrossRefGoogle Scholar
9. Forterre, Y. 2006 Kapiza waves as a test for three-dimensional granular flow rheology. J. Fluid Mech. 563, 123–132.CrossRefGoogle Scholar
10. Forterre, Y. & Pouliquen, O. 2001 Longitudinal vortices in granular flows. Phys. Rev. Lett. 86 (26), 5886–5889.CrossRefGoogle ScholarPubMed
11. Forterre, Y. & Pouliquen, O. 2003 Long-surface-wave instability in dense granular flows. J. Fluid Mech. 486, 21–50.CrossRefGoogle Scholar
12. Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40 (1), 1–24.CrossRefGoogle Scholar
13. Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267–293.CrossRefGoogle Scholar
14. Gray, J., Wieland, M. & Hutter, K. 1985 Gravity-driven free surface flow of granular avalanches over complex basal topography. Proc. R. Soc. Lond. Ser. A: Math. Phys. Engng Sci. 455, 1841.CrossRefGoogle Scholar
15. Jackson, R. 1983 Some mathematical and physical aspects of continuum models for the motion of granular materials. In Theory of Dispersed Multiphase Flow (ed. Meyer, R. ). MRC Seminar, May 1982 , Academic Press.Google Scholar
16. Janssen, H. A. 1895 Tests on grain pressure silos. Z. Verein. Deutsch. Ing. 39 (35), 1045–1049.Google Scholar
17. Jenkins, J. & Berzi, D. 2010 Dense inclined flows of inelastic spheres: tests of an extension of kinetic theory. Granul. Matt. 12, 151–158.CrossRefGoogle Scholar
18. Jenkins, J. T. & Richman, M. W. 1985 Kinetic theory for plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 28, 3485.CrossRefGoogle Scholar
19. Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.CrossRefGoogle Scholar
20. Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441.CrossRefGoogle ScholarPubMed
21. Louge, M. Y. & Keast, S. C. 2001 On dense granular flows down flat frictional inclines. Phys. Fluids 13, 1213.CrossRefGoogle Scholar
22. McNamara, S. & Young, W. R. 1994 Inelastic collapse in two dimensions. Phys. Rev. E 50, 28–31.CrossRefGoogle ScholarPubMed
23. MiDi, G. D. R. 2004 On dense granular flows. Eur. Phys. J. E: Soft Matter Biol. Phys. 14 (4), 341–365.CrossRefGoogle Scholar
24. Mitarai, N. & Nakanishi, H. 2005 Bagnold scaling, density plateau, and kinetic theory analysis of dense granular flow. Phys. Rev. Lett. 94, 128001.CrossRefGoogle ScholarPubMed
25. Nedderman, R. M., Tuzun, U., Savage, S. B. & Houlsby, G. T. 1982 The flow of granular materials–i: discharge rates from hoppers. Chem. Engng Sci. 37 (11), 1597–1609.CrossRefGoogle Scholar
26. Patton, J. S., Brennen, C. E. & Sabersky, R. H. 1987 Shear flows of rapidly flowing granular materials. J. Appl. Mech. 54, 801.CrossRefGoogle Scholar
27. Pouliquen, O. 1999 Scaling laws in granular flows down rough inclined planes. Phys. Fluids 11, 542.CrossRefGoogle Scholar
28. Pouliquen, O., Cassar, C., Jop, P., Forterre, Y. & Nicolas, M. 2006 Flow of dense granular material: towards simple constitutive laws. J. Stat. Mech.: Theory Exp. 2006, P07020.CrossRefGoogle Scholar
29. Savage, S. B. 1979 Gravity flow of cohesionless granular materials in chutes and channels. J. Fluid Mech. 92 (1), 53–96.CrossRefGoogle Scholar
30. Savage, S. B. 1984 The mechanics of rapid granular flows. Adv. Appl. Mech. 24, 289–366.CrossRefGoogle Scholar
31. Savage, S. B. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 199, 177–215.CrossRefGoogle Scholar
32. Silbert, L. E., Ertaş, D., Grest, G. S., Halsey, T. C., Levine, D. & Plimpton, S. J. 2001 Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E 64 (5), 51302.CrossRefGoogle ScholarPubMed
33. Sveen, J. K. & Dalziel, S. B. 2005 A dynamic masking technique for combined measurements of PIV and synthetic schlieren applied to internal gravity waves. Meas. Sci. Technol. 16, 1954–1960.CrossRefGoogle Scholar
34. Taberlet, N., Richard, P., Jenkins, J. T. & Delannay, R. 2007 Density inversion in rapid granular flows: the supported regime. Eur. Phys. J. E 22 (1), 17–24.CrossRefGoogle ScholarPubMed
35. Taberlet, N., Richard, P., Valance, A., Losert, W., Pasini, J. M., Jenkins, J. T. & Delannay, R. 2003 Superstable granular heap in a thin channel. Phys. Rev. Lett. 91 (26), 264301.CrossRefGoogle Scholar
36. White, D. J. 2003 PSD measurement using the single particle optical sizing (SPOS) method. Géotechnique 53 (3), 317–326.CrossRefGoogle Scholar