Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T22:44:47.208Z Has data issue: false hasContentIssue false
  • English
  • Français

High-resolution velocity measurement in the inner part of turbulent boundary layers over super-hydrophobic surfaces

Published online by Cambridge University Press:  26 July 2016

Hangjian Ling ,
Siddarth Srinivasan Open the ORCID record for Siddarth Srinivasan [Opens in a new window] ,
Kevin Golovin Open the ORCID record for Kevin Golovin [Opens in a new window] ,
Gareth H. McKinley ,
Anish Tuteja  and
Joseph Katz
Hangjian Ling
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Siddarth Srinivasan
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Kevin Golovin
Affiliation:
Department of Materials Science and Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Gareth H. McKinley
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Anish Tuteja
Affiliation:
Department of Materials Science and Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Joseph Katz*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Digital holographic microscopy is used for characterizing the profiles of mean velocity, viscous and Reynolds shear stresses, as well as turbulence level in the inner part of turbulent boundary layers over several super-hydrophobic surfaces (SHSs) with varying roughness/texture characteristics. The friction Reynolds numbers vary from 693 to 4496, and the normalized root mean square values of roughness 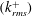$(k_{rms}^{+})$ vary from 0.43 to 3.28. The wall shear stress is estimated from the sum of the viscous and Reynolds shear stress at the top of roughness elements and the slip velocity is obtained from the mean profile at the same elevation. For flow over SHSs with 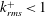$k_{rms}^{+}<1$, drag reduction and an upward shift of the mean velocity profile occur, along with a mild increase in turbulence in the inner part of the boundary layer. As the roughness increases above 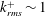$k_{rms}^{+}\sim 1$, the flow over the SHSs transitions from drag reduction, where the viscous stress dominates, to drag increase where the Reynolds shear stress becomes the primary contributor. For the present maximum value of 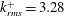$k_{rms}^{+}=3.28$, the inner region exhibits the characteristics of a rough wall boundary layer, including elevated wall friction and turbulence as well as a downward shift in the mean velocity profile. Increasing the pressure in the test facility to a level that compresses the air layer on the SHSs and exposes the protruding roughness elements reduces the extent of drag reduction. Aligning the roughness elements in the streamwise direction increases the drag reduction. For SHSs where the roughness effect is not dominant (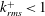$k_{rms}^{+}<1$), the present measurements confirm previous theoretical predictions of the relationships between drag reduction and slip velocity, allowing for both spanwise and streamwise slip contributions.

JFM classification

Flow Control: Drag reduction Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 670 - 703
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aljallis, E., Sarshar, M. A., Datla, R., Sikka, V., Jones, A. & Choi, C.-H. 2013 Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 25 (2), 025103.Google Scholar
Antonia, R. A. & Luxton, R. E. 1971 The response of a turbulent boundary layer to a step change in surface roughness. Part 1. Smooth to rough. J. Fluid Mech. 48 (04), 721–761.Google Scholar
Bidkar, R. A., Leblanc, L., Kulkarni, A. J., Bahadur, V., Ceccio, S. L. & Perlin, M. 2014 Skin-friction drag reduction in the turbulent regime using random-textured hydrophobic surfaces. Phys. Fluids 26 (8), 085108.Google Scholar
Brzek, B. G., Cal, R. B., Johansson, G. & Castillo, L. 2008 Transitionally rough zero pressure gradient turbulent boundary layers. Exp. Fluids 44 (1), 115–124.CrossRefGoogle Scholar
Busse, A. & Sandham, N. D. 2012 Influence of an anisotropic slip-length boundary condition on turbulent channel flow. Phys. Fluids 24 (5), 055111.CrossRefGoogle Scholar
Busse, A. & Sandham, N. D. 2013 Turbulent flow over superhydrophobic surfaces – roughness versus slip. In 14th European Turbulence Conference, Lyon, France.Google Scholar
Ceccio, S. L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42 (1), 183–203.CrossRefGoogle Scholar
Chan, L., Macdonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.CrossRefGoogle Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.Google Scholar
Daniello, R. J., Waterhouse, N. E. & Rothstein, J. P. 2009 Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids 21 (8), 085103.Google Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Dean, R. B. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. Trans. ASME J. Fluids Engng 100 (2), 215–223.CrossRefGoogle Scholar
Denis, L., Fournier, C., Fournel, T. & Ducottet, C. 2005 Twin-image noise reduction by phase retrieval in in-line digital holography. Proc. SPIE 5914, 59140J1–59140J14.Google Scholar
Ferrante, A. & Elghobashi, S. 2004 On the physical mechanisms of drag reduction in a spatially developing turbulent boundary layer laden with microbubbles. J. Fluid Mech. 503, 345–355.CrossRefGoogle Scholar
Fukagata, K., Kasagi, N. & Koumoutsakos, P. 2006 A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces. Phys. Fluids 18 (5), 051703.Google Scholar
García-Mayoral, R. & Jiménez, J. 2011 Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.Google Scholar
Gopalan, S. & Katz, J. 2000 Flow structure and modeling issues in the closure region of attached cavitation. Phys. Fluids 12 (4), 895–911.CrossRefGoogle Scholar
Greidanus, A. J., Delfos, R. & Westerweel, J. 2011 Drag reduction by surface treatment in turbulent Taylor–Couette flow. J. Phys.: Conf. Ser. 318 (8), 082016.Google Scholar
Hasegawa, Y., Frohnapfel, B. & Kasagi, N. 2011 Effects of spatially varying slip length on friction drag reduction in wall turbulence. J. Phys.: Conf. Ser. 318 (2), 022028.Google Scholar
Henoch, C., Krupenkin, T., Kolodner, P., Taylor, J., Hodes, M., Lynos, A., Peguero, C. & Breuer, K. 2006 Turbulent drag reduction using superhydrophobic surfaces. In 3rd AIAA Flow Control Conference, pp. 1–5. American Institute of Aeronautics and Astronautics.Google Scholar
Hong, J., Katz, J. & Schultz, M. P. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.Google Scholar
Jeffs, K., Maynes, D. & Webb, B. W. 2010 Prediction of turbulent channel flow with superhydrophobic walls consisting of micro-ribs and cavities oriented parallel to the flow direction. Intl J. Heat Mass Transfer 53 (4), 786–796.Google Scholar
Jelly, T. O., Jung, S. Y. & Zaki, T. A. 2014 Turbulence and skin friction modification in channel flow with streamwise-aligned superhydrophobic surface texture. Phys. Fluids 26 (9), 095102.CrossRefGoogle Scholar
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36 (1), 173–196.CrossRefGoogle Scholar
Jung, Y. C. & Bhushan, B. 2010 Biomimetic structures for fluid drag reduction in laminar and turbulent flows. J. Phys.: Condens. Matter 22 (3), 035104.Google ScholarPubMed
Katz, J. & Sheng, J. 2010 Applications of holography in fluid mechanics and particle dynamics. Annu. Rev. Fluid Mech. 42, 531–555.Google Scholar
Lee, S.-H. & Sung, H. J. 2007 Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J. Fluid Mech. 584, 125–146.CrossRefGoogle Scholar
Ligrani, P. M. & Moffat, R. J. 1986 Structure of transitionally rough and fully rough turbulent boundary layers. J. Fluid Mech. 162, 69–98.CrossRefGoogle Scholar
Ling, H. & Katz, J. 2014 Separating twin images and locating the center of a microparticle in dense suspensions using correlations among reconstructed fields of two parallel holograms. Appl. Opt. 53 (27), G1–G11.Google Scholar
Liu, K., Tian, Y. & Jiang, L. 2013 Bio-inspired superoleophobic and smart materials: design, fabrication, and application. Prog. Mater. Sci. 58 (4), 503–564.CrossRefGoogle Scholar
Liu, X. & Katz, J. 2006 Instantaneous pressure and material acceleration measurements using a four-exposure PIV system. Exp. Fluids 41 (2), 227–240.Google Scholar
Liu, X. & Katz, J. 2013 Vortex–corner interactions in a cavity shear layer elucidated by time-resolved measurements of the pressure field. J. Fluid Mech. 728, 417–457.Google Scholar
Martell, M. B., Perot, J. B. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31–41.Google Scholar
Martell, M. B., Rothstein, J. P. & Perot, J. B. 2010 An analysis of superhydrophobic turbulent drag reduction mechanisms using direct numerical simulation. Phys. Fluids 22 (6), 1–13.Google Scholar
Min, T. & Kim, J. 2004 Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 16 (7), L55–L58.CrossRefGoogle Scholar
Park, H.2015 A numerical study of the effects of superhydrophobic surfaces on skin-friction drag reduction in wall-bounded shear flows. PhD thesis, University of California, Los Angeles.Google Scholar
Park, H., Park, H. & Kim, J. 2013a A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25 (11), 110815.Google Scholar
Park, H., Sun, G. Y. & Kim, C. J. 2013b Turbulent drag reduction on superhydrophobic surfaces confirmed by built-in shear sensing. In Micro Electro Mechanical Systems (MEMS), IEEE 26th International Conference, Taipei, pp. 1183–1186.Google Scholar
Park, H., Sun, G. Y. & Kim, C. J. 2014 Superhydrophobic turbulent drag reduction as a function of surface grating parameters. J. Fluid Mech. 747, 722–734.Google Scholar
Peguero, C. & Breuer, K. 2009 On drag reduction in turbulent channel flow over superhydrophobic surfaces. Advances in Turbulence XII: 12th EUROMECH European Turbulence Conference pp. 233–236.Google Scholar
Roth, G. I. & Katz, J. 2001 Five techniques for increasing the speed and accuracy of PIV interrogation. Meas. Sci. Technol. 12 (3), 238–245.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Saito, N. & Pullin, D. I. 2014 Large eddy simulation of smooth–rough–smooth transitions in turbulent channel flows. Intl J. Heat Mass Transfer 78, 707–720.Google Scholar
Samaha, M. A., Tafreshi, H. & Gad-el-Hak, M. 2012 Influence of flow on longevity of superhydrophobic coatings. Langmuir 28 (25), 9759–9766.Google Scholar
Samaha, M. A., Vahedi Tafreshi, H. & Gad-el-Hak, M. 2011 Modeling drag reduction and meniscus stability of superhydrophobic surfaces comprised of random roughness. Phys. Fluids 23 (1), 012001.Google Scholar
Schultz, M. P. & Flack, K. A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.Google Scholar
Seo, J., García-Mayoral, R. & Mani, A. 2015 Pressure fluctuations and interfacial robustness in turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 783, 448–473.Google Scholar
Seo, J. & Mani, A. 2016 On the scaling of the slip velocity in turbulent flows over superhydrophobic surfaces. Phys. Fluids 28 (2), 025110.Google Scholar
Sheng, J., Malkiel, E. & Katz, J. 2008 Using digital holographic microscopy for simultaneous measurements of 3D near wall velocity and wall shear stress in a turbulent boundary layer. Exp. Fluids 45 (6), 1023–1035.CrossRefGoogle Scholar
Shirtcliffe, N. J., McHale, G. & Newton, M. I. 2011 The superhydrophobicity of polymer surfaces: recent developments. J. Polym. Sci. B 49 (17), 1203–1217.CrossRefGoogle Scholar
Shockling, M. A., Allen, J. J. & Smits, A. J. 2006 Roughness effects in turbulent pipe flow. J. Fluid Mech. 564, 267–285.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to R 𝜃 = 1410. J. Fluid Mech. 187, 61–98.Google Scholar
Srinivasan, S., Chhatre, S. S., Mabry, J. M., Cohen, R. E. & McKinley, G. H. 2011 Solution spraying of poly(methyl methacrylate) blends to fabricate microtextured, superoleophobic surfaces. Polymer 52 (14), 3209–3218.Google Scholar
Srinivasan, S., Kleingartner, J. A., Gilbert, J. B., Cohen, R. E., Milne, A. J. B. & McKinley, G. H. 2015 Sustainable drag reduction in turbulent Taylor–Couette flows by depositing sprayable superhydrophobic surfaces. Phys. Rev. Lett. 114 (1), 1–5.CrossRefGoogle ScholarPubMed
Talapatra, S. & Katz, J. 2013 Three-dimensional velocity measurements in a roughness sublayer using microscopic digital in-line holography and optical index matching. Meas. Sci. Technol. 24 (2), 024004.Google Scholar
Tian, H., Zhang, J., Wang, E., Yao, Z. & Jiang, N. 2015 Experimental investigation on drag reduction in turbulent boundary layer over superhydrophobic surface by TRPIV. Theor. Appl. Mech. Lett. 5 (1), 45–49.Google Scholar
Ünal, U. O., Ünal, B. & Atlar, M. 2012 Turbulent boundary layer measurements over flat surfaces coated by nanostructured marine antifoulings. Exp. Fluids 52 (6), 1431–1448.Google Scholar
Vajdi Hokmabad, B. & Ghaemi, S. 2016 Turbulent flow over wetted and non-wetted superhydrophobic counterparts with random structure. Phys. Fluids 28 (1), 015112.Google Scholar
Watanabe, K., Udagawa, Y. & Udagawa, H. 1999 Drag reduction of Newtonian fluid in a circular pipe with a highly water-repellent wall. J. Fluid Mech. 381, 225–238.Google Scholar
Woolford, B., Prince, J., Maynes, D. & Webb, B. W. 2009 Particle image velocimetry characterization of turbulent channel flow with rib patterned superhydrophobic walls. Phys. Fluids 21 (8), 085106.Google Scholar
Yang, J., Zhang, Z., Xu, X., Men, X., Zhu, X. & Zhou, X. 2011 Superoleophobic textured aluminum surfaces. New J. Chem. 35, 2422–2426.CrossRefGoogle Scholar
You, D. & Moin, P. 2007 Effects of hydrophobic surfaces on the drag and lift of a circular cylinder. Phys. Fluids 19 (8), 081701.Google Scholar
Zhao, J., Du, X. & Shi, X. 2007 Experimental research on friction-reduction with super-hydrophobic surfaces. J. Mar. Sci. Appl. 6 (3), 58–61.Google Scholar

Ling supplementary movie

Sample original holograms recorded at 20 kHz in the JHU water tunnel showing a sample plastron for a turbulent boundary over SHSPor, a porous substrate spray-coated with F-POSS/PMMA. The rms value of roughness height is 10 μm, the freestream velocity is 2.2 m/s, the friction Reynolds number is 1408, and the pressure difference across the porous base is 12 kPa (higher above the SHS). Image size: 9.3 mm x 2.5 mm.

Download Ling supplementary movie(Video)
Video 7.5 MB

Ling supplementary movie

Sample original holograms recorded at 20 kHz in the JHU water tunnel showing a sample plastron for a turbulent boundary over SHSPor, a porous substrate spray-coated with F-POSS/PMMA. The rms value of roughness height is 10 μm, the freestream velocity is 4.3 m/s, the friction Reynolds number is about 2850, and the pressure difference across the porous base is 6 kPa (higher above the SHS). Image size: 9.3 mm x 2.5 mm.

Download Ling supplementary movie(Video)
Video 7.7 MB

Ling supplementary movie

Sample original holograms recorded at 20 kHz in the JHU water tunnel showing a sample plastron for a turbulent boundary over SHSPor, a porous substrate spray-coated with F-POSS/PMMA. The rms value of roughness height is 10 μm, the freestream velocity is 6.4 m/s, the friction Reynolds number is 4287, and the pressure difference across the porous base is -4 kPa (higher below the SHS). Image size: 9.3 mm x 2.5 mm.

Download Ling supplementary movie(Video)
Video 8.4 MB