Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T20:09:07.509Z Has data issue: false hasContentIssue false
  • English
  • Français

High-order strongly nonlinear long wave approximation and solitary wave solution

Published online by Cambridge University Press:  18 July 2022

Wooyoung Choi Open the ORCID record for Wooyoung Choi [Opens in a new window]
Wooyoung Choi*
Affiliation:
Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, NJ 07102-1982, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

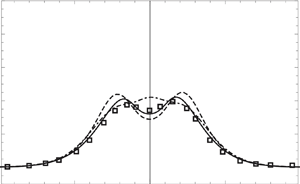
We consider high-order strongly nonlinear long wave models expanded in a single small parameter measuring the ratio of the water depth to the characteristic wavelength. By examining its dispersion relation, the high-order system for the bottom velocity is found stable to all disturbances at any order of approximation. On the other hand, systems for other velocities can be unstable and even ill-posed, as signified by the unbounded maximum growth. Under the steady assumption, a new third-order solitary wave solution of the Euler equations is obtained using the high-order strongly nonlinear system and is expanded in an amplitude parameter, which is different from that used in weakly nonlinear theory. The third-order solution is shown to well describe various physical quantities induced by a finite-amplitude solitary wave, including the wave profile, horizontal velocity profile, particle velocity at the crest and bottom pressure. For numerical computations, the first- and second-order strongly nonlinear systems for the bottom velocity are considered. It is shown that finite difference schemes are unstable due to truncation errors introduced in approximating high-order spatial derivatives and, therefore, a more accurate spatial discretization scheme is necessary. Using a pseudo-spectral method based on finite Fourier series combined with an iterative scheme for the inversion of a non-local operator, the strongly nonlinear systems are solved numerically for the propagation of a single solitary wave and the head-on collision of two counter-propagating solitary waves of finite amplitudes, and the results are compared with previous laboratory measurements.

JFM classification

Waves/Free-surface Flows: Solitary waves Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 945 , 25 August 2022 , A15
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agnon, Y., Madsen, P.A. & Schäffer, H.A. 1999 A new approach to high-order Boussinesq models. J. Fluid Mech. 399, 319–333.CrossRefGoogle Scholar
Chen, Y. & Yeh, H. 2014 Laboratory experiments on counter-propagating collisions of solitary waves. Part 1. Wave interactions. J. Fluid Mech. 749, 577–596.CrossRefGoogle Scholar
Choi, W. 2019 On Rayleigh expansion for nonlinear long water waves. J. Hydrodyn. 31, 1115–1126.CrossRefGoogle Scholar
Choi, W., Barros, R. & Jo, T.-C. 2009 A regularized model for strongly nonlinear internal solitary waves. J. Fluid Mech. 629, 73–85.CrossRefGoogle Scholar
Choi, W. & Camassa, R. 1999 Fully nonlinear internal waves in a two-fluid system. J. Fluid Mech. 396, 1–36.CrossRefGoogle Scholar
Choi, W., Goullet, A. & Jo, T.-C. 2011 An iterative method to solve a regularized model for strongly nonlinear long internal waves. J. Comput. Phys. 230, 2021–2030.CrossRefGoogle Scholar
Craig, W. & Sulem, C. 1993 Numerical simulation of gravity waves. J. Comput. Phys. 108, 73–83.CrossRefGoogle Scholar
Dommermuth, D.G. & Yue, D.K.P. 1987 A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 184, 267–288.CrossRefGoogle Scholar
Fenton, J. 1972 A ninth-order solution for the solitary wave. J. Fluid Mech. 53, 257–271.CrossRefGoogle Scholar
Green, A.E. & Naghdi, P.M. 1976 Derivation of equations for wave propagation in water of variable depth. J. Fluid Mech. 78, 237–246.CrossRefGoogle Scholar
Grimshaw, R. 1971 The solitary wave in water of variable depth. Part 2. J. Fluid Mech. 46, 611–622.CrossRefGoogle Scholar
Kirby, J.T. 2020 A new instability for Boussinesq-type equations. J. Fluid Mech. 894, F1.CrossRefGoogle Scholar
Li, Y.A., Hyman, J.M. & Choi, W. 2004 A numerical study of the exact evolution equations for surface waves in water of finite depth. Stud. Appl. Maths 113, 303–324.CrossRefGoogle Scholar
Longuet-Higgins, M.S. & Fenton, J.D. 1974 On the mass, momentum, energy and circulation of a solitary wave. Proc. R. Soc. Lond. A 340, 471–493.Google Scholar
Madsen, P.A. & Agnon, Y. 2003 Accuracy and convergence of velocity formulations for water waves in the framework of Boussinesq theory. J. Fluid Mech. 477, 285–319.CrossRefGoogle Scholar
Madsen, P.A., Bingham, H.B. & Liu, H. 2002 A new approach to high-order Boussinesq models. J. Fluid Mech. 462, 1–30.CrossRefGoogle Scholar
Madsen, P.A. & Fuhrman, D.R. 2020 Trough instabilities in boussinesq formulations for water waves. J. Fluid Mech. 889, A38.CrossRefGoogle Scholar
Madsen, P.A. & Schäffer, H.A. 1998 Higher-order Boussinesq-type equations for surface gravity waves: derivation and analysis. Proc. R. Soc. Lond. A 356, 3123–3184.Google Scholar
Matsuno, Y. 2015 Hamiltonian formulation of the extended Green-Naghdi equations. Physica D 301–302, 1–7.CrossRefGoogle Scholar
Matsuno, Y. 2016 Hamiltonian structure for two-dimensional extended Green-Naghdi equations. Proc. R. Soc. A 472, 20160127.CrossRefGoogle Scholar
Mei, C.C. & Le Méhaute, B. 1966 Note on the equations of long waves over an uneven bottom. J. Geophys. Res. 71, 393–400.CrossRefGoogle Scholar
Miles, J.W. 1980 Solitary waves. Annu. Rev. Fluid Mech. 12, 11–43.CrossRefGoogle Scholar
Miyata, M. 1988 Long internal waves of large amplitude. In Proceedings of the IUTAM Symposium on Nonlinear Water Waves (ed. H. Horikawa & H. Maruo), pp. 399–406. Springer Verlag.CrossRefGoogle Scholar
Murashige, S. & Choi, W. 2015 High-order Davies’ approximation for a solitary wave solution in Packham's plane. SIAM J. Appl. Maths 75, 189–208.CrossRefGoogle Scholar
Nwogu, O. 1993 An alternative form of the Boussinesq equations for nearshore wave propagation. ASCE J. Waterway Port Coastal Ocean Engng 119, 618–638.CrossRefGoogle Scholar
Rayleigh, Lord 1876 On waves. J. W. S. Phil. Mag. 1, 257–279.Google Scholar
Serre, F. 1953 Contribution à l’étude des écoulements permanents et variables dans les canaux. La Houille Blanche 6, 830–872.CrossRefGoogle Scholar
Su, C.H. & Gardner, C.S. 1969 Korteweg-de Vries equation and generalizations. III: derivation of the Korteweg-de Vries equation and Burgers equation. J. Math. Phys. 10, 536–539.CrossRefGoogle Scholar
Tanaka, M. 1986 The stability of solitary waves. Phys. Fluids 29, 650–655.CrossRefGoogle Scholar
Tanaka, M., Dold, J.W., Lewy, M. & Peregrine, D.H. 1987 Instability and breaking of a solitary wave. J. Fluid Mech. 185, 235–248.CrossRefGoogle Scholar
Wei, G., Kirby, J.T., Grilli, S.T. & Subramanya, R. 1995 A fully nonlinear Boussinesq model for surface waves. Part I. Highly nonlinear unsteady waves. J. Fluid Mech. 294, 71–92.CrossRefGoogle Scholar
West, B.J., Brueckner, K.A., Janda, R.S., Milder, D.M. & Milton, R.L. 1987 A new numerical method for surface hydrodynamics. J. Geophys. Res. 92, 11803–11824.CrossRefGoogle Scholar
Whitham, G.B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar
Wu, T.Y. 1998 Nonlinear waves and solitons in water. Physica D 123, 48–63.CrossRefGoogle Scholar
Wu, T.Y. 1999 Modeling nonlinear dispersive water waves. J. Engng Mech. ASCE 11, 747–755.CrossRefGoogle Scholar
Zakharov, V.E. 1968 Stability of periodic waves of finite amplitude on the surface of deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194.CrossRefGoogle Scholar
Zhao, B.B., Ertekin, R.C., Duan, W.Y. & Hayatdavoodi, M. 2014 On the steady solitary-wave solution of the Green-Naghdi equations of different levels. Wave Motion 51, 1382–1395.CrossRefGoogle Scholar