Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Klymak, Jody M.
and
Legg, Sonya M.
2010.
A simple mixing scheme for models that resolve breaking internal waves.
Ocean Modelling,
Vol. 33,
Issue. 3-4,
p.
224.
Klymak, Jody M.
Legg, Sonya
and
Pinkel, Robert
2010.
A Simple Parameterization of Turbulent Tidal Mixing near Supercritical Topography.
Journal of Physical Oceanography,
Vol. 40,
Issue. 9,
p.
2059.
Xing, Jiuxing
and
Davies, Alan M.
2011.
On the interaction of internal tides over two adjacent sills in a fjord.
Journal of Geophysical Research,
Vol. 116,
Issue. C4,
Klymak, Jody M.
Alford, Matthew H.
Pinkel, Robert
Lien, Ren-Chieh
Yang, Yung Jang
and
Tang, Tswen-Yung
2011.
The Breaking and Scattering of the Internal Tide on a Continental Slope.
Journal of Physical Oceanography,
Vol. 41,
Issue. 5,
p.
926.
Eakin, Dan
Holbrook, W. S.
and
Fer, Ilker
2011.
Seismic reflection imaging of large-amplitude lee waves in the Caribbean Sea.
Geophysical Research Letters,
Vol. 38,
Issue. 21,
p.
n/a.
Sun, Oliver M.
and
Pinkel, Robert
2012.
Energy Transfer from High-Shear, Low-Frequency Internal Waves to High-Frequency Waves near Kaena Ridge, Hawaii.
Journal of Physical Oceanography,
Vol. 42,
Issue. 9,
p.
1524.
Pinkel, Robert
Rainville, Luc
and
Klymak, Jody
2012.
Semidiurnal Baroclinic Wave Momentum Fluxes at Kaena Ridge, Hawaii.
Journal of Physical Oceanography,
Vol. 42,
Issue. 8,
p.
1249.
Buijsman, Maarten C.
Legg, Sonya
and
Klymak, Jody
2012.
Double-Ridge Internal Tide Interference and Its Effect on Dissipation in Luzon Strait.
Journal of Physical Oceanography,
Vol. 42,
Issue. 8,
p.
1337.
Nash, Jonathan D.
Kelly, Samuel M.
Shroyer, Emily L.
Moum, James N.
and
Duda, Timothy F.
2012.
The Unpredictable Nature of Internal Tides on Continental Shelves.
Journal of Physical Oceanography,
Vol. 42,
Issue. 11,
p.
1981.
Klymak, Jody M.
Buijsman, Maarten
Legg, Sonya
and
Pinkel, Robert
2013.
Parameterizing Surface and Internal Tide Scattering and Breaking on Supercritical Topography: The One- and Two-Ridge Cases.
Journal of Physical Oceanography,
Vol. 43,
Issue. 7,
p.
1380.
Itoh, Sachihiko
Tanaka, Yuki
Osafune, Satoshi
Yasuda, Ichiro
Yagi, Masahiro
Kaneko, Hitoshi
Konda, Shunsuke
Nishioka, Jun
and
N. Volkov, Yuri.
2014.
Direct breaking of large-amplitude internal waves in the Urup Strait.
Progress in Oceanography,
Vol. 126,
Issue. ,
p.
109.
Warner, Sally J.
and
MacCready, Parker
2014.
The dynamics of pressure and form drag on a sloping headland: Internal waves versus eddies.
Journal of Geophysical Research: Oceans,
Vol. 119,
Issue. 3,
p.
1554.
Buijsman, Maarten C.
Klymak, Jody M.
Legg, Sonya
Alford, Matthew H.
Farmer, David
MacKinnon, Jennifer A.
Nash, Jonathan D.
Park, Jae-Hun
Pickering, Andy
and
Simmons, Harper
2014.
Three-Dimensional Double-Ridge Internal Tide Resonance in Luzon Strait.
Journal of Physical Oceanography,
Vol. 44,
Issue. 3,
p.
850.
Gregg, M. C.
and
Klymak, Jody M.
2014.
Mode-2 hydraulic control of flow over a small ridge on a continental shelf.
Journal of Geophysical Research: Oceans,
Vol. 119,
Issue. 11,
p.
8093.
Alford, Matthew H.
Klymak, Jody M.
and
Carter, Glenn S.
2014.
Breaking internal lee waves at Kaena Ridge, Hawaii.
Geophysical Research Letters,
Vol. 41,
Issue. 3,
p.
906.
da Silva, J.C.B.
Buijsman, M.C.
and
Magalhaes, J.M.
2015.
Internal waves on the upstream side of a large sill of the Mascarene Ridge: a comprehensive view of their generation mechanisms and evolution.
Deep Sea Research Part I: Oceanographic Research Papers,
Vol. 99,
Issue. ,
p.
87.
Dale, Andrew C.
and
Inall, Mark E.
2015.
Tidal mixing processes amid small‐scale, deep‐ocean topography.
Geophysical Research Letters,
Vol. 42,
Issue. 2,
p.
484.
Bogoni, Manuel
Canestrelli, Alberto
and
Lanzoni, Stefano
2015.
Finite volume modelling of a stratified flow with the presence of submerged weirs.
Journal of Applied Water Engineering and Research,
Vol. 3,
Issue. 1,
p.
43.
Gemmrich, Johannes
and
Klymak, Jody M.
2015.
Dissipation of Internal Wave Energy Generated on a Critical Slope.
Journal of Physical Oceanography,
Vol. 45,
Issue. 9,
p.
2221.
Jiang‐Xin, CHEN
Yang, BAI
Yong‐Xian, GUAN
Sheng‐Xiong, YANG
Hai‐Bin, SONG
and
Bo‐Ran, LIU
2016.
GEOPHYSICAL ANALYSIS OF ABNORMAL SEISMIC (OCEANOGRAPHY) REFLECTION CHARACTERISTICS OF OCEANIC BOTTOM BOUNDARY LAYER.
Chinese Journal of Geophysics,
Vol. 59,
Issue. 5,
p.
573.
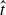 = tNα/2π for the growth of the lee waves, and that steady state is attained more rapidly with steep topography than shallow, in contrast with linear theory, which does not depend on the aspect ratio.
= tNα/2π for the growth of the lee waves, and that steady state is attained more rapidly with steep topography than shallow, in contrast with linear theory, which does not depend on the aspect ratio.