Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T15:22:57.260Z Has data issue: false hasContentIssue false
  • English
  • Français

High-frequency viscosity of a dilute suspension of elongated particles in a linear shear flow between two walls

Published online by Cambridge University Press:  23 December 2014

François Feuillebois ,
Maria L. Ekiel-Jeżewska ,
Eligiusz Wajnryb ,
Antoine Sellier  and
Jerzy Bławzdziewicz
François Feuillebois*
Affiliation:
LIMSI-CNRS, UPR 3251, Rue John von Neumann Campus Universitaire d’Orsay Bât 508, 91405 Orsay CEDEX, France
Maria L. Ekiel-Jeżewska
Affiliation:
Institute of Fundamental Technological Research, Polish Academy of Sciences, Pawińskiego 5b, 02-106 Warsaw, Poland
Eligiusz Wajnryb
Affiliation:
Institute of Fundamental Technological Research, Polish Academy of Sciences, Pawińskiego 5b, 02-106 Warsaw, Poland
Antoine Sellier
Affiliation:
LadHyX, École Polytechnique, 91128 Palaiseau CEDEX, France
Jerzy Bławzdziewicz
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A general expression for the effective viscosity of a dilute suspension of arbitrary-shaped particles in linear shear flow between two parallel walls is derived in terms of the induced stresslets on particles. This formula is applied to 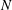$N$-bead rods and to prolate spheroids with the same length, aspect ratio and volume. The effective viscosity of non-Brownian particles in a periodic shear flow is considered here. The oscillating frequency is high enough for the particle orientation and centre-of-mass distribution to be practically frozen, yet small enough for the flow to be quasi-steady. It is known that for spheres, the intrinsic viscosity 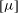$[{\it\mu}]$ increases monotonically when the distance 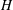$H$ between the walls is decreased. The dependence is more complex for both types of elongated particles. Three regimes are theoretically predicted here: (i) a ‘weakly confined’ regime (for 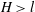$H>l$, where 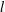$l$ is the particle length), where 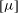$[{\it\mu}]$ is slightly larger for smaller 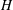$H$; (ii) a ‘semi-confined’ regime, when 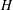$H$ becomes smaller than 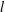$l$, where 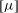$[{\it\mu}]$ rapidly decreases since the geometric constraints eliminate particle orientations corresponding to the largest stresslets; (iii) a ‘strongly confined’ regime when 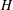$H$ becomes smaller than 2–3 particle widths 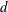$d$, where 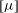$[{\it\mu}]$ rapidly increases owing to the strong hydrodynamic coupling with the walls. In addition, for sufficiently slender particles (with aspect ratio larger than 5–6) there is a domain of narrow gaps for which the intrinsic viscosity is smaller than that in unbounded fluid.

JFM classification

Complex Fluids: Complex Fluids Low-Reynolds-number flows: Low-Reynolds-number flows Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 764 , 10 February 2015 , pp. 133 - 147
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhattacharya, S., Bławzdziewicz, J. & Wajnryb, E. 2005a Hydrodynamic interactions of spherical particles in suspensions confined between two planar walls. J. Fluid Mech. 541, 263–292.Google Scholar
Bhattacharya, S., Bławzdziewicz, J. & Wajnryb, E. 2005b Many-particle hydrodynamic interactions in parallel-wall geometry: Cartesian-representation method. Physica A 356, 294–340.Google Scholar
Brenner, H. 1974 Rheology of a dilute suspension of axisymmetric Brownian particles. J. Multiphase Flow 1, 195–341.Google Scholar
Bretherton, F. P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14, 284–304.Google Scholar
Brunn, P. 1981 The hydrodynamic wall effect for a disperse system. Intl J. Multiphase Flow 7, 221–234.CrossRefGoogle Scholar
Davit, Y. & Peyla, P. 2008 Intriguing viscosity effects in confined suspensions: a numerical study. Europhys. Lett. 83, 64001.CrossRefGoogle Scholar
Einstein, A. 1906 Eine neue Bestimmung der Molekuldimensionen. Ann. Phys. 19, 289–306.CrossRefGoogle Scholar
Einstein, A. 1911 Berichtung zu meiner Arbeit: Eine neue Bestimmung der Molekuldimensionen. Ann. Phys. 34, 591–592.Google Scholar
Ekiel-Jeżewska, M. L. & Wajnryb, E. 2009 Precise multipole method for calculating hydrodynamic interactions between spherical particles in the Stokes flow. In Theoretical Methods for Micro Scale Viscous Flows (ed. Feuillebois, F. & Sellier, A.), pp. 127–172. Transworld Research Network, ISBN: 978-81-7895-400-4.Google Scholar
Ekiel-Jeżewska, M. L., Wajnryb, E., Bławzdziewicz, J. & Feuillebois, F. 2008 Lubrication approximation for microparticles moving along parallel walls. J. Chem. Phys. 129, 18102.Google Scholar
Feuillebois, F., Lecoq, N. & Pasol, L. 2007 Effective hydrodynamic flow of suspensions in presence of apparent slip at boundaries. In CP946, Applications of Mathematics in Engineering and Economics’33, 33rd International Conference (ed. Todorov, M. D.), pp. 23–34. American Institute of Physics.Google Scholar
Happel, J. & Brenner, H. 1973 Low Reynolds Number Hydrodynamics. Noordhoff.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Jones, R. B. 2004 Spherical particle in Poiseuille flow between planar walls. J. Chem. Phys. 121 (1), 483–500.Google Scholar
Liron, N. & Mochon, S. 1976 Stokes flow for a stokeslet between two parallel flat plates. J. Engng Maths 10 (4), 287–303.Google Scholar
Park, J. & Butler, J. A. 2009 Inhomogeneous distribution of a rigid fibre undergoing rectilinear flow between parallel walls at high Péclet numbers. J. Fluid Mech. 630, 267–298.Google Scholar
Pasol, L.2003 Interactions hydrodynamiques dans les suspensions. Effets collectifs. PhD thesis, Université Pierre et Marie Curie, Paris VI.Google Scholar
Pasol, L. & Sellier, A. 2006 Sedimentation of a solid particle in a fluid. Comput. Model. Eng. Sci. 16 (3), 187–196.Google Scholar
Peyla, P. & Verdier, C. 2011 New confinement effects on the viscosity of suspensions. Europhys. Lett. 94, 44001.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Sangani, A. S., Acrivos, A. & Peyla, P. 2011 Roles of particle–wall and particle–particle interactions in highly confined suspensions of spherical particles being sheared at low Reynolds numbers. Phys. Fluids 23, 083302.Google Scholar
Sheraga, H. A. 1955 Non-Newtonian viscosity of solutions of ellipsoidal particles. J. Chem. Phys. 23 (8), 1526–1532.CrossRefGoogle Scholar
Shikata, T. & Pearson, D. S. 1994 Viscoelastic behavior of concentrated spherical suspensions. J. Rheol. 38, 601–616.Google Scholar
Swan, J. W. & Brady, J. F. 2010 Particle motion between parallel walls: hydrodynamics and simulation. Phys. Fluids 22, 103301.Google Scholar
Tozeren, H. & Skalak, R. 1983 Stress in a suspension near rigid boundaries. J. Fluid Mech. 82, 289–307.Google Scholar
Van der Werff, J. C., De Kruif, C. G., Blom, C. & Mellema, J. 1989 Linear viscoelastic behavior of dense hard-sphere dispersions. Phys. Rev. A 39, 795–807.CrossRefGoogle Scholar
Zurita-Gotor, M., Bławzdziewicz, J. & Wajnryb, E. 2007 Motion of a rod-like particle between parallel walls with application to suspension rheology. J. Rheol. 51, 71–97.Google Scholar