Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-09T22:03:02.825Z Has data issue: false hasContentIssue false
  • English
  • Français

High-enthalpy flow over a rearward-facing step – a computational study

Published online by Cambridge University Press:  20 February 2012

N. R. Deepak ,
S. L. Gai  and
A. J. Neely
N. R. Deepak*
Affiliation:
School of Engineering & Information Technology, University of New South Wales, Australian Defence Force Academy, Canberra ACT 2600, Australia
S. L. Gai
Affiliation:
School of Engineering & Information Technology, University of New South Wales, Australian Defence Force Academy, Canberra ACT 2600, Australia
A. J. Neely
Affiliation:
School of Engineering & Information Technology, University of New South Wales, Australian Defence Force Academy, Canberra ACT 2600, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

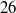Hypersonic, high-enthalpy flow over a rearward-facing step has been numerically investigated using computational fluid dynamics (CFD). Two conditions relevant to suborbital and superorbital flow with total specific enthalpies of and 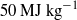, are considered. The Mach number and unit Reynolds number per metre were 7.6, 11.0 and 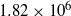, 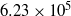respectively. The Reynolds number based on the step height was correspondingly 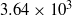and . The computations were carried out assuming the flow to be laminar throughout and the real gas effects such as thermal and chemical non-equilibrium are studied using Park’s two-temperature model with finite-rate chemistry and Gupta’s finite-rate chemistry models. In the close vicinity of the step, detailed quantification of flow features is emphasised. In particular, the presence of the Goldstein singularity at the lip and separation on the face of the step have been elucidated. Within the separated region and downstream of reattachment, the influence of real gas effects has been identified and shown to be negligible. The numerical results are compared with the available experimental data of surface heat flux downstream of the step and reasonable agreement is shown up to 30 step heights downstream.

JFM classification

Boundary Layers: Boundary layer separation Compressible Flows: Gas dynamics Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 695 , 25 March 2012 , pp. 405 - 438
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. AIAA, 1994 Policy statement on numerical accuracy and experimental uncertainty. AIAA J. 32 (1)3 (editorial).Google Scholar
2. Ait-Ali-Yahia, D. 1996 A finite element segregated method for thermo-chemical equilibrium and non-equilibrium hypersonic flows using adapted grids. PhD thesis, Concordia University.CrossRefGoogle Scholar
3. van Albada, G. D., Leer, B. V. & Roberts, W. W. 1982 A comparative study of computational methods in cosmic gas dynamics. Astron. Astrophys. 108 (1), 76–84.Google Scholar
4. Allen, J. S. & Cheng, S. I. 1970 Numerical solution of the compressible Navier–Stokes equations for the laminar near wake. Phys. Fluids 13 (1), 37–51.Google Scholar
5. Anderson, W. K. & Thomas, J. L. 1986 A comparison of finite volume flux vector splittings for the euler equations. AIAA J. 24 (9), 1453–1460.Google Scholar
6. Baker, P. J. & Martin, W. 1966 Heat transfer in supersonic separated flow over a two-dimensional backward-facing step. Intl J. Heat Mass Transfer 9 (10), 1081–1088.Google Scholar
7. Bertin, J. J. & Cummings, R. M. 2003 Fifty years of hypersonics: where we’ve been, where we’re going. Prog. Aeronaut. Sci. 39 (6–7), 511–536.Google Scholar
8. Bertin, J. J. & Cummings, R. M. 2006 Critical hypersonic aerothermodynamic phenomena. Annu. Rev. Fluid Mech. 38, 129–157.Google Scholar
9. Borovoi, V. Ya, Skuratov, A. K. & Yegorov, L. V. 1998 Aerothermal study of martian probe. In Proceedings of the Third European Symposium on Aerothermodynamics for Space Vehicles, 24–26th November 1998, ESTEC, Noordwijk, The Netherlands, ESA SP-426.Google Scholar
10. Chen, Y.-K., Henline, W. D., Stewart, D. A. & Candler, G. V. 1993 Navier–Stokes solutions with surface catalysis for martian atmospheric entry. J. Spacecr. Rockets 30 (1), 32–42.Google Scholar
11. Corda, S. 1982 Numerical investigation of the laminar, supersonic flow over a rearward-facing step using an adaptive grid scheme. Master’s thesis, Department of Aerospace Eningeering, University of Maryland.Google Scholar
12. Deepak, N. R. 2010 Computational studies of hypersonic high enthalpy separated flows. PhD thesis, School of Engineering and Information Technology, University of New South Wales, Australian Defence Force Academy.Google Scholar
13. Deepak, N. R., Gai, S. L. & Neely, A. J. 2010 a A computational study of high enthalpy flow over a rearward facing step. In 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition in Orlando, Florida, 4–7 Jan. 2010. AIAA 2010-444.Google Scholar
14. Deepak, N. R., Gai, S. L. & Neely, A. J. 2010b Investigation of heat-flux in high enthalpy hypersonic flow over a rearward-facing step. Intl J. Hypersonics 1 (2), 115–134.Google Scholar
15. Dewey, C. F. 1965 A correlation of convective heat transfer and recovery temperature data for cylinders in compressible flow. Intl J. Heat Mass Transfer 8, 245–252.Google Scholar
16. Donaldson, I. S. 1967 On the separation of a supersonic flow at a sharp corner. AIAA J. 5 (6), 1086–1088.Google Scholar
17. Druguet, M.-C., Ben-Dor, G. & Zeitoun, D. 2007 The interaction of supersonic and hypersonic flows with a double cone: comparison between inviscid, viscous, perfect and real gas model simulations. In 26th International Symposium on Shock Waves, Gottingen, Germany, vol. 2.Google Scholar
18. Druguet, M.-C., Candler, G. V. & Nompelis, I. 2005 Effects of numerics on Navier–Stokes computations of hypersonic double-cone flows. AIAA J. 43 (3), 616–623.Google Scholar
19. Gai, S. L. 1992 Separated high enthalpy dissociated laminar hypersonic flow behind a step-pressure measurements. AIAA J. 30 (7), 1915–1918.CrossRefGoogle Scholar
20. Gai, S. L., Hayne, M. J., Gardner, A. D., Morgan, R. G. & Mee, D. J. 2001 Heat transfer behind a step in high enthalpy super-orbital flow. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, 8–11 Jan. 2001, Reno, Nevada. AIAA 2001-509.Google Scholar
21. Gai, S. L. & Milthorpe, J. F 1995 Hypersonic high-enthalpy flow over a blunt-stepped cone. In 20th International Symposium on Shock Waves, Pasadena, California, 23–28 July 1995.Google Scholar
22. Gai, S. L., Reynolds, N. T., Ross, C. & Baird, J. P. 1989 Measurements of heat transfer in separated high-enthalpy dissociated laminar hypersonic flow behind a step. J. Fluid Mech. 199, 541–561.CrossRefGoogle Scholar
23. Gnoffo, P. A. 2001 CFD validation studies for hypersonic flow prediction. In 39th AIAA Aerospace Sciences Meeting & Exhibit, 8–11 Jan. 2001, Reno, Nevada. AIAA 2001-1025.Google Scholar
24. Goldstein, S. 1946 On laminar boundary-layer flow near a position of separation. Q. J. Mech. Appl. Maths 1, 43–69.Google Scholar
25. Gollan, R. J. 2008 The computational modelling of high-temperature gas effects with application to hypersonic flows. PhD thesis, Department of Mechanical Engineering, University of Queensland.Google Scholar
26. Gordon, S. & McBride, B. J. 1994 Computer program for calculation of complex chemical equilibrium compositions and applications. I. Analysis. NASA Tech. Rep., Reference Publication 1311.Google Scholar
27. Gorshkov, A. B. & Lunev, V. V. 2002 Laminar base flow downstream of slender cones in hypersonic flow. Fluid Dyn. 37 (5), 772–783.Google Scholar
28. Grasso, F. & Pettinelli, C. 1995 Analysis of laminar near-wake hypersonic flows. J. Spacecr. Rockets 32 (6), 970–980.Google Scholar
29. Grotowsky, I. M. G. & Ballmann, J. 2000 Numerical investigation of hypersonic step-flows. Shock Waves 10 (1), 57–72.CrossRefGoogle Scholar
30. Gupta, R. N., Yos, J. M., Thompson, R. A. & Lee, K.-P. 1990 A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal non-equilibrium calculations to 30000 K. NASA Tech. Rep. 1232.Google Scholar
31. Hama, F. R. 1966 Experimental investigations of wedge base pressure and lip shock. Tech. Rep. N67 14905. Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California.Google Scholar
32. Hama, F. R. 1968 Experimental studies on the lip shock. AIAA J. 6 (2), 212–219.Google Scholar
33. Harvey, J. K., Holden, M. S. & Wadhams, T. P. 2001 Code validation study of laminar shock/boundary layer and shock/shock interactions in hypersonic flow. Part b. Comparison with Navier–Stokes and DSMC solutions. In Aerospace Sciences Meeting and Exhibit, 39th, Reno, Nevada, Jan. 8–11, 2001.Google Scholar
34. Hayne, M. J. 2004 Hypervelocity flow over rearward-facing steps. PhD thesis, Department of Mechanical Engineering, University of Queensland.Google Scholar
35. Hayne, M. J., Gai, S. L., Hillier, R., Morgan, R. G., Mee, D. J. & McIntyre, T. J. 2002 Heat transfer and flow behind a rearward facing step in a super-orbital expansion tube. In 23rd International Symposium on Shock Waves, 22–27 July 2002 Fort Worth, Texas, USA (ed. F. K. Lu), pp. 1574–1580.Google Scholar
36. Hayne, M. J., Gai, S. L., Mee, D. J. & Morgan, R. G. 2004 Real gas effects on flows over rearward-facing steps. In Proceedings of 24th International Symposium on Shock Waves, Beijing, China, pp. 251–256.Google Scholar
37. Hayne, M. J., Mee, D. J., Morgan, R. G., Gai, S. L. & McIntyre, T. J. 2003 Heat transfer and flow behind a step in high enthalpy superorbital flow. Aeronaut. J. 107 (2778), 435–442.Google Scholar
38. Holden, M. S. 1971 Establishment time of laminar separated flows. AIAA J. 9 (11), 2296–2298.CrossRefGoogle Scholar
39. Hollis, B. R. & Perkins, J. N. 1999 Transition effects on heating in the wake of a blunt body. J. Spacecr. Rockets 36 (5), 668–674.Google Scholar
40. Jackson, A. P., Hillier, R. & Soltani, S. 2001 Experimental and computational study of laminar cavity flows at hypersonic speeds. J. Fluid Mech. 427, 329–358.Google Scholar
41. Jacobs, P. A. 1991 Single-block Navier–Stokes integrator. Tech. Rep. ICASE Interim Report 18. NASA Langley Research Center, Hampton, VA.Google Scholar
42. Jacobs, P. A. 1996 MB-CNS: a computer program for the simulation of transient compressible flows. Tech. Rep. 10/96. Department of Mechanical Engineering, University of Queensland.Google Scholar
43. Jacobs, P. A. & Gollan, R. J. 2010 The Eilmer3 code. Tech. Rep. 2008/07. Department of Mechanical Engineering, University of Queensland.Google Scholar
44. Jacobs, P. A., Gollan, R. J., Denman, A. F., O’Flaherty, B. T., Potter, D. F., Petrie-Repar, P. J. & Johnston, I. A. 2010 Eilmer’s theory book: basic models for gas dynamics and thermochemistry. Tech. Rep. 2010/09. Department of Mechanical Engineering, University of Queensland, Brisbane.Google Scholar
45. Jakubowski, A. K. & Lewis, C. H. 1974 Rearward-facing steps in laminar supersonic flows with and without suction. NASA Tech. Rep. NASA-CR-132476.Google Scholar
46. Khan, O. U. & Hoffmann, K. A. 2010 Unsteady supersonic flows over a backward-facing step with applied magnetic field. J. Spacecr. Rockets 47 (3), 405–412.Google Scholar
47. Kuruvila, G. & Anderson, J. D. 1985 A study of the effects of numerical dissipation on the calculation of supersonic separated flow. In 23rd AIAA Aerospace Sciences Meeting, January 14–17, 1985, Reno, Nevada. AIAA 85-0301.Google Scholar
48. Leer, B. V. 1979 Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 32, 101–136.Google Scholar
49. Leite, P. H. M. & Santos, W. F. N. 2009 Direct simulation calculations of the rarefied hypersonic flow past a backward-facing step. In 3rd CTA-DLR Workshop on Data Analysis & Flight Control, Brazilian Symposium on Aerospace Engineering & Applications.Google Scholar
50. McBride, B. J. & Gordon, S. 1996 Computer program for calculation of complex chemical equilibrium compositions and applications. II. User manual and program description. NASA Tech. Rep. Reference Publ. 1311.Google Scholar
51. Millikan, R. C. & White, D. R. 1963 Systematics of vibrational relaxation. J. Chem. Phys. 39 (12), 3209–3213.CrossRefGoogle Scholar
52. Mott, D. R. 1999 New quasi-steady-state and partial-equilibrium methods for integrating chemically reacting systems. PhD thesis, The University of Michigan.Google Scholar
53. Paciorri, R., Sabetta, F. & Favini, B. 1998 On the role of vibrational excitation in hypersonic flow computations. Meccanica 33 (4), 331–347.CrossRefGoogle Scholar
54. Papadopoulos, P., Venkatapathy, E., Prabhu, D. & Loomis, M. P. 1999 Current grid-generation strategies and future requirements in hypersonic vehicle design, analysis and testing. Appl. Math. Model. 23 (9), 705–735.CrossRefGoogle Scholar
55. Park, C. 1993 Review of chemical-kinetic problems of future NASA missions. I. Earth entries. J. Thermophys. Heat Transfer 7 (3), 385–398.CrossRefGoogle Scholar
56. Park, G., Gai, S. L. & Neely, A. J. 2010 Aerothermodynamics behind a blunt body at superorbital speeds. AIAA J. 48 (8), 1804–1816.Google Scholar
57. Priolo, F. J. 1983 The effect of grid compression on the accuracy of numerical solutions for laminar supersonic flow over a rearward facing step. Master’s thesis, Department of Aerospace Eningeering, University of Maryland.Google Scholar
58. Roache, P. J. 1997 Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 29, 123–160.Google Scholar
59. Roache, P. J, Ghia, K. N. & White, F. M. 1986 Editorial policy statement on the control of numerical accuracy. Trans. ASME: J. Fluids Engng 108, 2.Google Scholar
60. Roache, P. J & Mueller, T. J. 1968 Numerical solutions of compressible and incompressible laminar separated flows. In AIAA Fluid and Plasma Dynamics Conference, Los Angeles, California, June 24–26, 1968. AIAA 1968-741.Google Scholar
61. Rom, J. & Seginer, A. 1964 Laminar heat transfer to a two-dimensional backward facing step from the high-enthalpy supersonic flow in the shock tube. AIAA J. 2 (2), 251–255.CrossRefGoogle Scholar
62. Ross, B. B. & Cheng, S. I. 1971 A numerical solution of the planar supersonic near-wake with its error analysis. In Proceedings of the Second International Conference on Numerical Methods in Fluid Dynamics, Lecture Notes in Physics , vol. 8/1971. pp. 164–169.CrossRefGoogle Scholar
63. Ruffin, S. M. & Park, C. 1993 Vibrational relaxation of anharmonic oscillators in expanding flows. J. Spacecr. Rockets 30 (1), 59–68.CrossRefGoogle Scholar
64. Sandford, J. & Ginoux, J. J. 1968 Laminar, transitional and turbulent heat transfer behind a backward facing step in supersonic flow. Tech. Rep. 38, Von Karman Institute for Fluid Dynamics.Google Scholar
65. Scherberg, M. G. & Smith, H. E. 1967 An experimental study of supersonic flow over a rearward facing step. AIAA J. 5 (1), 51–56.CrossRefGoogle Scholar
66. Stewartson, K. 1968 On the flow near the trailing edge of a flat plate. Proc. R. Soc. A 306 (1486), 275–290.Google Scholar
67. Tchuen, G. & Zeitoun, D. E. 2009 Effects of chemistry in non-equilibrium hypersonic flow around blunt bodies. J. Thermophys. Heat Transfer 23 (3), 433–442.CrossRefGoogle Scholar
68. Tecplot, 2009 Tecplot 360, 2009, Tecplot, Inc. (formerly Amtec Engineering, Inc.) 3535 Factoria Blvd S.E. Suite 550 Bellevue, WA 98006.Google Scholar
69. Wada, I. & Inoue, Y. 1973 Heat transfer behind a backward facing step. Heat Transfer Japan. Res. 2 (2), 39–42.Google Scholar
70. Wada, Y. & Liou, M. S. 1994 A flux splitting scheme with high-resolution and robustness for discontinuities. In Aerospace Sciences Meeting and Exhibit, 32nd, Reno, Nevada, Jan. 10–13, 1994. AIAA 1994-83.Google Scholar
71. Weinbaum, S. 1966 Specialist meeting on separated flows. In AGARD Conference Proceedings 4. Brussels.Google Scholar
72. Weinbaum, S. 1968 On the singular points in the laminar two-dimensional near wake flow field. J. Fluid Mech. 33 (1), 39–63.Google Scholar
73. Wilke, C. R. 1950 A viscosity equation for gas mixtures. J. Chem. Phys. 18 (4), 517–519.Google Scholar