Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Herbert, Corentin
Marino, Raffaele
Rosenberg, Duane
and
Pouquet, Annick
2016.
Waves and vortices in the inverse cascade regime of stratified turbulence with or without rotation.
Journal of Fluid Mechanics,
Vol. 806,
Issue. ,
p.
165.
Bierdel, Lotte
Snyder, Chris
Park, Sang-Hun
and
Skamarock, William C.
2016.
Accuracy of Rotational and Divergent Kinetic Energy Spectra Diagnosed from Flight-Track Winds.
Journal of the Atmospheric Sciences,
Vol. 73,
Issue. 8,
p.
3273.
LaCasce, J.
2016.
Estimating Eulerian Energy Spectra from Drifters.
Fluids,
Vol. 1,
Issue. 4,
p.
33.
Balwada, Dhruv
LaCasce, Joseph H.
and
Speer, Kevin G.
2016.
Scale‐dependent distribution of kinetic energy from surface drifters in the Gulf of Mexico.
Geophysical Research Letters,
Vol. 43,
Issue. 20,
Durran, Dale R.
and
Weyn, Jonathan A.
2016.
Thunderstorms Do Not Get Butterflies.
Bulletin of the American Meteorological Society,
Vol. 97,
Issue. 2,
p.
237.
Callies, Jörn
Bühler, Oliver
and
Ferrari, Raffaele
2016.
The Dynamics of Mesoscale Winds in the Upper Troposphere and Lower Stratosphere.
Journal of the Atmospheric Sciences,
Vol. 73,
Issue. 12,
p.
4853.
Hewer, Rüdiger
Friederichs, Petra
Hense, Andreas
and
Schlather, Martin
2017.
A Matérn-Based Multivariate Gaussian Random Process for a Consistent Model of the Horizontal Wind Components and Related Variables.
Journal of the Atmospheric Sciences,
Vol. 74,
Issue. 11,
p.
3833.
Lindborg, Erik
and
Mohanan, Ashwin Vishnu
2017.
A two-dimensional toy model for geophysical turbulence.
Physics of Fluids,
Vol. 29,
Issue. 11,
Bühler, Oliver
Kuang, Max
and
Tabak, Esteban G.
2017.
Anisotropic Helmholtz and wave–vortex decomposition of one-dimensional spectra.
Journal of Fluid Mechanics,
Vol. 815,
Issue. ,
p.
361.
Flores, Oscar
Riley, James J.
and
Horner-Devine, Alexander R.
2017.
On the dynamics of turbulence near a free surface.
Journal of Fluid Mechanics,
Vol. 821,
Issue. ,
p.
248.
Achatz, U.
Ribstein, B.
Senf, F.
and
Klein, R.
2017.
The interaction between synoptic‐scale balanced flow and a finite‐amplitude mesoscale wave field throughout all atmospheric layers: weak and moderately strong stratification.
Quarterly Journal of the Royal Meteorological Society,
Vol. 143,
Issue. 702,
p.
342.
Sun, Y. Qiang
Rotunno, Richard
and
Zhang, Fuqing
2017.
Contributions of Moist Convection and Internal Gravity Waves to Building the Atmospheric −5/3 Kinetic Energy Spectra.
Journal of the Atmospheric Sciences,
Vol. 74,
Issue. 1,
p.
185.
Poje, Andrew C.
Özgökmen, Tamay M.
Bogucki, Darek J.
and
Kirwan, A. D.
2017.
Evidence of a forward energy cascade and Kolmogorov self-similarity in submesoscale ocean surface drifter observations.
Physics of Fluids,
Vol. 29,
Issue. 2,
Soh, Hyun Sup
and
Kim, Sung Yong
2018.
Diagnostic Characteristics of Submesoscale Coastal Surface Currents.
Journal of Geophysical Research: Oceans,
Vol. 123,
Issue. 3,
p.
1838.
Li, Qiang
and
Lindborg, Erik
2018.
Weakly or Strongly Nonlinear Mesoscale Dynamics Close to the Tropopause?.
Journal of the Atmospheric Sciences,
Vol. 75,
Issue. 4,
p.
1215.
Asselin, Olivier
Bartello, Peter
and
Straub, David N.
2018.
On Boussinesq Dynamics near the Tropopause.
Journal of the Atmospheric Sciences,
Vol. 75,
Issue. 2,
p.
571.
Kafiabad, Hossein A.
and
Bartello, Peter
2018.
Spontaneous imbalance in the non-hydrostatic Boussinesq equations.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
614.
Chunchuzov, Igor
2018.
Nonlinear Formation of the Three-Dimensional Spectrum of Mesoscale Wind Velocity and Temperature Fluctuations in a Stably Stratified Atmosphere.
Journal of the Atmospheric Sciences,
Vol. 75,
Issue. 10,
p.
3447.
Choi, J.
Park, Y.‐G.
Kim, W.
and
Kim, Y. H.
2019.
Characterization of Submesoscale Turbulence in the East/Japan Sea Using Geostationary Ocean Color Satellite Images.
Geophysical Research Letters,
Vol. 46,
Issue. 14,
p.
8214.
Won, Sang In
Kim, Sung Yong
and
Kim, Kyeong Ok
2019.
Submesoscale Surface Tidal, Vortical, and Residual Circulations in a Semienclosed Bay.
Journal of Geophysical Research: Oceans,
Vol. 124,
Issue. 7,
p.
5105.
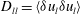 $D_{ll}=\langle {\it\delta}u_{l}{\it\delta}u_{l}\rangle$ and
$D_{ll}=\langle {\it\delta}u_{l}{\it\delta}u_{l}\rangle$ and  $D_{tt}=\langle {\it\delta}u_{t}{\it\delta}u_{t}\rangle$, can be calculated from aircraft data. Here,
$D_{tt}=\langle {\it\delta}u_{t}{\it\delta}u_{t}\rangle$, can be calculated from aircraft data. Here, 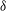 ${\it\delta}$ denotes the increment between two points separated by a distance
${\it\delta}$ denotes the increment between two points separated by a distance  $r$,
$r$, 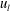 $u_{l}$ and
$u_{l}$ and 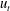 $u_{t}$ the velocity components parallel and perpendicular to the aircraft track respectively and
$u_{t}$ the velocity components parallel and perpendicular to the aircraft track respectively and 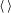 $\langle \,\rangle$ an average. Assuming statistical axisymmetry and making a Helmholtz decomposition of the horizontal velocity,
$\langle \,\rangle$ an average. Assuming statistical axisymmetry and making a Helmholtz decomposition of the horizontal velocity, 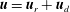 $\boldsymbol{u}=\boldsymbol{u}_{r}+\boldsymbol{u}_{d}$, where
$\boldsymbol{u}=\boldsymbol{u}_{r}+\boldsymbol{u}_{d}$, where 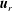 $\boldsymbol{u}_{r}$ is the rotational and
$\boldsymbol{u}_{r}$ is the rotational and 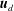 $\boldsymbol{u}_{d}$ the divergent component of the velocity, we derive expressions relating the structure functions
$\boldsymbol{u}_{d}$ the divergent component of the velocity, we derive expressions relating the structure functions 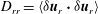 $D_{rr}=\langle {\it\delta}\boldsymbol{u}_{r}\boldsymbol{\cdot }{\it\delta}\boldsymbol{u}_{r}\rangle$ and
$D_{rr}=\langle {\it\delta}\boldsymbol{u}_{r}\boldsymbol{\cdot }{\it\delta}\boldsymbol{u}_{r}\rangle$ and 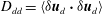 $D_{dd}=\langle {\it\delta}\boldsymbol{u}_{d}\boldsymbol{\cdot }{\it\delta}\boldsymbol{u}_{d}\rangle$ to
$D_{dd}=\langle {\it\delta}\boldsymbol{u}_{d}\boldsymbol{\cdot }{\it\delta}\boldsymbol{u}_{d}\rangle$ to 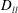 $D_{ll}$ and
$D_{ll}$ and 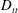 $D_{tt}$. Corresponding expressions are also derived in spectral space. The decomposition is applied to structure functions calculated from aircraft data. In the lower stratosphere,
$D_{tt}$. Corresponding expressions are also derived in spectral space. The decomposition is applied to structure functions calculated from aircraft data. In the lower stratosphere,  $D_{rr}$ and
$D_{rr}$ and 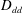 $D_{dd}$ both show a nice
$D_{dd}$ both show a nice 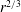 $r^{2/3}$-dependence for
$r^{2/3}$-dependence for 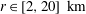 $r\in [2,20]\ \text{km}$. In this range, the ratio between rotational and divergent energy is a little larger than unity, excluding gravity waves as the principal agent behind the observations. In the upper troposphere,
$r\in [2,20]\ \text{km}$. In this range, the ratio between rotational and divergent energy is a little larger than unity, excluding gravity waves as the principal agent behind the observations. In the upper troposphere, 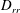 $D_{rr}$ and
$D_{rr}$ and 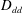 $D_{dd}$ show no clean
$D_{dd}$ show no clean 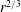 $r^{2/3}$-dependence, although the overall slope of
$r^{2/3}$-dependence, although the overall slope of 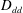 $D_{dd}$ is close to
$D_{dd}$ is close to 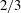 $2/3$ for
$2/3$ for 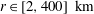 $r\in [2,400]\ \text{km}$. The ratio between rotational and divergent energy is approximately three for
$r\in [2,400]\ \text{km}$. The ratio between rotational and divergent energy is approximately three for 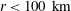 $r<100\ \text{km}$, excluding gravity waves also in this case. We argue that the possible errors in the decomposition at scales of the order of 10 km are marginal.
$r<100\ \text{km}$, excluding gravity waves also in this case. We argue that the possible errors in the decomposition at scales of the order of 10 km are marginal.