Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T08:56:42.971Z Has data issue: false hasContentIssue false
  • English
  • Français

Helicity in the Ekman boundary layer

Published online by Cambridge University Press:  26 August 2014

Enrico Deusebio  and
Erik Lindborg
Enrico Deusebio*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Cambridge CB3 0WA, UK Linné Flow Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
Erik Lindborg
Affiliation:
Linné Flow Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Helicity, which is defined as the scalar product of velocity and vorticity, 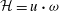$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathcal{H}} = {\boldsymbol {u}} \boldsymbol {\cdot }\boldsymbol{\omega}$, is an inviscidly conserved quantity in a barotropic fluid. Mean helicity is zero in flows that are parity invariant. System rotation breaks parity invariance and has therefore the potential of giving rise to non-zero mean helicity. In this paper we study the helicity dynamics in the incompressible Ekman boundary layer. Evolution equations for the mean field helicity and the mean turbulent helicity are derived and it is shown that pressure flux injects helicity at a rate 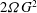$ 2 \varOmega G^2 $ over the total depth of the Ekman layer, where 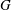$ G $ is the geostrophic wind far from the wall and 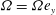$ {\boldsymbol{\Omega}} = \varOmega {\boldsymbol {e}}_y $ is the rotation vector and 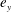$ {\boldsymbol {e}}_y $ is the wall-normal unit vector. Thus right-handed/left-handed helicity will be injected if 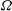$ \varOmega $ is positive/negative. We also show that in the uppermost part of the boundary layer there is a net helicity injection with opposite sign as compared with the totally integrated injection. Isotropic relations for the helicity dissipation and the helicity spectrum are derived and it is shown that it is sufficient to measure two transverse velocity components and use Taylor’s hypothesis in the mean flow direction in order to measure the isotropic helicity spectrum. We compare the theoretical predictions with a direct numerical simulation of an Ekman boundary layer and confirm that there is a preference for right-handed helicity in the lower part of the Ekman layer and left-handed helicity in the uppermost part when 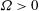$ \varOmega > 0 $. In the logarithmic range, the helicity dissipation conforms to isotropic relations. On the other hand, spectra show significant departures from isotropic conditions, suggesting that the Reynolds number considered in the study is not sufficiently large for isotropy to be valid in a wide range of scales. Our analytical and numerical results strongly suggest that there is a turbulent helicity cascade of right-handed helicity in the logarithmic range of the atmospheric boundary layer when 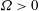$\varOmega >0$, consistent with recent measurements by Koprov, Koprov, Ponomarev & Chkhetiani (Dokl. Phys., vol. 50, 2005, pp. 419–422). The isotropic relations which are derived may facilitate future measurements of the helicity spectrum in the atmospheric boundary layer as well as in controlled wind tunnel experiments.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 755 , 25 September 2014 , pp. 654 - 671
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Biferale, L. 2003 Shell models of energy cascade in turbulence. Annu. Rev. Fluid Mech. 35 (1), 441–468.CrossRefGoogle Scholar
Biferale, L., Musacchio, S. & Toschi, F. 2012 Inverse energy cascade in three-dimensional isotropic turbulence. Phys. Rev. Lett. 108 (16), 164501.Google Scholar
Borue, V. & Orszag, S. A. 1997 Spectra in helical three-dimensional homogeneous isotropic turbulence. Phys. Rev. E 55 (6), 7005–7009.Google Scholar
Brissaud, A., Frisch, U., Leorat, J., Lesieur, M. & Mazure, A. 1973 Helicity cascades in fully developed isotropic turbulence. Phys. Fluids 16, 1366–1367.Google Scholar
Chen, Q., Chen, S. & Eyink, G. L. 2003a The joint cascade of energy and helicity in three-dimensional turbulence. Phys. Fluids 15, 361–374.Google Scholar
Chen, Q., Chen, S., Eyink, G. L. & Holm, D. D. 2003b Intermittency in the joint cascade of energy and helicity. Phys. Rev. Lett. 90 (21), 214503.Google Scholar
Chkhetiani, O. G. 1996 On the third moments in helical turbulence. J. Expl Theor. Phys. Lett. 63 (10), 808–812.Google Scholar
Deusebio, E.2013 Numerical studies in rotating and stratified turbulence. PhD thesis, KTH, Mechanics, Linné Flow Center, FLOW.Google Scholar
Deusebio, E., Brethouwer, G., Schlatter, P. & Lindborg, E. 2014 A numerical study of the unstratified and stratified Ekman layer. J. Fluid Mech. 755, 672–704.Google Scholar
Dhruva, B., Tsuji, Y. & Sreenivasan, K. R. 1997 Transverse structure functions in high-Reynolds-number turbulence. Phys. Rev. E 56, R4928–R4930.Google Scholar
El Khoury, G., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91, 475–495.Google Scholar
Etling, D. 1985 Some aspects of helicity in atmospheric flows. Beitr. Phys. Atmos. 58 (1), 88–100.Google Scholar
Gomez, T., Politano, H. & Pouquet, A. 2000 Exact relationship for third-order structure functions in helical flows. Phys. Rev. E 61 (5), 5321–5325.Google Scholar
Kholmyansky, M., Kit, E., Teitel, M. & Tsinober, A. 1991 Some experimental results on velocity and vorticity measurements in turbulent grid flows with controlled sign of mean helicity. Fluid Dyn. Res. 7 (2), 65–75.Google Scholar
Koprov, B. M., Koprov, V. M., Ponomarev, V. M. & Chkhetiani, O. G. 2005 Experimental studies of turbulent helicity and its spectrum in the atmospheric boundary layer. Dokl. Phys. 50, 419–422.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.Google Scholar
Kurien, S. 2003 The reflection-antisymmetric counterpart of the Kármán–Howarth dynamical equation. Physica D: Nonlinear Phenomena 175 (3), 167–176.Google Scholar
Lilly, D. K. 1986 The structure, energetics and propagation of rotating convective storms. Part II: helicity and storm stabilization. J. Atmos. Sci. 43 (2), 126–140.Google Scholar
Mininni, P. D., Alexakis, A. & Pouquet, A. 2006 Large-scale flow effects, energy transfer, and self-similarity on turbulence. Phys. Rev. E 74 (1), 016303.Google Scholar
Mininni, P. D. & Pouquet, A. 2009 Helicity cascades in rotating turbulence. Phys. Rev. E 79 (2), 026304.Google Scholar
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35 (1), 117–129.Google Scholar
Moffatt, H. K. 1981 Some developments in the theory of turbulence. J. Fluid Mech. 106, 27–47.Google Scholar
Moffatt, H. K. & Tsinober, A. 1992 Helicity in laminar and turbulent flow. Annu. Rev. Fluid Mech. 24 (1), 281–312.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Shingai, K. & Kawamura, H. 2004 A study of turbulence structure and large-scale motion in the Ekman layer through direct numerical simulations. J. Turbul. 5, N13.Google Scholar
Spalart, P. R., Coleman, G. N. & Johnstone, R. 2009 Retraction: direct numerical simulation of the Ekman layer: A step in Reynolds number, and cautious support for a log law with a shifted origin. Phys. Fluids 21 (10), 109901.Google Scholar
Thompson, R.2005 Explanation of SPC severe weather parameters. Available at http://www.spc.noaa.gov/sfctest/help/sfcoa.html.Google Scholar
Tsinober, A. & Levich, E. 1983 On the helical nature of three-dimensional coherent structures in turbulent flows. Phys. Lett. A 99 (6), 321–324.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation; Electronic Version. Cambridge University Press.Google Scholar
Zhemin, T. & Rongsheng, W. 1994 Helicity dynamics of atmospheric flow. Adv. Atmos. Sci. 11 (2), 175–188.CrossRefGoogle Scholar