Published online by Cambridge University Press: 03 December 2014
The thin helical vortex filament is one of the fundamental exact solutions possible under the local induction approximation (LIA). The LIA is itself an approximation to the non-local Biot–Savart dynamics governing the self-induced motion of a vortex filament, and helical filaments have also been considered for the Biot–Savart dynamics, under a variety of configurations and assumptions. We study the motion of such a helical filament in the Cartesian reference frame by determining the curve defining this filament mathematically from the Biot–Savart model. In order to do so, we consider a matched approximation to the Biot–Savart dynamics, with local effects approximated by the LIA in order to avoid the logarithmic singularity inherent in the Biot–Savart formulation. This, in turn, allows us to determine the rotational and translational velocity of the filament in terms of a local contribution (which is exactly that which is found under the LIA) and a non-local contribution, each of which depends on the wavenumber, 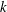 $k$, and the helix diameter,
$k$, and the helix diameter, 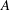 $A$. Performing our calculations in such a way, we can easily compare our results to those of the LIA. For small
$A$. Performing our calculations in such a way, we can easily compare our results to those of the LIA. For small 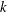 $k$, the transverse velocity scales as
$k$, the transverse velocity scales as 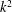 $k^{2}$, while for large
$k^{2}$, while for large 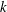 $k$, the transverse velocity scales as
$k$, the transverse velocity scales as 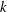 $k$. On the other hand, the rotational velocity attains a maximum value at some finite
$k$. On the other hand, the rotational velocity attains a maximum value at some finite 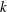 $k$, which corresponds to the wavenumber giving the maximal torsion.
$k$, which corresponds to the wavenumber giving the maximal torsion.