Published online by Cambridge University Press: 13 December 2016
We study the problem of mass transport to surfaces with heterogeneous reaction rates in the presence of shear flow over these surfaces. The reactions are first order and the heterogeneity is due to the existence of inert regions on the surfaces. Such problems are ubiquitous in the field of heterogeneous catalysis, electrochemistry and even biological mass transport. In these problems, the microscale reaction rate is characterized by a Damköhler number  $\unicode[STIX]{x1D705}$, while the Péclet number
$\unicode[STIX]{x1D705}$, while the Péclet number 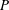 $P$ is the dimensionless ratio of the bulk shear rate to the inverse diffusion time scale. The area fraction of the reactive region is denoted by
$P$ is the dimensionless ratio of the bulk shear rate to the inverse diffusion time scale. The area fraction of the reactive region is denoted by 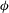 $\unicode[STIX]{x1D719}$. The objective is to calculate the yield of reaction, which is directly related to the mass flux to the reactive region, denoted by the dimensionless Sherwood number
$\unicode[STIX]{x1D719}$. The objective is to calculate the yield of reaction, which is directly related to the mass flux to the reactive region, denoted by the dimensionless Sherwood number 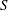 $S$. Previously, we used boundary element simulations and examined the case of first-order reactive disks embedded in an inert surface (Shah & Shaqfeh J. Fluid Mech., vol. 782, 2015, pp. 260–299). Various correlations for the Sherwood number as a function of
$S$. Previously, we used boundary element simulations and examined the case of first-order reactive disks embedded in an inert surface (Shah & Shaqfeh J. Fluid Mech., vol. 782, 2015, pp. 260–299). Various correlations for the Sherwood number as a function of 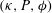 $(\unicode[STIX]{x1D705},P,\unicode[STIX]{x1D719})$ were obtained. In particular, we demonstrated that the ‘method of additive resistances’ provides a good approximation for the Sherwood number for a wide range of values of
$(\unicode[STIX]{x1D705},P,\unicode[STIX]{x1D719})$ were obtained. In particular, we demonstrated that the ‘method of additive resistances’ provides a good approximation for the Sherwood number for a wide range of values of 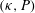 $(\unicode[STIX]{x1D705},P)$ for
$(\unicode[STIX]{x1D705},P)$ for 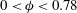 $0<\unicode[STIX]{x1D719}<0.78$. When
$0<\unicode[STIX]{x1D719}<0.78$. When 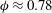 $\unicode[STIX]{x1D719}\approx 0.78$, the reactive disks are in a close packed configuration where the inert regions are essentially disconnected from each other. In this work, we develop an understanding of the physics when
$\unicode[STIX]{x1D719}\approx 0.78$, the reactive disks are in a close packed configuration where the inert regions are essentially disconnected from each other. In this work, we develop an understanding of the physics when 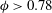 $\unicode[STIX]{x1D719}>0.78$, by examining the inverse problem of inert disks on a reactive surface. We show that the method of resistances approach to obtain the Sherwood number fails in the limit as
$\unicode[STIX]{x1D719}>0.78$, by examining the inverse problem of inert disks on a reactive surface. We show that the method of resistances approach to obtain the Sherwood number fails in the limit as 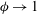 $\unicode[STIX]{x1D719}\rightarrow 1$, i.e. in the dilute limit of periodic inert disks, due to the existence of a surface concentration boundary layer around each disk that scales with (
$\unicode[STIX]{x1D719}\rightarrow 1$, i.e. in the dilute limit of periodic inert disks, due to the existence of a surface concentration boundary layer around each disk that scales with (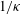 $1/\unicode[STIX]{x1D705}$). This boundary layer controls the screening length between inert disks and allows us to introduce a new theory, thus providing new correlations for the Sherwood number that are highly accurate in the limit of
$1/\unicode[STIX]{x1D705}$). This boundary layer controls the screening length between inert disks and allows us to introduce a new theory, thus providing new correlations for the Sherwood number that are highly accurate in the limit of 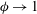 $\unicode[STIX]{x1D719}\rightarrow 1$.
$\unicode[STIX]{x1D719}\rightarrow 1$.