Published online by Cambridge University Press: 08 October 2015
Surfaces that include heterogeneous mass transfer at the microscale are ubiquitous in nature and engineering. Many such media are modelled via an effective surface reaction rate or mass transfer coefficient employing the conventional ansatz of kinetically limited transport at the microscale. However, this assumption is not always valid, particularly when there is strong flow. We are interested in modelling reactive and/or porous surfaces that occur in systems where the effective Damköhler number at the microscale can be 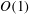 $O(1)$ and the local Péclet number may be large. In order to expand the range of the effective mass transfer surface coefficient, we study transport from a uniform bath of species in an unbounded shear flow over a flat surface. This surface has a heterogeneous distribution of first-order surface-reactive circular patches (or pores). To understand the physics at the length scale of the patch size, we first analyse the flux to a single reactive patch. We use both analytic and boundary element simulations for this purpose. The shear flow induces a 3-D concentration wake structure downstream of the patch. When two patches are aligned in the shear direction, the wakes interact to reduce the per patch flux compared with the single-patch case. Having determined the length scale of the interaction between two patches, we study the transport to a periodic and disordered distribution of patches again using analytic and boundary integral techniques. We obtain, up to non-dilute patch area fraction, an effective boundary condition for the transport to the patches that depends on the local mass transfer coefficient (or reaction rate) and shear rate. We demonstrate that this boundary condition replaces the details of the heterogeneous surfaces at a wall-normal effective slip distance also determined for non-dilute patch area fractions. The slip distance again depends on the shear rate, and weakly on the reaction rate, and scales with the patch size. These effective boundary conditions can be used directly in large-scale physics simulations as long as the local shear rate, reaction rate and patch area fraction are known.
$O(1)$ and the local Péclet number may be large. In order to expand the range of the effective mass transfer surface coefficient, we study transport from a uniform bath of species in an unbounded shear flow over a flat surface. This surface has a heterogeneous distribution of first-order surface-reactive circular patches (or pores). To understand the physics at the length scale of the patch size, we first analyse the flux to a single reactive patch. We use both analytic and boundary element simulations for this purpose. The shear flow induces a 3-D concentration wake structure downstream of the patch. When two patches are aligned in the shear direction, the wakes interact to reduce the per patch flux compared with the single-patch case. Having determined the length scale of the interaction between two patches, we study the transport to a periodic and disordered distribution of patches again using analytic and boundary integral techniques. We obtain, up to non-dilute patch area fraction, an effective boundary condition for the transport to the patches that depends on the local mass transfer coefficient (or reaction rate) and shear rate. We demonstrate that this boundary condition replaces the details of the heterogeneous surfaces at a wall-normal effective slip distance also determined for non-dilute patch area fractions. The slip distance again depends on the shear rate, and weakly on the reaction rate, and scales with the patch size. These effective boundary conditions can be used directly in large-scale physics simulations as long as the local shear rate, reaction rate and patch area fraction are known.