Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T07:50:42.113Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat transport properties of plates with smooth and rough surfaces in turbulent thermal convection

Published online by Cambridge University Press:  08 January 2014

Ping Wei ,
Tak-Shing Chan ,
Rui Ni ,
Xiao-Zheng Zhao  and
Ke-Qing Xia
Ping Wei
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Tak-Shing Chan
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Rui Ni
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Xiao-Zheng Zhao
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ke-Qing Xia*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

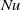We present an experimental study of turbulent thermal convection with smooth and rough surface plates in various combinations. A total of five cells were used in the experiments. Both the global $\mathit{Nu}$ and the 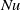$\mathit{Nu}$ for each plate (or the associated boundary layer) are measured. The results reveal that the smooth plates are insensitive to the surface (rough or smooth) and boundary conditions (i.e. nominally constant temperature or constant flux) of the other plate of the same cell. The heat transport properties of the rough plates, on the other hand, depend not only on the nature of the plate at the opposite side of the cell, but also on the boundary condition of that plate. It thus appears that, at the present level of experimental resolution, the smooth plate can influence the rough plate, but cannot be influenced by either the rough or the smooth plates. It is further found that the scaling of 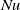$\mathit{Nu}$ with $\mathit{Ra}$ for all of the smooth plates is consistent with the classical 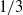$1/ 3$ exponent. But the scaling exponent for the global 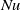$\mathit{Nu}$ for the cell with both plates being smooth is definitely less than 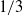$1/ 3$ (this result itself is consistent with all previous studies at comparable parameter range). The discrepancy between the 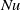$\mathit{Nu}$ behaviour at the whole-cell and individual-plate levels is not understood and deserves further investigation.

JFM classification

Boundary Layers: Boundary Layers Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 740 , 10 February 2014 , pp. 28 - 46
Copyright
©2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
van den Berg, T. H., Doering, C. R., Lohse, D. & Lathrop, D. P. 2003 Smooth and rough boundaries in turbulent Taylor–Couette flow. Phys. Rev. E 68, 036307.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 1–25.Google Scholar
Ciliberto, S. & Laroche, C. 1999 Random roughness of boundary increases the turbulent convection scaling exponent. Phys. Rev. Lett. 82, 3998–4001.Google Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.Google Scholar
Du, Y.-B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.CrossRefGoogle Scholar
Eckhardt, B., Grossann, S. & Lohse, D. 2000 Scaling of global momentum transport in Taylor–Couette and pipe flow. Eur. Phys. J. B 18, 541–544.CrossRefGoogle Scholar
Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
He, X.-Z., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultmate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.CrossRefGoogle Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102, 064501.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5 (11), 1374–1389.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Lui, S. L. & Xia, K.-Q. 1998 Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 57, 5494–5503.CrossRefGoogle Scholar
Malkus, M. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. Ser. A 225, 196–212.Google Scholar
Ni, R., Zhou, S.-Q. & Xia, K.-Q. 2011 An experimental investigation of turbulent thermal convection in water-based alumina nanofluid. Phys. Fluids 23, 022005.CrossRefGoogle Scholar
Qiu, X.-L., Xia, K.-Q. & Tong, P. 2005 Experimental study of velocity boundary layer near a rough conducting surface in turbulent natural convection. J. Turbul. 6 (30), 1–13.CrossRefGoogle Scholar
Roche, P. E., Castaing, B., Chabaud, B. & Hébral, B. 2001 Observation of the 1/2 power law in Rayleigh–Bénard convection. Phys. Rev. E 63, 045303.Google Scholar
Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q. 2003 Measured local heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 90, 074501.CrossRefGoogle ScholarPubMed
Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q. 2004 Measurements of the local convective heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. E 70, 026308.Google Scholar
Shang, X.-D., Tong, P. & Xia, K.-Q. 2008 Scaling of the local convective heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 100, 244503.CrossRefGoogle ScholarPubMed
Shen, Y., Tong, P. & Xia, K.-Q. 1996 Turbulent convection over rough surfaces. Phys. Rev. Lett. 76 (6), 908–911.Google Scholar
Stringano, G., Pascazio, G. & Verzicco, R. 2006 Turbulent thermal convection over grooved plates. J. Fluid Mech. 557, 307–336.Google Scholar
Sun, C., Xia, K.-Q. & Tong, P. 2005 Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72, 026302.Google Scholar
Tisserand, J.-C., Creyssels, M., Gasteuil, Y., Pabiou, H., Gibert, M., Castaing, B. & Chillà, F. 2011 Comparison between rough and smooth plates within the same Rayleigh–Bénard cell. Phys. Fluids 23 (1), 015105.Google Scholar
Wei, P., Ni, R. & Xia, K.-Q. 2012 Enhanced and reduced heat transport in turbulent thermal convection with polymer additives. Phys. Rev. E 86, 016325.CrossRefGoogle ScholarPubMed
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.Google Scholar
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 3, 052001.Google Scholar
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.CrossRefGoogle ScholarPubMed
Yaws, C. L. 1999 Chemical Properties Handbook: Physical, Thermodynamic, Environmental, Transport, Safety, and Health Related Properties for Organic and Inorganic Chemicals. McGraw-Hill.Google Scholar
Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2007 Measured oscillations of the velocity and temperature fields in turbulent Rayleigh–Bénard convection in a rectangular cell. Phys. Rev. E 76, 036301.Google Scholar