Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T08:41:41.525Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat transport and pressure buildup during carbon dioxide injection into depleted gas reservoirs

Published online by Cambridge University Press:  01 September 2014

Simon A. Mathias ,
Jim N. McElwaine  and
Jon G. Gluyas
Simon A. Mathias*
Affiliation:
Department of Earth Sciences, Durham University, Durham DH1 3LE, UK
Jim N. McElwaine
Affiliation:
Department of Earth Sciences, Durham University, Durham DH1 3LE, UK
Jon G. Gluyas
Affiliation:
Department of Earth Sciences, Durham University, Durham DH1 3LE, UK
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

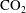In this article, a two-layer vertical equilibrium model for the injection of carbon dioxide into a low-pressure porous reservoir containing methane and water is developed. The dependent variables solved for include pressure, temperature and $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathrm{CO}}_2$–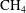${\mathrm{CH}}_4$ interface height. In contrast to previous two-layer vertical equilibrium models in this context, the compressibility of all material components is fully accounted for. Non-Darcy effects are also considered using the Forchheimer equation. The results show that, for a given injection scenario, as the initial pressure in the reservoir decreases, both the pressure buildup and temperature change increase. A comparison was conducted between a fully coupled non-isothermal numerical model and a simplified model where fluid properties are held constant with temperature. This simplified model was found to provide an excellent approximation when using the injection fluid temperature for calculating fluid properties, even when the injection fluid was as much as 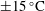$\pm 15\, ^\circ \mathrm{C}$ of the initial reservoir temperature. The implications are that isothermal models can be expected to provide useful estimates of pressure buildup in this context. Despite the low viscosity of 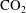${\mathrm{CO}}_2$ at the low pressures studied, non-Darcy effects were found to be of negligible concern throughout the sensitivity analysis undertaken. This is because the 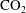${\mathrm{CO}}_2$ density is also low in this context. Based on these findings, simplified analytic solutions are derived, which accurately calculate both the pressure buildup and temperature decline during the injection period.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 89 - 109
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© 2014 Cambridge University Press

References

Afanasyev, A. A. 2013 Multiphase compositional modelling of ${\mathrm{CO}}_{2}$ injection under subcritical conditions: the impact of dissolution and phase transitions between liquid and gaseous ${\mathrm{CO}}_{2}$ on reservoir temperature. Intl J. Greenh. Gas Control 19, 731–742.CrossRefGoogle Scholar
Agarwal, R.1979 Real gas pseudo-time – a new function for pressure buildup analysis of MHF gas wells. In SPE Annual Technical Conference and Exhibition, SPE 8279-MS.Google Scholar
Al-Hussainy, R., Ramey, H. J. Jr. & Crawford, P. B. 1966 The flow of real gases through porous media. J. Petrol. Tech. 577, 363–383.Google Scholar
Andre, L., Azaroual, M. & Menjoz, A. 2010 Numerical simulations of the thermal impact of supercritical ${\mathrm{CO}}_2$ injection on chemical reactivity in a carbonate saline reservoir. Transp. Porous Med. 82, 247–274.Google Scholar
Bachu, S. & Bennion, B. 2008a Effects of in situ conditions on relative permeability characteristics of ${\mathrm{CO}}_{2}$ –brine systems. Environ. Geol. 54, 1707–1722.Google Scholar
Bachu, S. & Bennion, B. 2008b Interfacial tension between ${\mathrm{CO}}_{2}$ , freshwater, and brine in the range of pressure from (2 to 27) MPa, temperature from $(20\ \text {to}\ 125)\, ^\circ \mathrm{C}$ , and water salinity from $(0\ \text {to}\ 334\, 000)\ \mathrm{mg}\ {\mathrm{L}}^{-1}$ . J. Chem. Engng Data 54, 765–775.Google Scholar
Barrufet, M., Bacquet, A. & Falcone, G. 2010 Analysis of the storage capacity for ${\mathrm{CO}}_{2}$ sequestration of a depleted gas condensate reservoir and a saline aquifer. J. Can. Petrol. Technol. 49, 23–31.Google Scholar
Bentham, M. & Kirby, M. 2005 ${\mathrm{CO}}_{2}$ storage in saline aquifers. Oil Gas Sci. Technol. 60, 559–567.Google Scholar
Buckley, S. E. & Leverett, M. C. 1942 Mechanism of fluid displacement in sands. Trans. AIME 146, 107–116.Google Scholar
Cengel, Y. A. & Boles, M. A. 2002 Thermodynamics – An Engineering Approach, 4th edn. McGraw-Hill.Google Scholar
Chen, Z., Huan, G. & Ma, Y. 2006 Computational Methods for Multiphase Flows in Porous Media, Computational Science and Engineering Series, vol. 2. SIAM.Google Scholar
Geertsma, J. 1974 Estimating the coefficient of inertial resistance in fluid flow through porous media. Soc. Petrol. Engng J. 14, 445–450.Google Scholar
Gluyas, J. G. & Hichens, H. M. 2003 United Kingdom Oil and Gas Fields, Commemorative Millennium Volume, Geological Society Memoirs, no. 20. Geological Society.Google Scholar
Han, W. S., Kim, K. Y., Park, E., McPherson, B. J., Lee, S.-Y. & Park, M.-H. 2012 Modeling of spatiotemporal thermal response to ${\mathrm{CO}}_{2}$ injection in saline formations: interpretation for monitoring. Transp. Porous Med. 93, 381–399.Google Scholar
Han, W. S., Stillman, G. A., Lu, M., McPherson, B. J. & Park, E. 2010 Evaluation of potential non-isothermal processes and heat transport during ${\mathrm{CO}}_{2}$ sequestration. J. Geophys. Res. 115, B07209.Google Scholar
Hesse, M. A., Orr, F. M. & Tchelepi, H. A. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.Google Scholar
Hesse, M. A., Tchelepi, H. A., Cantwell, B. J. & Orr, F. M. Jr. 2007 Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid Mech. 577, 363–383.Google Scholar
Knobel, R. 1999 An Introduction to the Mathematical Theory of Waves. American Mathematical Society.CrossRefGoogle Scholar
Lemmon, E. E., McLinden, M. O. & Friend, D. G. 2013 Thermophysical properties of fluid systems. In NIST Chemistry WebBook, NIST Standard Reference Database, vol. 69. National Institute of Standards and Technology, (online).Google Scholar
Loizzo, M., Lecampion, B., Berard, T., Harichandran, A. & Jammes, L.2009 Reusing O&G depleted reservoirs for ${\mathrm{CO}}_2$ storage: pros and cons. In Offshore Europe Oil & Gas Conference & Exhibition, SPE-124317.Google Scholar
MacMinn, C. W., Szulczewski, M. L. & Juanes, R. 2010 ${\mathrm{CO}}_{2}$ migration in saline aquifers. Part 1. Capillary trapping under slope and groundwater flow. J. Fluid Mech. 662, 329–351.Google Scholar
MacMinn, C. W., Szulczewski, M. L. & Juanes, R. 2011 ${\mathrm{CO}}_{2}$ migration in saline aquifers. Part 2. Capillary and solubility trapping. J. Fluid Mech. 688, 321–351.Google Scholar
MacRoberts, D. T.1962 Abandonment pressure of gas wells. In SPE Petroleum Economics and Valuation Symposium, SPE-260-MS.Google Scholar
Mathias, S. A., Butler, A. P. & Zhan, H. 2008 Approximate solutions for Forchheimer flow to a well. J. Hydraul. Engng 134, 1318–1325.Google Scholar
Mathias, S. A., Gluyas, J. G., González Martínez de Miguel, G. J., Bryant, S. L. & Wilson, D. 2013a On relative permeability data uncertainty and ${\mathrm{CO}}_{2}$ injectivity estimation for brine aquifers. Intl J. Greenh. Gas Control 12, 200–212.Google Scholar
Mathias, S. A., Gluyas, J. G., González Martínez de Miguel, G. J. & Hosseini, S. A. 2011a Role of partial miscibility on pressure buildup due to constant rate injection of ${\mathrm{CO}}_2$ into closed and open brine aquifers. Water Resour. Res. 47, W12525.Google Scholar
Mathias, S. A., Gluyas, J. G., González Martínez de Miguel, G. J., Thatcher, K. E. & Zimmerman, R. W. 2011b Pressure buildup during ${\mathrm{CO}}_{2}$ injection into a closed brine aquifer. Transp. Porous Med. 89, 383–397.Google Scholar
Mathias, S. A., Gluyas, J. G., Mackay, E. J. & Goldthorpe, W. H. 2013b A statistical analysis of well production rates from UK oil and gas fields – implications for carbon capture and storage. Intl J. Greenh. Gas Control 19, 510–518.Google Scholar
Mathias, S. A., Gluyas, J. G., Oldenburg, C. M. & Tsang, C. F. 2010 Analytical solution for Joule–Thomson cooling during ${\mathrm{CO}}_2$ geo-sequestration in depleted oil and gas reservoirs. Intl J. Greenh. Gas Control 4, 806–810.Google Scholar
Mathias, S. A., Hardisty, P. E., Trudell, M. R. & Zimmerman, R. W. 2009 Approximate solutions for pressure buildup during ${\mathrm{CO}}_2$ injection in brine aquifers. Transp. Porous Med. 79, 265–284.Google Scholar
Mathias, S. A. & Todman, L. C. 2010 Step-drawdown tests and the Forchheimer equation. Water Resour. Res. 46, W07514.Google Scholar
Mijic, A., Mathias, S. A. & LaForce, T. C. 2013 Multiple well systems with non-Darcy flow. Ground Water 51, 588–596.Google Scholar
Mukhopadhyay, S., Yang, S. Y. & Yeh, H. D. 2012 Pressure buildup during supercritical carbon dioxide injection from a partially penetrating borehole into gas reservoirs. Transp. Porous Med. 91, 889–911.Google Scholar
Nield, D. A. & Bejan, A. 2006 Convection in Porous Media, 3rd edn. Springer.Google Scholar
Nordbotten, J. M. & Celia, M. A. 2006 Similarity solutions for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327.CrossRefGoogle Scholar
Okwananke, A., Yekeen Adeboye, B. & Sulaimon, L. A. 2011 Evaluation and performance of natural gas storage in depleted gas reservoirs. Petrol. Coal 53, 324–332.Google Scholar
Oldenberg, C. M. 2007 Joule–Thomson cooling due to ${\mathrm{CO}}_{2}$ injection into natural gas reservoirs. Energy Convers. Manage. 48, 1808–1815.Google Scholar
Ren, Q. Y., Chen, G. J., Yan, W. & Guo, T. M. 2000 Interfacial tension of ( ${\mathrm{CO}}_{2} + {\mathrm{CH}}_{4}) + \text {water}$ from 298 K to 373 K and pressures up to 30 MPa. J. Chem. Engng Data 45, 610–612.Google Scholar
Singh, A. K., Baumann, J., Henninges, J., Goerke, U. J. & Kolditz, O. 2012 Numerical analysis of thermal effects during carbon dioxide injection with enhanced gas recovery: a theoretical case study for the Altmark gas field. Environ. Earth Sci. 67, 497–509.CrossRefGoogle Scholar
Singh, A. K., Goerke, U. J. & Kolditz, O. 2011 Numerical simulation of non-isothermal compositional gas flow: application to carbon dioxide injection into gas reservoirs. Energy 36, 3446–3458.Google Scholar
Somerton, W. H. 1992 Thermal Properties and Temperature-Related Behavior of Rock/Fluid Systems, Developments in Petroleum Science, vol. 37. Elsevier.Google Scholar
Somerton, W. H., Janah, A. H. & Ashqar, P. I.1981 Thermal expansion of fluid saturated rocks under stress. In SPWLA 22nd Annual Logging Symposium, Society of Petrophysicists and Well-Log Analysts. SPWLA-1981-D.Google Scholar
Spycher, N., Pruess, K. & Ennis-King, J. 2003 ${\mathrm{CO}}_2\text {--}{\mathrm{H}}_{2}\mathrm{O}$ mixtures in the geological sequestration of ${\mathrm{CO}}_2$ . I. Assessment and calculation of mutual solubilities from $12\ \text {to}\ 100\, ^\circ \mathrm{C}$ and up to 600 bar. Geochim. Cosmochim. Acta 67, 3015–3031.Google Scholar
Zeidouni, M., Nicot, J. P. & Hovorka, S. D. 2013 Monitoring above-zone temperature variations associated with ${\mathrm{CO}}_{2}$ and brine leakage from a storage aquifer. Environ. Earth Sci. (in press).Google Scholar
Zeng, Z. & Grigg, R. 2006 A criterion for non-Darcy flow in porous media. Transp. Porous Med. 63, 57–69.CrossRefGoogle Scholar
Ziabaksh-Ganji, Z. & Kooi, O. 2014 Sensitivity of Joule–Thomson cooling to impure ${\mathrm{CO}}_{2}$ injection in depleted gas reservoirs. Appl. Energy 113, 434–451.Google Scholar
Zimmerman, R. W. 1989 Thermal conductivity of fluid-saturated rocks. J. Petrol. Sci. Engng 3, 219–227.Google Scholar
Zimmerman, R. W. 2000 Coupling in poroelasticity and thermoelasticity. J. Rock Mech. Min. Sci. 37, 79–87.Google Scholar