1. Introduction
The simultaneous increase of heat transfer and reduction of drag in laminar and turbulent fluid flows has turned out to be a considerable challenge. Such technology could lower the power input required for driving the flow in heat exchangers, microprocessors and other thermal systems. A common technique to increase heat transfer in applications is to use rough or modified walls (figure 1a). While roughness, grooves, blades, ridges and corrugations increase the surface heat flux, they also increase the momentum transport, resulting in increased drag (Rohsenow et al. Reference Rohsenow, Hartnett and Cho1998). Enhancement of heat transfer in pipes, channels and ducts can also be achieved by miniaturisation since this increases the surface-to-volume ratio. Effectively, more liquid is then in contact with the surface for a given volume flow rate. However, reduced dimensions also lead to increased wall friction so that the required pressure drop (and pumping power) increases.

Figure 1. (a) Current practice to increase heat transfer through wall modification and (b) suggested method by using LIS. The working (external) fluid and the infusing liquid are shown in blue and green, respectively. The solid is depicted in brown.
Both heat transfer increase and drag reduction can be achieved with complex surfaces having multiple degrees of freedom to tune the surface-flow interaction. One example is a liquid-infused surface (LIS). The infusing liquid creates dynamic interfaces that induce a slipping effect on the external flow while affecting wall-normal velocity fluctuations (figure 1b). The careful design of texture topology, liquid viscosity, thermal conductivity and surface tension enables the precise tuning of transport processes.
In previous studies, superhydrophobic surfaces (SHS) have been used to reduce friction while maintaining the benefits of reduced system size (see the review by Gong et al. Reference Gong, Shen, Dai, Li and Gong2021). Similar effects could be accomplished with a LIS. An analytical model of heat transfer in pipes with SHS or LIS, taking the reduced friction into account, was recently developed by Hatte & Pitchumani (Reference Hatte and Pitchumani2021). Indeed, reducing the pipe radius increased the advantage of using SHS and LIS. Ciri & Leonardi (Reference Ciri and Leonardi2021) designed LIS and SHS that increased heat transfer and decreased drag in direct numerical simulations of a turbulent channel flow. Out of the many investigated surface configurations, this occurred only for SHS with longitudinal grooves, dynamic interfaces and a gas–liquid thermal conductivity ratio of one. The solid structures were also assumed to have a constant temperature. A thermal conductivity ratio of one and isothermal textures are hard to realise in practice, however.
If the thermal conductivity of the solid texture is similar to a contiguous liquid, the heat flux in neither phase is trivial. These solid–liquid combinations are not rare in applications. For example, water has a higher thermal conductivity than polymer polydimethylsiloxane. LIS made from such materials can be expected to have a very different heat flux compared with LIS with isothermal surface textures. For metal solids, liquid metals may be used as infusing liquids. There has recently been an increased interest in using liquid gallium alloys with low toxicity in stretchable electronics (Dickey Reference Dickey2017). The thermal conductivity of gallium is comparable to that of steel. An overview of some properties of representative solids and liquids is given in table 1.
Table 1. Overview of thermal conductivity, ![]() $\kappa$, viscosity,
$\kappa$, viscosity, ![]() $\mu$, density,
$\mu$, density, ![]() $\rho$, and isobaric specific heat capacity,
$\rho$, and isobaric specific heat capacity, ![]() $c_p$, for some fluids and solids. (R, Rohsenow et al. (Reference Rohsenow, Hartnett and Cho1998); M, Mark (Reference Mark2009); L, Liu, Sheng & He (Reference Liu, Sheng and He2019); C, Cardarelli (Reference Cardarelli2018); VB, Van Buren & Smits (Reference Van Buren and Smits2017); K1, Kashiwagi et al. (Reference Kashiwagi, Oishi, Tanaka, Kubota and Makita1982); K2, Khasanshin, Shchamialiou & Poddubskij (Reference Khasanshin, Shchamialiou and Poddubskij2003)).
$c_p$, for some fluids and solids. (R, Rohsenow et al. (Reference Rohsenow, Hartnett and Cho1998); M, Mark (Reference Mark2009); L, Liu, Sheng & He (Reference Liu, Sheng and He2019); C, Cardarelli (Reference Cardarelli2018); VB, Van Buren & Smits (Reference Van Buren and Smits2017); K1, Kashiwagi et al. (Reference Kashiwagi, Oishi, Tanaka, Kubota and Makita1982); K2, Khasanshin, Shchamialiou & Poddubskij (Reference Khasanshin, Shchamialiou and Poddubskij2003)).

Using liquid and solid properties similar to those of existing materials, we have investigated whether convection in the texture of LIS with transverse grooves can increase the surface heat flux, considering both laminar and turbulent flows. This mode of heat transfer has either been neglected or has not been evaluated closer in earlier works. The study was performed by numerically solving the equations for the velocity and temperature fields. We considered the heat transfer between two external boundaries of different temperature. The heat transport mechanisms of this set-up are shown in figure 2(a).

Figure 2. (a) Heat transport mechanisms contributing to the heat flux. (b) Schematic illustration of an interface unit cell for LIS. The colours of the fluids and the solid are the same as in figure 1.
The remainder of the article has the following structure. Governing equations and definitions of relevant quantities are presented in § 2. In § 3, it is shown that the contribution from the convection in the texture to the total heat flux is necessary to consider when the thermal conductivity of the solid structures is similar to the infusing liquid. Setting the solid and liquid thermal conductivities to the same value, the relation between the surface convection, liquid, flow and geometric properties is described in § 4. Results from turbulent flow simulations are presented in § 5. Conclusions are given in § 6.
2. Governing equations
We consider the momentum, continuity and energy equations for an incompressible system
where ![]() $\rho$ is the density,
$\rho$ is the density, ![]() $t$ is the time,
$t$ is the time, ![]() $\boldsymbol {u}$ is the fluid velocity,
$\boldsymbol {u}$ is the fluid velocity, ![]() $P$ is the pressure,
$P$ is the pressure, ![]() $\mu$ is the fluid viscosity,
$\mu$ is the fluid viscosity, ![]() $c_p$ is the specific heat capacity,
$c_p$ is the specific heat capacity, ![]() $T$ is the temperature and
$T$ is the temperature and ![]() $\kappa$ is the thermal conductivity. The streamwise coordinate is
$\kappa$ is the thermal conductivity. The streamwise coordinate is ![]() $x$, the wall-normal
$x$, the wall-normal ![]() $y$, with
$y$, with ![]() $y = 0$ at the surface, and the spanwise
$y = 0$ at the surface, and the spanwise ![]() $z$. Equations (2.1) and (2.2) are valid in the domains occupied by the external fluid and the infusing (internal) liquid. In the region occupied by the solid, only (2.3) is valid and
$z$. Equations (2.1) and (2.2) are valid in the domains occupied by the external fluid and the infusing (internal) liquid. In the region occupied by the solid, only (2.3) is valid and ![]() $\boldsymbol {u} = 0$.
$\boldsymbol {u} = 0$.
The differences between the fluid properties can be expressed through the viscosity ratio ![]() $\mu _i/\mu _\infty$, the density ratio
$\mu _i/\mu _\infty$, the density ratio ![]() $\rho _i/\rho _\infty$, the specific heat capacity ratio
$\rho _i/\rho _\infty$, the specific heat capacity ratio ![]() $c_{p,i}/c_{p,\infty }$ and the thermal conductivity ratio
$c_{p,i}/c_{p,\infty }$ and the thermal conductivity ratio ![]() $\kappa _i/\kappa _\infty$, where the subscripts
$\kappa _i/\kappa _\infty$, where the subscripts ![]() $i$ and
$i$ and ![]() $\infty$ refer to the infusing and external fluids, respectively. For example, Rosenberg et al. (Reference Rosenberg, Van Buren, Fu and Smits2016) and Van Buren & Smits (Reference Van Buren and Smits2017) used a heptane–water system (among others) with
$\infty$ refer to the infusing and external fluids, respectively. For example, Rosenberg et al. (Reference Rosenberg, Van Buren, Fu and Smits2016) and Van Buren & Smits (Reference Van Buren and Smits2017) used a heptane–water system (among others) with ![]() $\mu _i/\mu _\infty = 0.43$,
$\mu _i/\mu _\infty = 0.43$, ![]() $\kappa _i/\kappa _\infty = 0.21$ and
$\kappa _i/\kappa _\infty = 0.21$ and ![]() $c_{p,i}/c_{p,\infty } = 0.53$ (see also table 1). For simplicity and clarity, we have assumed that densities and specific heat capacities in fluids and solid, and thermal conductivities in the fluids, are equal, i.e.
$c_{p,i}/c_{p,\infty } = 0.53$ (see also table 1). For simplicity and clarity, we have assumed that densities and specific heat capacities in fluids and solid, and thermal conductivities in the fluids, are equal, i.e.
where a subscript ![]() $s$ denotes solid properties.
$s$ denotes solid properties.
The velocity satisfies the no-slip and impermeability conditions at solid boundaries. Across liquid–liquid interfaces, the velocity and the shear stress are continuous (disregarding surface tension gradients, see Sundin & Bagheri Reference Sundin and Bagheri2022). We have neglected interface deformation, which is equivalent to imposing an infinite surface tension. Consequently, the wall-normal velocity component ![]() $v$ is zero at interfaces. The temperature and the (instantaneous and local) heat flux are continuous at solid boundaries and interfaces. Also, the temperature is a passive scalar, i.e. the momentum equation is independent of the energy equation.
$v$ is zero at interfaces. The temperature and the (instantaneous and local) heat flux are continuous at solid boundaries and interfaces. Also, the temperature is a passive scalar, i.e. the momentum equation is independent of the energy equation.
The surface-averaged heat flux, ![]() $q$, can be decomposed into different contributions using the Fukagata, Iwamoto and Kasagi (FIK) identity of the energy equation (Fukagata, Iwamoto & Kasagi Reference Fukagata, Iwamoto and Kasagi2005). In this decomposition, we consider a channel of height
$q$, can be decomposed into different contributions using the Fukagata, Iwamoto and Kasagi (FIK) identity of the energy equation (Fukagata, Iwamoto & Kasagi Reference Fukagata, Iwamoto and Kasagi2005). In this decomposition, we consider a channel of height ![]() $h$ and grooves of depth
$h$ and grooves of depth ![]() $k$ with a solid slab of the same thickness beneath (figure 2b). The solid slab allows for temperature variations below the grooves in the simulations. The derivation is outlined in Appendix A. The second term of (2.3) gives rise to two convection terms, and the third term gives rise to three conduction terms. In total, the expression for
$k$ with a solid slab of the same thickness beneath (figure 2b). The solid slab allows for temperature variations below the grooves in the simulations. The derivation is outlined in Appendix A. The second term of (2.3) gives rise to two convection terms, and the third term gives rise to three conduction terms. In total, the expression for ![]() $q$ is
$q$ is
 \begin{align} q &={-} \frac{\kappa_\infty}{h + 2k}\int_{0}^{h}\left\langle {\frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y - \frac{\kappa_s}{h + 2k}\int_{{-}2k}^{0}\left\langle {\frac{\partial T}{\partial y}\chi_s} \right\rangle\,\mathrm{d} y \nonumber\\ &\quad - \frac{\kappa_i}{h + 2k}\int_{{-}2k}^{0}\left\langle {\frac{\partial T}{\partial y}(1 - \chi_s)} \right\rangle\,\mathrm{d} y + \frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}\left\langle {v'T'} \right\rangle\,\mathrm{d} y + \frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}\,\mathrm{d} y \nonumber\\ &= q_{{cond},\infty} + q_{{cond},s} + q_{{cond},i} + q_{{conv},r} + q_{{conv},d}, \end{align}
\begin{align} q &={-} \frac{\kappa_\infty}{h + 2k}\int_{0}^{h}\left\langle {\frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y - \frac{\kappa_s}{h + 2k}\int_{{-}2k}^{0}\left\langle {\frac{\partial T}{\partial y}\chi_s} \right\rangle\,\mathrm{d} y \nonumber\\ &\quad - \frac{\kappa_i}{h + 2k}\int_{{-}2k}^{0}\left\langle {\frac{\partial T}{\partial y}(1 - \chi_s)} \right\rangle\,\mathrm{d} y + \frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}\left\langle {v'T'} \right\rangle\,\mathrm{d} y + \frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}\,\mathrm{d} y \nonumber\\ &= q_{{cond},\infty} + q_{{cond},s} + q_{{cond},i} + q_{{conv},r} + q_{{conv},d}, \end{align}
where ![]() $\chi _s$ is an indicator function equal to
$\chi _s$ is an indicator function equal to ![]() $1$ in the solid and
$1$ in the solid and ![]() $0$ elsewhere. The operator
$0$ elsewhere. The operator ![]() $\left \langle {} \right \rangle$ denotes the average in time and the streamwise and spanwise directions. We have separated the convective flux
$\left \langle {} \right \rangle$ denotes the average in time and the streamwise and spanwise directions. We have separated the convective flux ![]() $\left \langle {vT} \right \rangle$ into a dispersive and a random component,
$\left \langle {vT} \right \rangle$ into a dispersive and a random component, ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$ and
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$ and ![]() $\left \langle {v'T'} \right \rangle$, respectively (Appendix B). Dispersive fluctuations (
$\left \langle {v'T'} \right \rangle$, respectively (Appendix B). Dispersive fluctuations (![]() $\tilde { {v} }$ and
$\tilde { {v} }$ and ![]() $\tilde { {T} }$) are time-averaged deviations from the mean due to the spatially varying surface properties, and random fluctuations (
$\tilde { {T} }$) are time-averaged deviations from the mean due to the spatially varying surface properties, and random fluctuations (![]() $v'$ and
$v'$ and ![]() $T'$) are the remaining (turbulent) fluctuations.
$T'$) are the remaining (turbulent) fluctuations.
The first three terms on the last line of (2.5) describe conduction in the external liquid, the solid and the infusing liquid, respectively. The following two terms correspond to convection from random fluctuations and dispersive fluctuations in the vicinity of the surface, respectively. Each of these terms has its counterpart before the equality sign in the same order. They also correspond to the heat transport mechanisms represented in figure 2(a). It is mainly the recirculation in the grooves that gives rise to ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$, which results in
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$, which results in ![]() $q_{{conv},d}$. At every wall-normal location,
$q_{{conv},d}$. At every wall-normal location, ![]() $q$ needs to be the same since there is no heat source inside the fluids or the solid.
$q$ needs to be the same since there is no heat source inside the fluids or the solid.
The steady laminar flow problem was solved in an interface unit cell, illustrated in figure 2(b). These simulations were performed using the finite element solver FreeFem++ (Hecht Reference Hecht2012; Lācis et al. Reference Lācis, Sudhakar, Pasche and Bagheri2020). The height of the channel was ![]() $h = 2k$ so that the total domain height was
$h = 2k$ so that the total domain height was ![]() $4k$. At the upper boundary, we imposed a constant shear stress
$4k$. At the upper boundary, we imposed a constant shear stress ![]() $\tau _\infty$ and no normal stress. In the streamwise direction, periodic boundary conditions were imposed. We applied constant temperatures
$\tau _\infty$ and no normal stress. In the streamwise direction, periodic boundary conditions were imposed. We applied constant temperatures ![]() $T_u$ and
$T_u$ and ![]() $T_l$ at the upper and the lower boundaries, respectively. More details about the simulation set-up can be found in Appendix C. Details about the turbulent simulations are given in § 5. A Reynolds number and a Péclet number based on the external flow quantities were defined as
$T_l$ at the upper and the lower boundaries, respectively. More details about the simulation set-up can be found in Appendix C. Details about the turbulent simulations are given in § 5. A Reynolds number and a Péclet number based on the external flow quantities were defined as ![]() ${{Re}}_\infty = \rho U_\infty h/\mu _\infty$ and
${{Re}}_\infty = \rho U_\infty h/\mu _\infty$ and ![]() ${{Pe}}_\infty = \rho c_p U_\infty h/\kappa _\infty$, respectively, where
${{Pe}}_\infty = \rho c_p U_\infty h/\kappa _\infty$, respectively, where ![]() $U_\infty$ is the resulting (mean) streamwise velocity at the top boundary. The corresponding Prandtl number is
$U_\infty$ is the resulting (mean) streamwise velocity at the top boundary. The corresponding Prandtl number is ![]() ${{Pr}}_\infty = {{Pe}}_\infty /{{Re}}_\infty =c_p\mu _\infty /\kappa _\infty$.
${{Pr}}_\infty = {{Pe}}_\infty /{{Re}}_\infty =c_p\mu _\infty /\kappa _\infty$.
3. Heat flux for varying solid conductivity
In laminar flow, there are no random fluctuations that transport heat. It follows that in the decomposition of the heat flux, ![]() $q_{{conv},r} = 0$. Equation (2.5) reduces to
$q_{{conv},r} = 0$. Equation (2.5) reduces to
We will use the smooth-wall heat flux as a reference for the LIS simulations. If the surface of the laminar flow is smooth, two additional simplifications can be made. Since there is no spatially varying texture, the dispersive convection is zero. Neither is there infusing liquid conducting heat. The heat flux only depends on the conduction in the solid and the external fluid and can be evaluated to (Appendix A.1)
Notice that ![]() $q^{0}$ also depends on
$q^{0}$ also depends on ![]() $\kappa _s$, meaning that the reference heat flux changes with
$\kappa _s$, meaning that the reference heat flux changes with ![]() $\kappa _s$.
$\kappa _s$.
In figure 3(a), ![]() $q/q^{0}$ is shown for varying solid conductivity ratios,
$q/q^{0}$ is shown for varying solid conductivity ratios, ![]() $\kappa _s/\kappa _i$. The applied shear stress corresponds to
$\kappa _s/\kappa _i$. The applied shear stress corresponds to ![]() ${{Re}}_\infty = 100$ (neglecting the slight increase in
${{Re}}_\infty = 100$ (neglecting the slight increase in ![]() $U_\infty$ due to the finite slip velocity). We consider three values of the Prandtl number,
$U_\infty$ due to the finite slip velocity). We consider three values of the Prandtl number, ![]() ${{Pr}}_\infty = 1$,
${{Pr}}_\infty = 1$, ![]() $10$ and
$10$ and ![]() $100$, and three viscosity ratios,
$100$, and three viscosity ratios, ![]() $\mu _i/\mu _\infty = 0.1$,
$\mu _i/\mu _\infty = 0.1$, ![]() $1$ and
$1$ and ![]() $10$. For comparison, if the external fluid is water,
$10$. For comparison, if the external fluid is water, ![]() ${{Pr}}_\infty = 7$, and the range of viscosity ratios covers all liquids of table 1. The pitch (groove centre-to-centre distance) was
${{Pr}}_\infty = 7$, and the range of viscosity ratios covers all liquids of table 1. The pitch (groove centre-to-centre distance) was ![]() $p = 2k$, and the groove width
$p = 2k$, and the groove width ![]() $w = k$.
$w = k$.

Figure 3. (a) The change in ![]() $q/q^{0}$ because of varying
$q/q^{0}$ because of varying ![]() $\kappa _s$ for three different viscosity ratios and
$\kappa _s$ for three different viscosity ratios and ![]() ${{Pr}}_\infty = 1$,
${{Pr}}_\infty = 1$, ![]() $10$ and
$10$ and ![]() $100$ at
$100$ at ![]() ${{Re}}_\infty = 100$. Each marker represents a simulation result, and the lines connect markers corresponding to the same
${{Re}}_\infty = 100$. Each marker represents a simulation result, and the lines connect markers corresponding to the same ![]() $\mu _i/\mu _\infty$ and
$\mu _i/\mu _\infty$ and ![]() ${{Pr}}_\infty$. The ratio
${{Pr}}_\infty$. The ratio ![]() $q/q^{0}$ increases with increasing
$q/q^{0}$ increases with increasing ![]() ${{Pr}}_\infty$ for a fixed
${{Pr}}_\infty$ for a fixed ![]() $\kappa _s/\kappa _i$ and
$\kappa _s/\kappa _i$ and ![]() $\mu _i/\mu _\infty$, indicated by the arrow. The curves for
$\mu _i/\mu _\infty$, indicated by the arrow. The curves for ![]() ${{Pr}}_\infty = 1$ are almost on top of each other. The dashed line shows
${{Pr}}_\infty = 1$ are almost on top of each other. The dashed line shows ![]() $q/q^{0} = 1$. (b) The different contributions to
$q/q^{0} = 1$. (b) The different contributions to ![]() $q$ for
$q$ for ![]() $\kappa _s/\kappa _i = 0.5$,
$\kappa _s/\kappa _i = 0.5$, ![]() $1$, and
$1$, and ![]() $2$ at
$2$ at ![]() ${{Re}}_\infty = 100$,
${{Re}}_\infty = 100$, ![]() $\mu _i/\mu _\infty = 1$ and
$\mu _i/\mu _\infty = 1$ and ![]() ${{Pr}}_\infty = 10$.
${{Pr}}_\infty = 10$.
When ![]() $\kappa _s/\kappa _i = 1$, there is an increase in
$\kappa _s/\kappa _i = 1$, there is an increase in ![]() $q/q^{0}$ from unity because of convection. For smaller
$q/q^{0}$ from unity because of convection. For smaller ![]() $\kappa _s/\kappa _i$ – when the solid is a poor heat conductor compared with the infusing liquid – the average thermal conductivity of the composite surface is higher than for the solid alone, resulting in an even more pronounced increase in
$\kappa _s/\kappa _i$ – when the solid is a poor heat conductor compared with the infusing liquid – the average thermal conductivity of the composite surface is higher than for the solid alone, resulting in an even more pronounced increase in ![]() $q/q^{0}$. However, when
$q/q^{0}$. However, when ![]() $\kappa _s/\kappa _i$ is increased above unity, there is eventually a decrease in the surface heat flux. At approximately
$\kappa _s/\kappa _i$ is increased above unity, there is eventually a decrease in the surface heat flux. At approximately ![]() $\kappa _s/\kappa _i = 3$, the simulations result in
$\kappa _s/\kappa _i = 3$, the simulations result in ![]() $q/q^{0} < 1$, except for the highest
$q/q^{0} < 1$, except for the highest ![]() ${{Pr}}_\infty$ and the smallest viscosity ratio. It is thus necessary that
${{Pr}}_\infty$ and the smallest viscosity ratio. It is thus necessary that ![]() $\kappa _s \lesssim \kappa _i$ to have an increase in the heat flux.
$\kappa _s \lesssim \kappa _i$ to have an increase in the heat flux.
The different terms of (3.1) are illustrated in figure 3(b) for ![]() ${{Pr}}_\infty = 10$,
${{Pr}}_\infty = 10$, ![]() $\mu _i/\mu _\infty = 1$, and
$\mu _i/\mu _\infty = 1$, and ![]() $\kappa _s/\kappa _i = 0.5$,
$\kappa _s/\kappa _i = 0.5$, ![]() $1$ and
$1$ and ![]() $2$. In the case of the poor solid conductor (
$2$. In the case of the poor solid conductor (![]() $\kappa _s/\kappa _i = 0.5$),
$\kappa _s/\kappa _i = 0.5$), ![]() $q/q^{0}$ would be greater than unity even without convection, because of the heat conduction in the infusing liquid (
$q/q^{0}$ would be greater than unity even without convection, because of the heat conduction in the infusing liquid (![]() $q_{{cond},i}$). For a good solid conductor (
$q_{{cond},i}$). For a good solid conductor (![]() $\kappa _s/\kappa _i = 2$), the convection (
$\kappa _s/\kappa _i = 2$), the convection (![]() $q_{{cond},d}$) cannot compensate for the cutout of the solid that is the groove. However, for
$q_{{cond},d}$) cannot compensate for the cutout of the solid that is the groove. However, for ![]() $\kappa _s/\kappa _i = 1$, it is the convection that increases
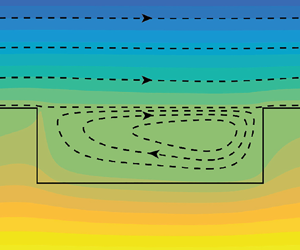
$\kappa _s/\kappa _i = 1$, it is the convection that increases ![]() $q/q^{0}$ above unity. Contour plots of the temperature fields of these three cases are shown in figure 4, together with streamlines. The streamlines indicate similarity between LIS and
$q/q^{0}$ above unity. Contour plots of the temperature fields of these three cases are shown in figure 4, together with streamlines. The streamlines indicate similarity between LIS and ![]() $d$-type roughness, with the external flow prevented from penetrating the texture (Jiménez Reference Jiménez2004); this behaviour is enforced by the interface and therefore also holds for larger values of
$d$-type roughness, with the external flow prevented from penetrating the texture (Jiménez Reference Jiménez2004); this behaviour is enforced by the interface and therefore also holds for larger values of ![]() $w/k$. The contour levels of the temperature field have less spacing in the region of higher conductivity. They are also distorted in and around the grooves due to convection. The convection increases the temperature on the left side of the cavity and decreases it on the right side.
$w/k$. The contour levels of the temperature field have less spacing in the region of higher conductivity. They are also distorted in and around the grooves due to convection. The convection increases the temperature on the left side of the cavity and decreases it on the right side.

Figure 4. Filled contour plots of the temperature at ![]() ${{Re}}_\infty = 100$,
${{Re}}_\infty = 100$, ![]() $\mu _i/\mu _\infty = 1$ and
$\mu _i/\mu _\infty = 1$ and ![]() ${{Pr}}_\infty = 10$, for (a)
${{Pr}}_\infty = 10$, for (a) ![]() $\kappa _s/\kappa _i = 0.5$, (b)
$\kappa _s/\kappa _i = 0.5$, (b) ![]() $\kappa _s/\kappa _i = 1$ and (c)
$\kappa _s/\kappa _i = 1$ and (c) ![]() $\kappa _s/\kappa _i = 2$. The colour bar gives the corresponding temperatures, ranging from
$\kappa _s/\kappa _i = 2$. The colour bar gives the corresponding temperatures, ranging from ![]() $T_u$ (
$T_u$ (![]() $0$) to
$0$) to ![]() $T_l$ (
$T_l$ (![]() $1$). Streamlines (white dashed lines) indicate the velocity field, computed as contour lines of the streamfunction (constant increment in the groove; showing a few in the external flow). The edges of the solid are marked with solid lines. In and around the groove, there is a distortion of the temperature field due to convection. The convection increases heat transfer in all three cases. However, in (a), the higher thermal conductivity in the infusing liquid also increases
$1$). Streamlines (white dashed lines) indicate the velocity field, computed as contour lines of the streamfunction (constant increment in the groove; showing a few in the external flow). The edges of the solid are marked with solid lines. In and around the groove, there is a distortion of the temperature field due to convection. The convection increases heat transfer in all three cases. However, in (a), the higher thermal conductivity in the infusing liquid also increases ![]() $q/q^{0}$. In (c), the solid has a higher thermal conductivity, reducing the benefit of the groove. The heat fluxes in and out of the groove are illustrated with arrows in (b). The attached numbers are the heat fluxes normalised by
$q/q^{0}$. In (c), the solid has a higher thermal conductivity, reducing the benefit of the groove. The heat fluxes in and out of the groove are illustrated with arrows in (b). The attached numbers are the heat fluxes normalised by ![]() $q$.
$q$.
We computed the heat fluxes through the different groove walls and the interface for the simulation in figure 4(b). These fluxes are also illustrated with arrows in the figure. Heat is transferred into (out of) the groove through the bottom wall (interface) and the right (left) wall. Through the interface, the heat flux was ![]() $q_I/q = 1.071$, i.e. slightly more than the average heat flux of the surface. The heat fluxes through the left, right and bottom walls were
$q_I/q = 1.071$, i.e. slightly more than the average heat flux of the surface. The heat fluxes through the left, right and bottom walls were ![]() $q_L/q = 0.160$,
$q_L/q = 0.160$, ![]() $q_R/q = 0.209$ and
$q_R/q = 0.209$ and ![]() $q_B/q = 1.021$, respectively (imbalance
$q_B/q = 1.021$, respectively (imbalance ![]() $|q_{err}|/q = 1.6\times 10^{-3}$). The increase of heat flux through the bottom wall,
$|q_{err}|/q = 1.6\times 10^{-3}$). The increase of heat flux through the bottom wall, ![]() $q_B > q$, and sides,
$q_B > q$, and sides, ![]() $q_R, q_L > 0$ is due to the convection of the cavity vortex. This convection is quantified by
$q_R, q_L > 0$ is due to the convection of the cavity vortex. This convection is quantified by ![]() $q_{{conv},d}$ and provides a net positive contribution to the total heat transfer of the surface (figure 3b).
$q_{{conv},d}$ and provides a net positive contribution to the total heat transfer of the surface (figure 3b).
4. Properties of the dispersive convection
In the previous section, it was illustrated how the heat flux depends on ![]() $\kappa _s/\kappa _i$. We now focus on the dependency on the fluid and flow properties expressed through
$\kappa _s/\kappa _i$. We now focus on the dependency on the fluid and flow properties expressed through ![]() ${{Pr}}_\infty$ and
${{Pr}}_\infty$ and ![]() ${{Re}}_\infty$. Since
${{Re}}_\infty$. Since ![]() $q_{{conv},d}$ is responsible for
$q_{{conv},d}$ is responsible for ![]() $q/q^{0}$ increasing above unity when the thermal conductivities are similar, the discussion is limited to
$q/q^{0}$ increasing above unity when the thermal conductivities are similar, the discussion is limited to ![]() $\kappa _s/\kappa _i = 1$. The heat then diffuses at the same rate in the solid as in the liquid, and the sum of the conduction terms can be simplified (Appendix A.2), leading to
$\kappa _s/\kappa _i = 1$. The heat then diffuses at the same rate in the solid as in the liquid, and the sum of the conduction terms can be simplified (Appendix A.2), leading to
 \begin{align} q = q_{{cond},\infty} + q_{{cond},s} + q_{{cond},i} + q_{{conv},d} = \underbrace{\frac{\kappa_\infty}{h + 2k}(T_l - T_u)}_{q_{{cond},\infty} + q_{{cond},s} + q_{{cond},i}} + \underbrace{\frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}\,\mathrm{d} y}_{q_{{conv},d}}. \end{align}
\begin{align} q = q_{{cond},\infty} + q_{{cond},s} + q_{{cond},i} + q_{{conv},d} = \underbrace{\frac{\kappa_\infty}{h + 2k}(T_l - T_u)}_{q_{{cond},\infty} + q_{{cond},s} + q_{{cond},i}} + \underbrace{\frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}\,\mathrm{d} y}_{q_{{conv},d}}. \end{align}
The sum of the conduction terms is denoted by ![]() $q_{cond}$ and corresponds to
$q_{cond}$ and corresponds to ![]() $q^{0}$ (3.2).
$q^{0}$ (3.2).
The relative contribution from convection to the total heat flux, ![]() $q_{{conv},d}/q$, is shown in figure 5(a) as a function of
$q_{{conv},d}/q$, is shown in figure 5(a) as a function of ![]() ${{Re}}_\infty$. These results were obtained for
${{Re}}_\infty$. These results were obtained for ![]() $\mu _i/\mu _\infty = 1$ and
$\mu _i/\mu _\infty = 1$ and ![]() ${{Pr}}_\infty = 0.1$,
${{Pr}}_\infty = 0.1$, ![]() $1$,
$1$, ![]() $10$ and
$10$ and ![]() $100$, each curve corresponding to a specific Prandtl number. For a constant
$100$, each curve corresponding to a specific Prandtl number. For a constant ![]() ${{Re}}_\infty$,
${{Re}}_\infty$, ![]() $q_{{conv},d}/q$ increases with
$q_{{conv},d}/q$ increases with ![]() ${{Pr}}_\infty$, as is indicated in figure 3(a). If
${{Pr}}_\infty$, as is indicated in figure 3(a). If ![]() $q_{{conv},d}/q$ instead is expressed as a function of
$q_{{conv},d}/q$ instead is expressed as a function of ![]() ${{Pe}}_\infty = {{Re}}_\infty {{Pr}}_\infty$, the curves collapse, as shown in figure 5(b). In this figure, we also include the results for
${{Pe}}_\infty = {{Re}}_\infty {{Pr}}_\infty$, the curves collapse, as shown in figure 5(b). In this figure, we also include the results for ![]() $\mu _i/\mu _\infty = 0.1$ and
$\mu _i/\mu _\infty = 0.1$ and ![]() $\mu _i/\mu _\infty = 10$, however. For a specific
$\mu _i/\mu _\infty = 10$, however. For a specific ![]() ${{Pe}}_\infty$, there is a dependency of
${{Pe}}_\infty$, there is a dependency of ![]() $q_{{conv},d}/q$ on the viscosity ratio. Even if
$q_{{conv},d}/q$ on the viscosity ratio. Even if ![]() ${{Re}}_\infty$ is constant, the magnitude of the flow inside the groove changes with viscosity ratio, and thereby the dispersive convection. Therefore, we need to define Reynolds and Péclet numbers that better characterise the flow at the surface.
${{Re}}_\infty$ is constant, the magnitude of the flow inside the groove changes with viscosity ratio, and thereby the dispersive convection. Therefore, we need to define Reynolds and Péclet numbers that better characterise the flow at the surface.

Figure 5. The relative contribution to the heat flux from convection as a function of (a) ![]() ${{Re}}_\infty$, (b)
${{Re}}_\infty$, (b) ![]() ${{Pe}}_\infty$ and (c)
${{Pe}}_\infty$ and (c) ![]() ${{Pe}}_i$. In (a), results for
${{Pe}}_i$. In (a), results for ![]() $\mu _i/\mu _\infty = 1$ are shown; (b,c) contain results for
$\mu _i/\mu _\infty = 1$ are shown; (b,c) contain results for ![]() $\mu _i/\mu _\infty = 0.1$,
$\mu _i/\mu _\infty = 0.1$, ![]() $1$ and
$1$ and ![]() $10$ (colours and symbols as in figure 3a). Prandtl numbers are
$10$ (colours and symbols as in figure 3a). Prandtl numbers are ![]() ${{Pr}}_\infty = 0.1$,
${{Pr}}_\infty = 0.1$, ![]() $1$,
$1$, ![]() $10$ and
$10$ and ![]() $100$. The ratio
$100$. The ratio ![]() $q_{{conv},d}/q$ increases with
$q_{{conv},d}/q$ increases with ![]() ${{Pr}}_\infty$ for a specific
${{Pr}}_\infty$ for a specific ![]() ${{Re}}_\infty$ (lines connect markers of identical
${{Re}}_\infty$ (lines connect markers of identical ![]() $\mu _i/\mu _\infty$ and
$\mu _i/\mu _\infty$ and ![]() ${{Pr}}_\infty$). For a certain viscosity ratio, the curves collapse if expressed as a function of
${{Pr}}_\infty$). For a certain viscosity ratio, the curves collapse if expressed as a function of ![]() ${{Pe}}_\infty$. However, if defined as a function of
${{Pe}}_\infty$. However, if defined as a function of ![]() ${{Pe}}_i$, they all collapse. The black dash-dotted line in (c) is (4.3).
${{Pe}}_i$, they all collapse. The black dash-dotted line in (c) is (4.3).
4.1. Surface Reynolds and Péclet numbers
A representative velocity of the flow in the grooves is the mean velocity at the interface. If it is averaged over the whole surface, it equals the slip velocity ![]() $U_s$, which is
$U_s$, which is ![]() $\left \langle {u} \right \rangle$ at
$\left \langle {u} \right \rangle$ at ![]() $y = 0$, where
$y = 0$, where ![]() $u$ is the streamwise velocity component. Using
$u$ is the streamwise velocity component. Using ![]() $U_s$ and
$U_s$ and ![]() $k$ as velocity and length scales, respectively, we define Reynolds and Péclet numbers as
$k$ as velocity and length scales, respectively, we define Reynolds and Péclet numbers as
together with a Prandtl number ![]() ${{Pr}}_i = {{Pe}}_i/{{Re}}_i=c_p\mu _i/\kappa _i$. Curves for different viscosity ratios collapse if
${{Pr}}_i = {{Pe}}_i/{{Re}}_i=c_p\mu _i/\kappa _i$. Curves for different viscosity ratios collapse if ![]() $q_{{conv},d}/q$ is expressed as a function of
$q_{{conv},d}/q$ is expressed as a function of ![]() ${{Pe}}_i$, as shown in figure 5(c).
${{Pe}}_i$, as shown in figure 5(c).
For ![]() ${{Pe}}_i \gtrsim 1$, there is a noticeable increase in
${{Pe}}_i \gtrsim 1$, there is a noticeable increase in ![]() $q_{{conv},d}/q$. At
$q_{{conv},d}/q$. At ![]() ${{Pe}}_i = 10$,
${{Pe}}_i = 10$, ![]() $q_{{conv},d}/q$ is greater than 1 %. The simulation results in figure 5(c) are well approximated by a logarithmic function for
$q_{{conv},d}/q$ is greater than 1 %. The simulation results in figure 5(c) are well approximated by a logarithmic function for ![]() $10^{1} < {{Pe}}_i < 10^{3}$. This set of
$10^{1} < {{Pe}}_i < 10^{3}$. This set of ![]() ${{Pe}}_i$ is the vital interval in practice, as it results in significant increases in heat transfer while still being attainable. The logarithmic function shown in the figure is
${{Pe}}_i$ is the vital interval in practice, as it results in significant increases in heat transfer while still being attainable. The logarithmic function shown in the figure is
found by fitting the data. This relationship is different from the power laws used for the similar problem of a lid-driven cavity (Moallemi & Jang Reference Moallemi and Jang1992). Here, the logarithmic expression gives a better fit. For comparison, the root-mean-squared error of the logarithmic expression was 0.0054, whereas, for a power-law fit of ![]() $\alpha ({{Pe}}_i^{\beta } - 1)$, it was 0.011, where
$\alpha ({{Pe}}_i^{\beta } - 1)$, it was 0.011, where ![]() $\alpha = 0.73k/(h + 2k)$ and
$\alpha = 0.73k/(h + 2k)$ and ![]() $\beta = 0.11$ (with
$\beta = 0.11$ (with ![]() $-1$ added assuming
$-1$ added assuming ![]() $q_{{conv},d} = 0$ when
$q_{{conv},d} = 0$ when ![]() ${{Pe}}_i = 1$).
${{Pe}}_i = 1$).
The relationships between ![]() ${{Re}}_\infty$ and
${{Re}}_\infty$ and ![]() ${{Re}}_i$ obtained from the simulations are plotted in figure 6(a). The slip velocity is related to the wall-normal derivative of
${{Re}}_i$ obtained from the simulations are plotted in figure 6(a). The slip velocity is related to the wall-normal derivative of ![]() $U = \left \langle {u} \right \rangle$ as
$U = \left \langle {u} \right \rangle$ as ![]() $U_s = b \,\mathrm {d} U/\mathrm {d} y|_{y = 0}$, where
$U_s = b \,\mathrm {d} U/\mathrm {d} y|_{y = 0}$, where ![]() $b$ is the (effective) slip length, and
$b$ is the (effective) slip length, and ![]() $\mathrm {d} U/\mathrm {d} y$ is evaluated at the interface in the external fluid. Since
$\mathrm {d} U/\mathrm {d} y$ is evaluated at the interface in the external fluid. Since ![]() $U_\infty = (h + b)\,\mathrm {d} U/\mathrm {d} y|_{y = 0}$, the
$U_\infty = (h + b)\,\mathrm {d} U/\mathrm {d} y|_{y = 0}$, the ![]() ${{Re}}_\infty$-to-
${{Re}}_\infty$-to-![]() ${{Re}}_i$ relation is a function of
${{Re}}_i$ relation is a function of ![]() $b$ (Appendix D). Slip lengths have also been derived analytically in the Stokes limit (
$b$ (Appendix D). Slip lengths have also been derived analytically in the Stokes limit (![]() ${{Re}}_\infty \rightarrow 0$) by Schönecker, Baier & Hardt (Reference Schönecker, Baier and Hardt2014), with the corresponding
${{Re}}_\infty \rightarrow 0$) by Schönecker, Baier & Hardt (Reference Schönecker, Baier and Hardt2014), with the corresponding ![]() ${{Re}}_\infty$-to-
${{Re}}_\infty$-to-![]() ${{Re}}_i$ relations also shown in figure 6(a). There is reasonable agreement between the Stokes flow results and the simulations up to moderate
${{Re}}_i$ relations also shown in figure 6(a). There is reasonable agreement between the Stokes flow results and the simulations up to moderate ![]() ${{Re}}_i$ (
${{Re}}_i$ (![]() $16\,\%$ difference for
$16\,\%$ difference for ![]() ${{Re}}_i = 19$ with
${{Re}}_i = 19$ with ![]() $\mu _i/\mu _\infty = 0.1$), indicating that the flow field in the cavities remains similar. Analytical slip lengths normalised by the pitch are plotted in figure 6(b).
$\mu _i/\mu _\infty = 0.1$), indicating that the flow field in the cavities remains similar. Analytical slip lengths normalised by the pitch are plotted in figure 6(b).

Figure 6. (a) The Reynolds number of the flow in the grooves, ![]() ${{Re}}_i$, expressed as a function of the external flow Reynolds number,
${{Re}}_i$, expressed as a function of the external flow Reynolds number, ![]() ${{Re}}_\infty$, for
${{Re}}_\infty$, for ![]() $p/k = 2$ and three different viscosity ratios (
$p/k = 2$ and three different viscosity ratios (![]() $\mu _i/\mu _\infty = 0.1$,
$\mu _i/\mu _\infty = 0.1$, ![]() $1$ and
$1$ and ![]() $10$, with colours and symbols as in figure 3a). The relation is approximately linear for low Reynolds numbers. The linearity is made visible by the lines
$10$, with colours and symbols as in figure 3a). The relation is approximately linear for low Reynolds numbers. The linearity is made visible by the lines ![]() ${{Re}}_i = {{Re}}_\infty b/(h + b) \boldsymbol {\cdot } k\mu _\infty /(h\mu _i)$, with
${{Re}}_i = {{Re}}_\infty b/(h + b) \boldsymbol {\cdot } k\mu _\infty /(h\mu _i)$, with ![]() $b$ predicted for Stokes flow (black). (b) The derived Stokes limit slip lengths over the pitch,
$b$ predicted for Stokes flow (black). (b) The derived Stokes limit slip lengths over the pitch, ![]() $b/p$, for
$b/p$, for ![]() $p/k = 2$,
$p/k = 2$, ![]() $4$ and 8, and groove width
$4$ and 8, and groove width ![]() $w = p - k$.
$w = p - k$.
In figure 7, ![]() $q_{{conv},d}/q$ is shown for other cavity widths and pitches. For
$q_{{conv},d}/q$ is shown for other cavity widths and pitches. For ![]() $p/k = 4$ and the same vertical wall thickness, there is a reasonable agreement with (4.3) (figure 7a). This texture corresponds to a solid fraction
$p/k = 4$ and the same vertical wall thickness, there is a reasonable agreement with (4.3) (figure 7a). This texture corresponds to a solid fraction ![]() $\phi _s = 1/4$ (i.e.
$\phi _s = 1/4$ (i.e. ![]() $1 - w/p$). For
$1 - w/p$). For ![]() $p/k = 4$ and
$p/k = 4$ and ![]() $\phi _s = 1/2$, it also holds (figure 7b). However, for
$\phi _s = 1/2$, it also holds (figure 7b). However, for ![]() $\phi _s = 3/4$, the increase of
$\phi _s = 3/4$, the increase of ![]() $q_{{conv},d}/q$ with
$q_{{conv},d}/q$ with ![]() ${{Pe}}_i$ is slower (figure 7c). For
${{Pe}}_i$ is slower (figure 7c). For ![]() $p/k = 8$, the relation is valid for
$p/k = 8$, the relation is valid for ![]() $\phi _s = 1/8$ and
$\phi _s = 1/8$ and ![]() $\phi _s = 1/2$ but not for
$\phi _s = 1/2$ but not for ![]() $\phi _s = 3/4$ (figure 7d–f). Based on these simulations, it is clear that (4.3) holds at least in the interval
$\phi _s = 3/4$ (figure 7d–f). Based on these simulations, it is clear that (4.3) holds at least in the interval ![]() $2 \le p/k \le 8$ for
$2 \le p/k \le 8$ for ![]() $\phi _s \le 1/2$,
$\phi _s \le 1/2$, ![]() $10^{1} < {{Pe}}_i < 10^{3}$,
$10^{1} < {{Pe}}_i < 10^{3}$, ![]() $\kappa _s = \kappa _i = \kappa _\infty$ and not too thin vertical walls (
$\kappa _s = \kappa _i = \kappa _\infty$ and not too thin vertical walls (![]() $p-w\ge k$).
$p-w\ge k$).

Figure 7. The relative contribution to the heat flux from convection for (a–c) ![]() $p/k = 4$ and (d–f)
$p/k = 4$ and (d–f) ![]() $p/k = 8$. The colours and symbols represent viscosity ratios as in figure 3(a), and the same
$p/k = 8$. The colours and symbols represent viscosity ratios as in figure 3(a), and the same ![]() ${{Pr}}_\infty$ as in figure 5 were used. Equation (4.3) is also shown (dashed-dotted line). The solver did not converge for some of the higher
${{Pr}}_\infty$ as in figure 5 were used. Equation (4.3) is also shown (dashed-dotted line). The solver did not converge for some of the higher ![]() ${{Re}}_i$, so these points have been removed.
${{Re}}_i$, so these points have been removed.
Assuming that ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$ is approximately zero above the grooves (
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$ is approximately zero above the grooves (![]() $y\geq 0$) – this is confirmed in figure 10(a) and discussed more later – we obtain,
$y\geq 0$) – this is confirmed in figure 10(a) and discussed more later – we obtain,
 \begin{equation} \frac{q_{{conv},d}}{q} = \frac{1}{h + 2k}\int_{{-}k}^{h}\frac{\rho c_p{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}}{q}\,\mathrm{d} y \approx \frac{1}{h + 2k}\int_{{-}k}^{0}\frac{\rho c_p{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}}{q}\,\mathrm{d} y < \frac{k}{h + 2k}. \end{equation}
\begin{equation} \frac{q_{{conv},d}}{q} = \frac{1}{h + 2k}\int_{{-}k}^{h}\frac{\rho c_p{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}}{q}\,\mathrm{d} y \approx \frac{1}{h + 2k}\int_{{-}k}^{0}\frac{\rho c_p{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}}{q}\,\mathrm{d} y < \frac{k}{h + 2k}. \end{equation}
This inequality is based on the assumption ![]() $\rho c_p{{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }} < q$, i.e.
$\rho c_p{{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }} < q$, i.e. ![]() $\mathrm {d} \left \langle {T} \right \rangle /\mathrm {d} y < 0$, which has been seen to be violated locally for high
$\mathrm {d} \left \langle {T} \right \rangle /\mathrm {d} y < 0$, which has been seen to be violated locally for high ![]() ${{Pr}}_\infty$ but by a negligible amount (figure 13f). The ratio
${{Pr}}_\infty$ but by a negligible amount (figure 13f). The ratio ![]() $k/(h + 2k)$ is thus an approximate upper limit of
$k/(h + 2k)$ is thus an approximate upper limit of ![]() $q_{{conv},d}/q$, and (4.3) cannot be expected to be valid for
$q_{{conv},d}/q$, and (4.3) cannot be expected to be valid for ![]() ${{Pe}}_i \gg 10^{3}$. For the laminar simulations (
${{Pe}}_i \gg 10^{3}$. For the laminar simulations (![]() $h = 2k$), the limiting value is
$h = 2k$), the limiting value is ![]() $25\,\%$. Moreover, from (2.5), one may see that
$25\,\%$. Moreover, from (2.5), one may see that ![]() $q_{{conv},d}\propto k/(h + 2k)$. For the investigated groove widths (
$q_{{conv},d}\propto k/(h + 2k)$. For the investigated groove widths (![]() $1 \le w/k \le 7$), the vertical size of the vortices in the grooves is approximately
$1 \le w/k \le 7$), the vertical size of the vortices in the grooves is approximately ![]() $k$. Therefore, the integral of
$k$. Therefore, the integral of ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$ scales with
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$ scales with ![]() $k$. The definition of
$k$. The definition of ![]() $q_{{conv},d}$ then results in the scaling with
$q_{{conv},d}$ then results in the scaling with ![]() $k/(h + 2k)$ (2.5), which was used in (4.3).
$k/(h + 2k)$ (2.5), which was used in (4.3).
4.2. Surface Nusselt number
Since the dispersive convection mainly is contained in the grooves, it is possible to quantify the heat transfer through the LIS by a surface Nusselt number. We consider only the texture, equivalent to ![]() $h = 0$, and define average temperatures at the interface (the slip temperature) and the bottom of the texture,
$h = 0$, and define average temperatures at the interface (the slip temperature) and the bottom of the texture, ![]() $T_s = \left \langle {T} \right \rangle |_{y = 0}$ and
$T_s = \left \langle {T} \right \rangle |_{y = 0}$ and ![]() $T_{lt} = \left \langle {T} \right \rangle |_{y = -k}$, respectively. The surface Nusselt number becomes (Appendix E)
$T_{lt} = \left \langle {T} \right \rangle |_{y = -k}$, respectively. The surface Nusselt number becomes (Appendix E)
The inequality in (4.4), applied to the texture only, limits ![]() ${{Nu}}_i$ to finite positive values.
${{Nu}}_i$ to finite positive values.
Heat exchangers can be represented by thermal resistance circuits (Rohsenow et al. Reference Rohsenow, Hartnett and Cho1998). The thermal resistances of the circuit components, proportional to the inverse of their Nusselt numbers, are then evaluated separately. These resistances can then be added to form the total thermal resistance of the system if they are in series. Hatte & Pitchumani (Reference Hatte and Pitchumani2021) constructed such a model to describe convective heat transfer in pipes with LIS, with the texture and the bulk as components. However, they implicitly neglected the dispersive convection by imposing ![]() ${{Nu}}_i = 1$. Since
${{Nu}}_i = 1$. Since ![]() ${{Nu}}_i > 1$ with convection included (see 4.5), the resulting heat flux of the complete system is higher than their model predicts. In the upper limit of (4.4) applied to the texture,
${{Nu}}_i > 1$ with convection included (see 4.5), the resulting heat flux of the complete system is higher than their model predicts. In the upper limit of (4.4) applied to the texture, ![]() ${{Nu}}_i \rightarrow \infty$. Accordingly, the thermal resistance of the surface becomes zero. Equation (4.5), together with (4.3) to describe
${{Nu}}_i \rightarrow \infty$. Accordingly, the thermal resistance of the surface becomes zero. Equation (4.5), together with (4.3) to describe ![]() $q_{{conv},d}/q$, could be used for a more precise evaluation of
$q_{{conv},d}/q$, could be used for a more precise evaluation of ![]() ${{Nu}}_i$ for the parameters and surface geometry considered in this study.
${{Nu}}_i$ for the parameters and surface geometry considered in this study.
5. Flow with turbulence
We have carried out simulations of a turbulent channel flow with LIS using a finite difference method. The bulk Reynolds number was set to ![]() ${{Re}}_b = \rho U_b H/\mu _\infty = 2800$, resulting in a friction Reynolds number of
${{Re}}_b = \rho U_b H/\mu _\infty = 2800$, resulting in a friction Reynolds number of ![]() ${{Re}}_\tau = \rho u_\tau H/\mu _\infty \approx 180$, where
${{Re}}_\tau = \rho u_\tau H/\mu _\infty \approx 180$, where ![]() $H = h/2$ is the channel half-height,
$H = h/2$ is the channel half-height, ![]() $U_b$ is the bulk velocity and
$U_b$ is the bulk velocity and ![]() $u_\tau$ is the friction velocity. A constant mass flow rate was achieved by applying a uniform volume force in the infusing and external liquids. The simulation domain is illustrated in figure 8. It had dimensions
$u_\tau$ is the friction velocity. A constant mass flow rate was achieved by applying a uniform volume force in the infusing and external liquids. The simulation domain is illustrated in figure 8. It had dimensions ![]() $(L_x, L_y, L_z) = (6.4H, 2H + 2k, 3.2H)$, and the number of grid points was
$(L_x, L_y, L_z) = (6.4H, 2H + 2k, 3.2H)$, and the number of grid points was ![]() $(N_x, N_y, N_z) = (640, 384, 640)$ in the streamwise, wall-normal and spanwise directions. The grid was stretched in the wall-normal direction but uniform in the streamwise and spanwise directions. The smallest wall-normal grid spacing was
$(N_x, N_y, N_z) = (640, 384, 640)$ in the streamwise, wall-normal and spanwise directions. The grid was stretched in the wall-normal direction but uniform in the streamwise and spanwise directions. The smallest wall-normal grid spacing was ![]() $\Delta y^{+} \approx 0.2$, where a superscript
$\Delta y^{+} \approx 0.2$, where a superscript ![]() $+$ indicates wall units.
$+$ indicates wall units.

Figure 8. Sketch of the flow domain used in the turbulent simulations. The mean flow is in the positive ![]() $x$-direction. The upper wall is smooth. Transverse grooves have been added on the lower wall, on top of a slab of the same height,
$x$-direction. The upper wall is smooth. Transverse grooves have been added on the lower wall, on top of a slab of the same height, ![]() $k$. They correspond to a solid fraction
$k$. They correspond to a solid fraction ![]() $\phi _s = 1/4$. The colours of the infusing liquid and the solid are the same as in figure 1. The external fluid is not shown.
$\phi _s = 1/4$. The colours of the infusing liquid and the solid are the same as in figure 1. The external fluid is not shown.
We placed transverse grooves with ![]() $p/k = 4$,
$p/k = 4$, ![]() $\phi _s = 1/4$ and
$\phi _s = 1/4$ and ![]() $k = 0.05H$ on the lower wall (
$k = 0.05H$ on the lower wall (![]() $-0.05H \le y \le 0$), on top of a slab of solid material with the same thickness (
$-0.05H \le y \le 0$), on top of a slab of solid material with the same thickness (![]() $-0.1H \le y \le -0.05H$). The groove height corresponds to
$-0.1H \le y \le -0.05H$). The groove height corresponds to ![]() $k^{+} \approx 9$. All wall units were based on the friction velocity of the lower surface, computed from the balance between the applied volume force in the external flow and the wall-shear stress of the smooth upper wall. The wall-unit scaled groove dimensions correspond roughly to LIS used in experiments by Fu et al. (Reference Fu, Chen, Arnold and Hultmark2019). We imposed constant temperatures
$k^{+} \approx 9$. All wall units were based on the friction velocity of the lower surface, computed from the balance between the applied volume force in the external flow and the wall-shear stress of the smooth upper wall. The wall-unit scaled groove dimensions correspond roughly to LIS used in experiments by Fu et al. (Reference Fu, Chen, Arnold and Hultmark2019). We imposed constant temperatures ![]() $T_u$ and
$T_u$ and ![]() $T_l$ at the upper and lower boundaries, respectively, similar to the laminar configuration. The viscosity ratio was set to
$T_l$ at the upper and lower boundaries, respectively, similar to the laminar configuration. The viscosity ratio was set to ![]() $\mu _i/\mu _\infty = 0.4$, corresponding roughly to heptane–water (table 1). The solid thermal conductivity was
$\mu _i/\mu _\infty = 0.4$, corresponding roughly to heptane–water (table 1). The solid thermal conductivity was ![]() $\kappa _s = \kappa _i$. We performed three simulations with Prandtl numbers
$\kappa _s = \kappa _i$. We performed three simulations with Prandtl numbers ![]() ${{Pr}}_\infty = 1$,
${{Pr}}_\infty = 1$, ![]() $2$, and
$2$, and ![]() $4$, respectively. These simulations were also conducted with smooth walls, replacing the grooves with solid material. For more information about the code and grid sensitivity studies, the reader is referred to Ciri & Leonardi (Reference Ciri and Leonardi2021), where the same code was used with a similar set-up. The results from the turbulent simulations are summarised in table 2 and will be discussed in the following subsections. Some statistics from the turbulent simulations are given in Appendix F.
$4$, respectively. These simulations were also conducted with smooth walls, replacing the grooves with solid material. For more information about the code and grid sensitivity studies, the reader is referred to Ciri & Leonardi (Reference Ciri and Leonardi2021), where the same code was used with a similar set-up. The results from the turbulent simulations are summarised in table 2 and will be discussed in the following subsections. Some statistics from the turbulent simulations are given in Appendix F.
Table 2. Summary of results from the turbulent simulations. The friction Reynolds number of the smooth channel flow was ![]() ${{Re}}_\tau ^{0} = 178.7$, and for the flow with LIS,
${{Re}}_\tau ^{0} = 178.7$, and for the flow with LIS, ![]() ${{Re}}_\tau = 176.1$, based on the friction velocity of the textured surface. The drag reduction (
${{Re}}_\tau = 176.1$, based on the friction velocity of the textured surface. The drag reduction (![]() ${{DR}}$) was computed by (5.7) and the quantities
${{DR}}$) was computed by (5.7) and the quantities ![]() $\tau ^{0}$,
$\tau ^{0}$, ![]() $q^{0}$, and
$q^{0}$, and ![]() $Nu^{0}$ are wall-shear stress, heat flux and Nusselt number of the smooth-wall simulations, respectively. The heat transfer increase has an uncertainty of
$Nu^{0}$ are wall-shear stress, heat flux and Nusselt number of the smooth-wall simulations, respectively. The heat transfer increase has an uncertainty of ![]() ${\pm }2\,\%$ (Appendix F).
${\pm }2\,\%$ (Appendix F).

5.1. Turbulent heat transfer mechanisms
All the terms in (2.5) contribute to the heat flux in a turbulent flow since the flow contains random fluctuations. The change in the heat flux can be written as
Figure 9 shows the heat flux components for smooth and liquid-infused surfaces. We observe that the contribution of the dispersive term is very small (![]() $q_{{conv,d}}/q^{0}\sim 1\,\%$) for all Prandtl numbers. Nevertheless, the total increase of the heat flux compared with the smooth-wall flow,
$q_{{conv,d}}/q^{0}\sim 1\,\%$) for all Prandtl numbers. Nevertheless, the total increase of the heat flux compared with the smooth-wall flow, ![]() $q/q^{0}$, was
$q/q^{0}$, was ![]() $3.3\,\%$,
$3.3\,\%$, ![]() $7.8\,\%$ and
$7.8\,\%$ and ![]() $14\,\%$ for
$14\,\%$ for ![]() ${{Pr}}_\infty = 1$,
${{Pr}}_\infty = 1$, ![]() $2$ and
$2$ and ![]() $4$, respectively (table 2). As shown in figure 9, for all these cases, the increase in
$4$, respectively (table 2). As shown in figure 9, for all these cases, the increase in ![]() $q_{{conv},r}/q^{0}$ dominates the change in the heat flux. However, the main reason behind the enhancement of
$q_{{conv},r}/q^{0}$ dominates the change in the heat flux. However, the main reason behind the enhancement of ![]() $q_{{conv},r}/q^{0}$ is the small but finite value of
$q_{{conv},r}/q^{0}$ is the small but finite value of ![]() $q_{{conv},d}/q$, as will be shown later in this section.
$q_{{conv},d}/q$, as will be shown later in this section.

Figure 9. Contributions to ![]() $q/q^{0}$ for the different turbulent flow cases. On this scale,
$q/q^{0}$ for the different turbulent flow cases. On this scale, ![]() $q_{{conv},d}$ is hardly visible, corresponding to approximately
$q_{{conv},d}$ is hardly visible, corresponding to approximately ![]() $1\,\%$ or less of
$1\,\%$ or less of ![]() $q$ (table 2).
$q$ (table 2).
First, however, we note that if (4.4) is valid also for turbulent flows, then the upper limit of ![]() $q_{{conv},d}/q$ for the turbulent flow set-up is
$q_{{conv},d}/q$ for the turbulent flow set-up is ![]() $2.4\,\%$. For a corresponding symmetric channel, the upper limit would be
$2.4\,\%$. For a corresponding symmetric channel, the upper limit would be ![]() $4.5\,\%$. The potential contribution from
$4.5\,\%$. The potential contribution from ![]() $q_{{conv},d}/q$ is, therefore, somewhat restricted for this set-up. Figure 10(a) shows
$q_{{conv},d}/q$ is, therefore, somewhat restricted for this set-up. Figure 10(a) shows ![]() $\rho c_p{{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}/q = {{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$ from turbulent and laminar simulations for the same Reynolds number
$\rho c_p{{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}/q = {{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$ from turbulent and laminar simulations for the same Reynolds number ![]() ${{Re}}_i = 29$. The agreement between the two systems is reasonably good and we can thus use the laminar flow to interpret the turbulent simulations. This is also corroborated by figure 10(b), where
${{Re}}_i = 29$. The agreement between the two systems is reasonably good and we can thus use the laminar flow to interpret the turbulent simulations. This is also corroborated by figure 10(b), where ![]() $q_{{conv},d}/q$ is compared with (4.3), corresponding to figure 7(a) for the laminar simulations. Indeed, earlier studies indicate that dispersive quantities of rough-wall flow can be reproduced by laminar flow if the offset of the mean velocity in the logarithmic region compared with smooth-wall flow is small (
$q_{{conv},d}/q$ is compared with (4.3), corresponding to figure 7(a) for the laminar simulations. Indeed, earlier studies indicate that dispersive quantities of rough-wall flow can be reproduced by laminar flow if the offset of the mean velocity in the logarithmic region compared with smooth-wall flow is small (![]() $\Delta U^{+} \lesssim 2$) (Abderrahaman-Elena, Fairhall & García-Mayoral Reference Abderrahaman-Elena, Fairhall and García-Mayoral2019). Correspondence between the laminar and turbulent results of
$\Delta U^{+} \lesssim 2$) (Abderrahaman-Elena, Fairhall & García-Mayoral Reference Abderrahaman-Elena, Fairhall and García-Mayoral2019). Correspondence between the laminar and turbulent results of ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$ is therefore expected here.
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$ is therefore expected here.

Figure 10. (a) Comparison of convective heat flux for LIS in laminar flow (— — —, black) and turbulent flow (— — —, ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$; ——,
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$; ——, ![]() $\left \langle v'T'\right \rangle ^{+}$;
$\left \langle v'T'\right \rangle ^{+}$; ![]() ${\cdots }\,{\cdots }$, smooth-wall reference; blue, red and yellow for
${\cdots }\,{\cdots }$, smooth-wall reference; blue, red and yellow for ![]() ${{Pr}}_\infty = 1$,
${{Pr}}_\infty = 1$, ![]() $2$ and
$2$ and ![]() $4$, respectively). For laminar and turbulent flows,
$4$, respectively). For laminar and turbulent flows, ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+} \approx 0$ in the bulk flow (
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+} \approx 0$ in the bulk flow (![]() $y > 0$), and for the turbulent flow,
$y > 0$), and for the turbulent flow, ![]() $\left \langle v'T'\right \rangle ^{+} \approx 0$ inside the grooves (
$\left \langle v'T'\right \rangle ^{+} \approx 0$ inside the grooves (![]() $y < 0$). (b) Comparison of
$y < 0$). (b) Comparison of ![]() $q_{{conv},d}/q$ from the turbulent simulations (colours as in
$q_{{conv},d}/q$ from the turbulent simulations (colours as in ![]() $a$) and (4.3) (dash-dotted line).
$a$) and (4.3) (dash-dotted line).
In the following, we rewrite (5.1) to gain a better insight into the role of the random fluctuations in the heat transfer process. The conduction term corresponds to
where ![]() ${{Nu}}^{0}$ is the Nusselt number of the smooth-wall flow. Figure 10(a) compares the convective heat flux of a smooth and LIS, where we observe only minor changes in the random component,
${{Nu}}^{0}$ is the Nusselt number of the smooth-wall flow. Figure 10(a) compares the convective heat flux of a smooth and LIS, where we observe only minor changes in the random component, ![]() $\left \langle {v'T'} \right \rangle ^{+}$. We introduce the difference in
$\left \langle {v'T'} \right \rangle ^{+}$. We introduce the difference in ![]() $q_{{conv},r}/q$ between the flow over the LIS and in the smooth channel
$q_{{conv},r}/q$ between the flow over the LIS and in the smooth channel
It follows that
using ![]() $q_{{conv},r}^{0}/q^{0} = 1 - q_{{cond}}^{0}/q^{0}$ and (5.2) in the second step. Assuming
$q_{{conv},r}^{0}/q^{0} = 1 - q_{{cond}}^{0}/q^{0}$ and (5.2) in the second step. Assuming ![]() $\epsilon = 0$, the ratio of the random convection to the total heat flux,
$\epsilon = 0$, the ratio of the random convection to the total heat flux, ![]() $q_{{conv},r}/q$, does not change for the flow over LIS compared with the smooth-wall flow. Accordingly,
$q_{{conv},r}/q$, does not change for the flow over LIS compared with the smooth-wall flow. Accordingly, ![]() $q_{{conv},r}/q^{0}$ is proportional to
$q_{{conv},r}/q^{0}$ is proportional to ![]() $q/q^{0}$.
$q/q^{0}$.
Now, using (5.2) and (5.4), (5.1) can be written as
Assuming ![]() $\epsilon = 0$, we have virtually eliminated
$\epsilon = 0$, we have virtually eliminated ![]() $q_{{conv},r}/q^{0}$ and
$q_{{conv},r}/q^{0}$ and ![]() $q_{cond}/q^{0}$ from (5.1); instead
$q_{cond}/q^{0}$ from (5.1); instead ![]() ${{Nu}}^{0}$ acts as amplification factor for
${{Nu}}^{0}$ acts as amplification factor for ![]() $q_{{conv},d}/q^{0}$. For a laminar flow
$q_{{conv},d}/q^{0}$. For a laminar flow ![]() ${{Nu}}^{0} = 1$, i.e. there is no amplification. On the other hand, if there are random fluctuations in the flow,
${{Nu}}^{0} = 1$, i.e. there is no amplification. On the other hand, if there are random fluctuations in the flow, ![]() ${{Nu}}^{0} = q_{{conv},r}^{0}/q_{cond}^{0} + 1$, demonstrating how
${{Nu}}^{0} = q_{{conv},r}^{0}/q_{cond}^{0} + 1$, demonstrating how ![]() ${{Nu}}^{0}$ increases due to convection. Hence,
${{Nu}}^{0}$ increases due to convection. Hence, ![]() ${{Nu}}^{0}$ is a measure of the amplification of
${{Nu}}^{0}$ is a measure of the amplification of ![]() $q_{{conv},d}/q^{0}$ by the random fluctuations. Indeed, this amplification can be substantial. Values measured from the simulations with smooth walls were
$q_{{conv},d}/q^{0}$ by the random fluctuations. Indeed, this amplification can be substantial. Values measured from the simulations with smooth walls were ![]() ${{Nu}}^{0} = 5.8$,
${{Nu}}^{0} = 5.8$, ![]() $7.5$ and
$7.5$ and ![]() $9.3$ for
$9.3$ for ![]() ${{Pr}}_\infty = 1, 2$ and
${{Pr}}_\infty = 1, 2$ and ![]() $4$, respectively (table 2). This effect can be expected to increase with increasing bulk Reynolds or Prandtl numbers; Kim & Lee (Reference Kim and Lee2020) noticed that
$4$, respectively (table 2). This effect can be expected to increase with increasing bulk Reynolds or Prandtl numbers; Kim & Lee (Reference Kim and Lee2020) noticed that ![]() ${{Nu}}^{0}$ increases linearly with
${{Nu}}^{0}$ increases linearly with ![]() ${{Re}}_\tau$ for a channel with smooth isothermal walls. As
${{Re}}_\tau$ for a channel with smooth isothermal walls. As ![]() $q/q^{0}$ increases due to the dispersive convection, so does
$q/q^{0}$ increases due to the dispersive convection, so does ![]() $q_{{conv},r}/q^{0}$ by (5.4).
$q_{{conv},r}/q^{0}$ by (5.4).
5.2. Predictions of heat transfer increase
By rearranging (5.5), we get an analytical expression for the change in heat flux as
 $$\begin{align} \frac{q}{q^{0}} &= \left [{1 - {{Nu}}^{0}\left(\frac{q_{{conv},d}}{q} + \epsilon\right)}\right ]^{{-}1} = \left [1 - {{Nu}}^{0}\left (\frac{q_{{conv},d}}{q}\right) \right]^{{-}1} + O(\epsilon)\nonumber\\ &= \left [{1 - \frac{q^{0}k}{\kappa_\infty (T_l - T_u)}0.11\ln({{Pe}}_i - 7.6)}\right ]^{{-}1} + O(\epsilon). \end{align}$$
$$\begin{align} \frac{q}{q^{0}} &= \left [{1 - {{Nu}}^{0}\left(\frac{q_{{conv},d}}{q} + \epsilon\right)}\right ]^{{-}1} = \left [1 - {{Nu}}^{0}\left (\frac{q_{{conv},d}}{q}\right) \right]^{{-}1} + O(\epsilon)\nonumber\\ &= \left [{1 - \frac{q^{0}k}{\kappa_\infty (T_l - T_u)}0.11\ln({{Pe}}_i - 7.6)}\right ]^{{-}1} + O(\epsilon). \end{align}$$
Here, we have performed a Taylor series expansion around ![]() $\epsilon = 0$. Equation (4.3) has been used in the latter form of the expression (applicable if
$\epsilon = 0$. Equation (4.3) has been used in the latter form of the expression (applicable if ![]() $10^{1} < {{Pe}}_i < 10^{3}$). The Nusselt number
$10^{1} < {{Pe}}_i < 10^{3}$). The Nusselt number ![]() ${{Nu}}^{0}$ (and
${{Nu}}^{0}$ (and ![]() $q^{0}$) depends on
$q^{0}$) depends on ![]() ${{Pr}}_\infty$ and
${{Pr}}_\infty$ and ![]() ${{Re}}_b$ but can be determined without performing simulations of LIS since it is a result of the smooth-wall flow. The other input parameter,
${{Re}}_b$ but can be determined without performing simulations of LIS since it is a result of the smooth-wall flow. The other input parameter, ![]() ${{Re}}_i$, can be computed or estimated using
${{Re}}_i$, can be computed or estimated using ![]() $b/p$ from figure 6(b). Therefore, if
$b/p$ from figure 6(b). Therefore, if ![]() $\epsilon$ is neglected, (5.6) predicts the heat flux of the LIS. Rastegari & Akhavan (Reference Rastegari and Akhavan2015) and Ciri & Leonardi (Reference Ciri and Leonardi2021) constructed similar relationships for drag reduction and heat transfer increase with isothermal solids, respectively.
$\epsilon$ is neglected, (5.6) predicts the heat flux of the LIS. Rastegari & Akhavan (Reference Rastegari and Akhavan2015) and Ciri & Leonardi (Reference Ciri and Leonardi2021) constructed similar relationships for drag reduction and heat transfer increase with isothermal solids, respectively.
Equation (5.6) is shown in figure 11, both for ![]() $\epsilon = 0$ and
$\epsilon = 0$ and ![]() $\epsilon = 2.3\times 10^{-3}$. The latter corresponds to the measured value for
$\epsilon = 2.3\times 10^{-3}$. The latter corresponds to the measured value for ![]() ${{Pr}}_\infty = 2$. For
${{Pr}}_\infty = 2$. For ![]() ${{Pr}}_\infty = 1$,
${{Pr}}_\infty = 1$, ![]() $\epsilon$ was somewhat lower, and for
$\epsilon$ was somewhat lower, and for ![]() ${{Pr}}_\infty = 4$ slightly higher (see table 2). The positive values of
${{Pr}}_\infty = 4$ slightly higher (see table 2). The positive values of ![]() $\epsilon$ further enhance the heat flux, which is seen from the first form of the expression in (5.6). This expression with
$\epsilon$ further enhance the heat flux, which is seen from the first form of the expression in (5.6). This expression with ![]() $\epsilon = 0$ is thus a lower limit of
$\epsilon = 0$ is thus a lower limit of ![]() $q/q^{0}$. Since the sum of
$q/q^{0}$. Since the sum of ![]() $\epsilon$ and
$\epsilon$ and ![]() $q_{{conv},d}/q$ enters the equation, their magnitudes can be compared:
$q_{{conv},d}/q$ enters the equation, their magnitudes can be compared: ![]() $q_{{conv},d}/q$ is
$q_{{conv},d}/q$ is ![]() $2.2$,
$2.2$, ![]() $3.1$ and
$3.1$ and ![]() $4.4$ times larger for
$4.4$ times larger for ![]() ${{Pr}}_\infty = 1$,
${{Pr}}_\infty = 1$, ![]() $2$ and
$2$ and ![]() $4$, respectively.
$4$, respectively.
5.3. Heat flux to drag ratio
The slight increase of ![]() $\left \langle {v'T'} \right \rangle ^{+}$ is reflected by the wall-normal velocity fluctuations. As shown in figure 12(a), the root-mean-squared value
$\left \langle {v'T'} \right \rangle ^{+}$ is reflected by the wall-normal velocity fluctuations. As shown in figure 12(a), the root-mean-squared value ![]() $v_{rms}^{+}$ increases near the surface. Such roughness effects severely reduce the drag benefits for transverse grooves (Ciri & Leonardi Reference Ciri and Leonardi2021). The LIS gave a slight drag reduction compared with the smooth wall
$v_{rms}^{+}$ increases near the surface. Such roughness effects severely reduce the drag benefits for transverse grooves (Ciri & Leonardi Reference Ciri and Leonardi2021). The LIS gave a slight drag reduction compared with the smooth wall
where ![]() $\tau$ is the total drag of the lower surface, and
$\tau$ is the total drag of the lower surface, and ![]() $\tau ^{0}$ is the wall-shear stress from the reference simulation with smooth walls. The current
$\tau ^{0}$ is the wall-shear stress from the reference simulation with smooth walls. The current ![]() ${{DR}}$ and the ideal drag reduction relationship by Rastegari & Akhavan (Reference Rastegari and Akhavan2015) are shown in figure 12(b). This relationship was derived for channels with symmetric walls but can also be applied to asymmetric configurations if
${{DR}}$ and the ideal drag reduction relationship by Rastegari & Akhavan (Reference Rastegari and Akhavan2015) are shown in figure 12(b). This relationship was derived for channels with symmetric walls but can also be applied to asymmetric configurations if ![]() ${{DR}}$ is computed by (5.7) (Fu et al. Reference Fu, Arenas, Leonardi and Hultmark2017; Ciri & Leonardi Reference Ciri and Leonardi2021). Without degrading effects, it predicts that the drag reduction would be 8 %. Nevertheless, we achieve
${{DR}}$ is computed by (5.7) (Fu et al. Reference Fu, Arenas, Leonardi and Hultmark2017; Ciri & Leonardi Reference Ciri and Leonardi2021). Without degrading effects, it predicts that the drag reduction would be 8 %. Nevertheless, we achieve ![]() ${{DR}} > 0$ together with a heat transfer increase for this geometry. Interface deformations, which have been neglected here, tend to reduce
${{DR}} > 0$ together with a heat transfer increase for this geometry. Interface deformations, which have been neglected here, tend to reduce ![]() ${{DR}}$ and increase convection further (Cartagena et al. Reference Cartagena, Arenas, Bernardini and Leonardi2018; Ciri & Leonardi Reference Ciri and Leonardi2021; Sundin, Zaleski & Bagheri Reference Sundin, Zaleski and Bagheri2021).
${{DR}}$ and increase convection further (Cartagena et al. Reference Cartagena, Arenas, Bernardini and Leonardi2018; Ciri & Leonardi Reference Ciri and Leonardi2021; Sundin, Zaleski & Bagheri Reference Sundin, Zaleski and Bagheri2021).

Figure 12. (a) The root-mean-squared wall-normal velocity for turbulent flow over LIS (——, ![]() $v_{rms}^{+}$; — — —, dispersive component
$v_{rms}^{+}$; — — —, dispersive component ![]() $v_{{rms},d}^{+}$;
$v_{{rms},d}^{+}$; ![]() $\text {---} \cdot \text {---}$, random component
$\text {---} \cdot \text {---}$, random component ![]() $v_{{rms},r}^{+}$;
$v_{{rms},r}^{+}$; ![]() ${\cdots }\,{\cdots }$, smooth-wall reference). (b) The drag reduction of the current LIS as a function of the slip length in nominal wall units (circle), compared with the ideal relation by Rastegari & Akhavan (Reference Rastegari and Akhavan2015) (solid line).
${\cdots }\,{\cdots }$, smooth-wall reference). (b) The drag reduction of the current LIS as a function of the slip length in nominal wall units (circle), compared with the ideal relation by Rastegari & Akhavan (Reference Rastegari and Akhavan2015) (solid line).

Figure 13. Grid convergence study for laminar flow with FreeFem++, with ![]() $\kappa _i = \kappa _\infty = \kappa _s$,
$\kappa _i = \kappa _\infty = \kappa _s$, ![]() $p/k = 4$,
$p/k = 4$, ![]() $\mu _i/\mu _\infty = 0.4$,
$\mu _i/\mu _\infty = 0.4$, ![]() ${{Re}}_i = 24$ and
${{Re}}_i = 24$ and ![]() ${{Pr}}_\infty = 1$ and
${{Pr}}_\infty = 1$ and ![]() $100$. Three grids were used, with
$100$. Three grids were used, with ![]() $N_y = 200$,
$N_y = 200$, ![]() $400$ and
$400$ and ![]() $800$ cells in the wall-normal direction. The horizontal scale is normalised with groove height,
$800$ cells in the wall-normal direction. The horizontal scale is normalised with groove height, ![]() $k$, and corresponds to the complete domain, with the interface at
$k$, and corresponds to the complete domain, with the interface at ![]() $y = 0$. In (b),
$y = 0$. In (b), ![]() $u_{rms}^{+}$ and
$u_{rms}^{+}$ and ![]() $v_{rms}^{+}$ denote the streamwise and wall-normal root-mean-squared velocities, respectively.
$v_{rms}^{+}$ denote the streamwise and wall-normal root-mean-squared velocities, respectively.
The heat transfer efficiency of the system can be measured by the heat flux to drag ratio or, equally, the Reynolds analogy factor, ![]() $2{{St}}/C_f$, where
$2{{St}}/C_f$, where ![]() ${{St}}$ is the Stanton number and
${{St}}$ is the Stanton number and ![]() $C_f$ is the friction coefficient. According to the Reynolds analogy,
$C_f$ is the friction coefficient. According to the Reynolds analogy, ![]() $2{{St}}/C_f = 1$ for flow over smooth walls with
$2{{St}}/C_f = 1$ for flow over smooth walls with ![]() ${{Pr}}_\infty = 1$ (Kestin & Richardson Reference Kestin and Richardson1963). Changes in the heat flux to drag ratio when introducing surface modifications at this Prandtl number thus indicate a breakage of the Reynolds analogy. A growth or a reduction equal increased or decreased heat transfer efficiency, respectively. However, the exact value of
${{Pr}}_\infty = 1$ (Kestin & Richardson Reference Kestin and Richardson1963). Changes in the heat flux to drag ratio when introducing surface modifications at this Prandtl number thus indicate a breakage of the Reynolds analogy. A growth or a reduction equal increased or decreased heat transfer efficiency, respectively. However, the exact value of ![]() $2{{St}}/C_f$ for smooth-wall flows depends on the normalisation used to form the non-dimensional numbers. The heat flux to drag ratio normalised with the smooth-wall reference values,
$2{{St}}/C_f$ for smooth-wall flows depends on the normalisation used to form the non-dimensional numbers. The heat flux to drag ratio normalised with the smooth-wall reference values, ![]() $(q/q^{0})(\tau ^{0}/\tau )$, is a valid measure of the heat transfer efficiency independently of the Prandtl number. This quantity is reported in table 2. Since both
$(q/q^{0})(\tau ^{0}/\tau )$, is a valid measure of the heat transfer efficiency independently of the Prandtl number. This quantity is reported in table 2. Since both ![]() $q/q^{0} > 1$ and
$q/q^{0} > 1$ and ![]() $\tau ^{0}/\tau > 1$ for the current set-up,
$\tau ^{0}/\tau > 1$ for the current set-up, ![]() $(q/q^{0})(\tau ^{0}/\tau )$ exceeds unity, having a maximum value of
$(q/q^{0})(\tau ^{0}/\tau )$ exceeds unity, having a maximum value of ![]() $1.17$ for
$1.17$ for ![]() ${{Pr}}_\infty = 4$. For LIS and SHS with isothermal solids, it ranges between
${{Pr}}_\infty = 4$. For LIS and SHS with isothermal solids, it ranges between ![]() $0.9$ and
$0.9$ and ![]() $1.2$ (Ciri & Leonardi Reference Ciri and Leonardi2021). Rough walls with either irregular (Forooghi, Stripf & Frohnapfel Reference Forooghi, Stripf and Frohnapfel2018) or structured textures (such as transverse bars or rods (Leonardi et al. Reference Leonardi, Orlandi, Djenidi and Antonia2015)) have been seen to reduce the Reynolds analogy factor.
$1.2$ (Ciri & Leonardi Reference Ciri and Leonardi2021). Rough walls with either irregular (Forooghi, Stripf & Frohnapfel Reference Forooghi, Stripf and Frohnapfel2018) or structured textures (such as transverse bars or rods (Leonardi et al. Reference Leonardi, Orlandi, Djenidi and Antonia2015)) have been seen to reduce the Reynolds analogy factor.
6. Conclusions
For LIS with transverse grooves, shear stress due to the external flow induces recirculation in the cavities. This recirculation increases the heat transfer by dispersive convection, contributing ![]() $q_{{conv},d}$ to the total heat flux. A net increase in the heat flux compared with a smooth surface,
$q_{{conv},d}$ to the total heat flux. A net increase in the heat flux compared with a smooth surface, ![]() $q/q^{0} > 1$, can be achieved in laminar flows if the thermal conductivity of the solid is similar to or smaller than the conductivity of infusing liquid,
$q/q^{0} > 1$, can be achieved in laminar flows if the thermal conductivity of the solid is similar to or smaller than the conductivity of infusing liquid, ![]() $\kappa _s \lesssim \kappa _i$. If
$\kappa _s \lesssim \kappa _i$. If ![]() $\kappa _s \approx \kappa _i$,
$\kappa _s \approx \kappa _i$, ![]() $q_{{conv},d}$ may be essential. Therefore, we have investigated the convection for
$q_{{conv},d}$ may be essential. Therefore, we have investigated the convection for ![]() $\kappa _s =\kappa _i$ in greater detail. The ratio
$\kappa _s =\kappa _i$ in greater detail. The ratio ![]() $q_{{conv},d}/q$ can be expressed as a function of the Péclet number based on the slip velocity and the groove height,
$q_{{conv},d}/q$ can be expressed as a function of the Péclet number based on the slip velocity and the groove height, ![]() ${{Pe}}_i$. This function resembles a logarithmic function in the interval
${{Pe}}_i$. This function resembles a logarithmic function in the interval ![]() $10^{1} < {{Pe}}_i < 10^{3}$, (4.3). The same approximation is also applicable for turbulent external flow.
$10^{1} < {{Pe}}_i < 10^{3}$, (4.3). The same approximation is also applicable for turbulent external flow.
Dispersive convection occurs only inside and in the vicinity of the surface. Therefore, apart from the dependency on ![]() ${{Pe}}_i$,
${{Pe}}_i$, ![]() $q_{{conv},d}$ is proportional to the ratio of the groove height to the total system height. This ratio is also an approximate upper limit of
$q_{{conv},d}$ is proportional to the ratio of the groove height to the total system height. This ratio is also an approximate upper limit of ![]() $q_{{conv},d}/q$ (4.4). For turbulent flows, the convection from random fluctuations in the bulk flow,
$q_{{conv},d}/q$ (4.4). For turbulent flows, the convection from random fluctuations in the bulk flow, ![]() $q_{{conv},r}$, dominates. However,
$q_{{conv},r}$, dominates. However, ![]() $q_{{conv},r}/q$ changes only slightly from the smooth-wall flow. Therefore, the dispersive convection can amplify the heat flux considerably even for turbulent flows, as expressed by (5.6).
$q_{{conv},r}/q$ changes only slightly from the smooth-wall flow. Therefore, the dispersive convection can amplify the heat flux considerably even for turbulent flows, as expressed by (5.6).
The convection in the LIS texture could be used in applications to achieve increased heat transfer. Numerous liquids can be used for LIS, whereas constraints on solid surface materials, such as weight, could limit their thermal conductivity. Low weight, for example, has been a driving force in the increased usage of micro heat exchangers (Dixit & Ghosh Reference Dixit and Ghosh2015). In addition to the increased surface heat flux, the slip induced by the LIS leads to reduced friction which lowers the required power input (Hatte & Pitchumani Reference Hatte and Pitchumani2021). These two properties make LIS augmented convective heat transfer a promising method for achieving more efficient heat exchangers.
Acknowledgements
We are thankful to U. Lācis for his help with the set up in FreeFem++.
Funding
The support of this work from SSF, the Swedish Foundation for Strategic Research (Future Leaders grant FFL15:0001), is greatly acknowledged. M. H. acknowledges the generous support from The Wenner-Gren Foundations.
Declaration of interests
The authors report no conflict of interest.
Appendix A. FIK identities
We begin with the energy equation, (2.3), and assume periodicity in the streamwise and spanwise directions. Taking the average in time and the streamwise and spanwise directions, denoted by the operator ![]() $\left \langle {} \right \rangle$,
$\left \langle {} \right \rangle$,
Integration from ![]() $-2k$, corresponding to the bottom of the domain, to
$-2k$, corresponding to the bottom of the domain, to ![]() $y$, expresses a balance between convective fluxes and conduction
$y$, expresses a balance between convective fluxes and conduction
We integrate a second time from ![]() $-2k$ to
$-2k$ to ![]() $h$
$h$
 $$\begin{align} &\rho c_p\int_{{-}2k}^{h}\left\langle {vT} \right\rangle\,\mathrm{d} y - \rho c_p\left.\left\langle {vT} \right\rangle\right|_{{-}2k}(h + 2k) \nonumber\\ &\quad -\int_{{-}2k}^{h}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y + \kappa\left.\left\langle {\frac{\partial T}{\partial y}} \right\rangle\right|_{{-}2k}(h + 2k) = 0. \end{align}$$
$$\begin{align} &\rho c_p\int_{{-}2k}^{h}\left\langle {vT} \right\rangle\,\mathrm{d} y - \rho c_p\left.\left\langle {vT} \right\rangle\right|_{{-}2k}(h + 2k) \nonumber\\ &\quad -\int_{{-}2k}^{h}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y + \kappa\left.\left\langle {\frac{\partial T}{\partial y}} \right\rangle\right|_{{-}2k}(h + 2k) = 0. \end{align}$$Identifying the heat flux at the bottom of the domain
 $$\begin{align} q &={-}\kappa\left.\left\langle {\frac{\partial T}{\partial y}} \right\rangle\right|_{{-}2k} + \rho c_p\left.\left\langle {vT} \right\rangle\right|_{{-}2k} \nonumber\\ &={-}\frac{1}{h + 2k}\int_{{-}2k}^{h}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y + \frac{\rho c_p}{h + 2k}\int_{{-}2k}^{h}\left\langle {vT} \right\rangle\,\mathrm{d} y. \end{align}$$
$$\begin{align} q &={-}\kappa\left.\left\langle {\frac{\partial T}{\partial y}} \right\rangle\right|_{{-}2k} + \rho c_p\left.\left\langle {vT} \right\rangle\right|_{{-}2k} \nonumber\\ &={-}\frac{1}{h + 2k}\int_{{-}2k}^{h}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y + \frac{\rho c_p}{h + 2k}\int_{{-}2k}^{h}\left\langle {vT} \right\rangle\,\mathrm{d} y. \end{align}$$
The integral of the conduction term can be split into an external fluid and a surface term by considering integration limits from ![]() $y = 0$ to
$y = 0$ to ![]() $h$ and
$h$ and ![]() $y = -2k$ to
$y = -2k$ to ![]() $0$, respectively. We decompose the convective flux (see Appendix B)
$0$, respectively. We decompose the convective flux (see Appendix B)
where ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$ is the dispersive component and
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}$ is the dispersive component and ![]() $\left \langle {v'T'} \right \rangle$ is the random, external flow component. This results in
$\left \langle {v'T'} \right \rangle$ is the random, external flow component. This results in
 $$\begin{align} q &={-} \frac{1}{h + 2k}\int_{0}^{h}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y - \frac{1}{h + 2k}\int_{{-}2k}^{0}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y + \frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}\left\langle {v'T'} \right\rangle\,\mathrm{d} y \nonumber\\ &\quad +\, \frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}\,\mathrm{d} y = q_{{cond},\infty} + q_{{cond},s} + q_{{cond},i} + q_{{conv},r} + q_{{conv},d}, \end{align}$$
$$\begin{align} q &={-} \frac{1}{h + 2k}\int_{0}^{h}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y - \frac{1}{h + 2k}\int_{{-}2k}^{0}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y + \frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}\left\langle {v'T'} \right\rangle\,\mathrm{d} y \nonumber\\ &\quad +\, \frac{\rho c_p}{h + 2k}\int_{{-}k}^{h}{{\left\langle\tilde{ {v} }\tilde{ {T} }\right\rangle}}\,\mathrm{d} y = q_{{cond},\infty} + q_{{cond},s} + q_{{cond},i} + q_{{conv},r} + q_{{conv},d}, \end{align}$$where conductive and convective parts have been identified. The conduction in the solid and the infusing liquid are separated after the equal sign. They can be written as
where the indicator function ![]() $\chi _s = 1$ inside the solid and
$\chi _s = 1$ inside the solid and ![]() $0$ in the liquid. The thermal conductivity
$0$ in the liquid. The thermal conductivity ![]() $\kappa$ has been identified with its value in each domain. It might therefore be moved out of the average operators and the integrals. Equation (A6) then results in (2.5).
$\kappa$ has been identified with its value in each domain. It might therefore be moved out of the average operators and the integrals. Equation (A6) then results in (2.5).
A.1. Laminar flow over a smooth wall
For a laminar flow over a smooth wall, (A1) reduces to
which means ![]() $-\left \langle {\kappa \partial T/\partial y} \right \rangle$ is constant everywhere, and equal to
$-\left \langle {\kappa \partial T/\partial y} \right \rangle$ is constant everywhere, and equal to ![]() $q$. Integrating (A9) over the solid and the external fluid
$q$. Integrating (A9) over the solid and the external fluid
respectively, where ![]() $T_l = \left \langle {T} \right \rangle |_{y=-2k}$,
$T_l = \left \langle {T} \right \rangle |_{y=-2k}$, ![]() $T_u = \left \langle {T} \right \rangle |_{y=h}$ and
$T_u = \left \langle {T} \right \rangle |_{y=h}$ and ![]() $T_s = \left \langle {T} \right \rangle |_{y=0}$. These two expressions give a solution for
$T_s = \left \langle {T} \right \rangle |_{y=0}$. These two expressions give a solution for ![]() $T_s$,
$T_s$,
Putting this expression back into (A10)
A.2. Homogeneous thermal conductivity
Simplifications of (A6) can be made by assuming ![]() $\kappa = \kappa _i = \kappa _\infty = \kappa _s$. Then
$\kappa = \kappa _i = \kappa _\infty = \kappa _s$. Then
 $$\begin{align} &- \frac{1}{h + 2k}\int_{0}^{h}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y - \frac{1}{h + 2k}\int_{{-}2k}^{0}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y \nonumber\\ &\quad = \frac{\kappa}{h + 2k}(T_s - T_u) + \frac{\kappa}{h + 2k}(T_l - T_s) = \frac{\kappa}{h + 2k}(T_l - T_u). \end{align}$$
$$\begin{align} &- \frac{1}{h + 2k}\int_{0}^{h}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y - \frac{1}{h + 2k}\int_{{-}2k}^{0}\left\langle {\kappa \frac{\partial T}{\partial y}} \right\rangle\,\mathrm{d} y \nonumber\\ &\quad = \frac{\kappa}{h + 2k}(T_s - T_u) + \frac{\kappa}{h + 2k}(T_l - T_s) = \frac{\kappa}{h + 2k}(T_l - T_u). \end{align}$$Hence
The first term is equal to (A12), as it corresponds to only the conduction.
Appendix B. Flow decomposition
For the quantity ![]() $u$
$u$
 \begin{equation} U = \left\langle {u} \right\rangle = \frac{1}{L_x L_z \Delta t}\int_0^{L_x}\int_0^{L_z}\int_{t'}^{t'+\Delta t} u(x,y,z,t) \,\mathrm{d} t \,\mathrm{d} z \,\mathrm{d} x, \end{equation}
\begin{equation} U = \left\langle {u} \right\rangle = \frac{1}{L_x L_z \Delta t}\int_0^{L_x}\int_0^{L_z}\int_{t'}^{t'+\Delta t} u(x,y,z,t) \,\mathrm{d} t \,\mathrm{d} z \,\mathrm{d} x, \end{equation}
starting averaging at some time ![]() $t'$ and over a time difference
$t'$ and over a time difference ![]() $\Delta t$. The extent of the domain in the streamwise and spanwise directions is represented by
$\Delta t$. The extent of the domain in the streamwise and spanwise directions is represented by ![]() $L_x$ and
$L_x$ and ![]() $L_z$, respectively. We may also introduce an average in time with a zero plane average,
$L_z$, respectively. We may also introduce an average in time with a zero plane average, ![]() $\tilde { {\ } }$, such that
$\tilde { {\ } }$, such that
 \begin{equation} \tilde{ {u} } = \frac{1}{\Delta t}\int_{t'}^{t'+\Delta t} u(x,y,z,t) \,\mathrm{d} t - \left\langle {u} \right\rangle, \end{equation}
\begin{equation} \tilde{ {u} } = \frac{1}{\Delta t}\int_{t'}^{t'+\Delta t} u(x,y,z,t) \,\mathrm{d} t - \left\langle {u} \right\rangle, \end{equation}giving the dispersive fluctuations. Since the transverse grooves are aligned in the spanwise direction, spatial averaging in this direction may be applied when computing these components. The periodicity of the structures can also be exploited. Using a triple decomposition (neglecting nonlinear terms, see Abderrahaman-Elena et al. Reference Abderrahaman-Elena, Fairhall and García-Mayoral2019)
where ![]() $u'$ are the random fluctuations attributed to the background turbulence. The root-mean-squared value is
$u'$ are the random fluctuations attributed to the background turbulence. The root-mean-squared value is ![]() $u_{rms} = \sqrt {\left \langle {(u-U)^{2}} \right \rangle }$. The dispersive root-mean-squared value is
$u_{rms} = \sqrt {\left \langle {(u-U)^{2}} \right \rangle }$. The dispersive root-mean-squared value is ![]() $u_{{rms},d} = \sqrt {\left \langle {\tilde { {u} }^{2}} \right \rangle }$. Also,
$u_{{rms},d} = \sqrt {\left \langle {\tilde { {u} }^{2}} \right \rangle }$. Also,
where ![]() $u_{{rms},r} = \sqrt {\left \langle {u'^{2}} \right \rangle }$. The last term is zero since there is no correlation between
$u_{{rms},r} = \sqrt {\left \langle {u'^{2}} \right \rangle }$. The last term is zero since there is no correlation between ![]() $\tilde { {u} }$ and
$\tilde { {u} }$ and ![]() $u'$. Such cross-correlations are always zero because
$u'$. Such cross-correlations are always zero because ![]() $\tilde { {u} }$ is independent of
$\tilde { {u} }$ is independent of ![]() $t$, whereas the average of
$t$, whereas the average of ![]() $u'$ in
$u'$ in ![]() $t$ is zero. Similarly, for wall-normal velocity and temperature
$t$ is zero. Similarly, for wall-normal velocity and temperature
Appendix C. Simulations with FreeFem++
The finite element solver FreeFem++ (Hecht Reference Hecht2012) was used to carry out the laminar simulations of the unit cell in two dimensions. We used a built-in tool to generate a triangle mesh with similar spacing in the streamwise and wall-normal directions, conforming to the solid boundaries and the interface. The velocities and the temperature were described by quadratic (![]() $P_2$) and the pressure by linear (
$P_2$) and the pressure by linear (![]() $P_1$) finite elements. The momentum and continuity equations were solved simultaneously in an iterative manner until convergence was reached. Afterwards, the equation for the temperature was solved.
$P_1$) finite elements. The momentum and continuity equations were solved simultaneously in an iterative manner until convergence was reached. Afterwards, the equation for the temperature was solved.
We performed a grid convergence study for ![]() $\kappa _i = \kappa _\infty = \kappa _s$,
$\kappa _i = \kappa _\infty = \kappa _s$, ![]() $p/k = 4$,
$p/k = 4$, ![]() $w/k = 3$ (
$w/k = 3$ (![]() $\phi _s = 1/4$) and
$\phi _s = 1/4$) and ![]() $\mu _i/\mu _\infty = 0.4$, corresponding to the values used in the turbulent simulations. Further,
$\mu _i/\mu _\infty = 0.4$, corresponding to the values used in the turbulent simulations. Further, ![]() ${{Re}}_\infty = 270$,
${{Re}}_\infty = 270$, ![]() ${{Re}}_i = 24$ and both
${{Re}}_i = 24$ and both ![]() ${{Pr}}_\infty = 1$ and
${{Pr}}_\infty = 1$ and ![]() $100$ were tested. The simulations were run with grids generated with
$100$ were tested. The simulations were run with grids generated with ![]() $N_y = 200$,
$N_y = 200$, ![]() $400$ and
$400$ and ![]() $800$ triangles along the wall-normal boundary. The differences in
$800$ triangles along the wall-normal boundary. The differences in ![]() $U_\infty$ and
$U_\infty$ and ![]() $q$ between the grids were less than
$q$ between the grids were less than ![]() $0.1\,\%$ for
$0.1\,\%$ for ![]() ${{Pr}}_\infty = 1$ and
${{Pr}}_\infty = 1$ and ![]() $100$. These insignificant differences show that the simulations, to a large extent, are independent of the grid. Plots of relevant quantities are shown in figure 13. Velocities are normalised with the friction velocity,
$100$. These insignificant differences show that the simulations, to a large extent, are independent of the grid. Plots of relevant quantities are shown in figure 13. Velocities are normalised with the friction velocity, ![]() $u_\tau$, temperature with
$u_\tau$, temperature with ![]() $T_l - T_u$ and
$T_l - T_u$ and ![]() $\left \langle {vT} \right \rangle$ with
$\left \langle {vT} \right \rangle$ with ![]() $q/(\rho c_p)$. The heat flux,
$q/(\rho c_p)$. The heat flux, ![]() $q$, was assessed at the top boundary. For
$q$, was assessed at the top boundary. For ![]() ${{Pr}}_\infty = 100$, there was a noticeable peak in the total heat flux at the interface, decreasing with increased resolution. It indicates the need for a fine grid to resolve the gradient in
${{Pr}}_\infty = 100$, there was a noticeable peak in the total heat flux at the interface, decreasing with increased resolution. It indicates the need for a fine grid to resolve the gradient in ![]() $\left \langle {vT} \right \rangle$ (figure 13f). However, because of the consistency in the heat flux elsewhere, all three resolutions were still considered acceptable. For the rest of the simulations, we used
$\left \langle {vT} \right \rangle$ (figure 13f). However, because of the consistency in the heat flux elsewhere, all three resolutions were still considered acceptable. For the rest of the simulations, we used ![]() $N_y = 400$.
$N_y = 400$.
Appendix D. Analytical slip length in the Stokes limit
For constant shear stress, the velocity at ![]() $y = h$ is
$y = h$ is ![]() $U_\infty = h \,\mathrm {d} U/\mathrm {d} y|_{y = 0} + U_s = (h + b)\,\mathrm {d} U/\mathrm {d} y|_{y = 0}$. Hence
$U_\infty = h \,\mathrm {d} U/\mathrm {d} y|_{y = 0} + U_s = (h + b)\,\mathrm {d} U/\mathrm {d} y|_{y = 0}$. Hence
An expression for the slip length in the Stokes limit of both longitudinal and transverse LIS was derived by Schönecker et al. (Reference Schönecker, Baier and Hardt2014). For transverse grooves, the slip length normalised by the pitch is
 \begin{equation} \frac{b}{p} = \frac{\ln\left(\cos\left(\dfrac{{\rm \pi} a}{2}\right)\right)}{2{\rm \pi} + \dfrac{\mu_i}{2aD_t(A,a)\mu_\infty}\ln\left(\dfrac{1 + \sin\left(\dfrac{{\rm \pi} a}{2}\right)}{1 - \sin\left(\dfrac{{\rm \pi} a}{2}\right)}\right)}, \end{equation}
\begin{equation} \frac{b}{p} = \frac{\ln\left(\cos\left(\dfrac{{\rm \pi} a}{2}\right)\right)}{2{\rm \pi} + \dfrac{\mu_i}{2aD_t(A,a)\mu_\infty}\ln\left(\dfrac{1 + \sin\left(\dfrac{{\rm \pi} a}{2}\right)}{1 - \sin\left(\dfrac{{\rm \pi} a}{2}\right)}\right)}, \end{equation}
where ![]() $a = w/p$ is the liquid fraction (i.e.
$a = w/p$ is the liquid fraction (i.e. ![]() $1-\phi _s$), and
$1-\phi _s$), and ![]() $D_t(A,a)$ is the maximum value of the local slip length normalised by
$D_t(A,a)$ is the maximum value of the local slip length normalised by ![]() $w$ and
$w$ and ![]() $\mu _\infty /\mu _i$, with
$\mu _\infty /\mu _i$, with ![]() $A = k/w$ here being the groove aspect ratio. It can be expressed as
$A = k/w$ here being the groove aspect ratio. It can be expressed as
where ![]() $\beta = 0.505/(2{\rm \pi} )$,
$\beta = 0.505/(2{\rm \pi} )$, ![]() $\mathrm {erf}(x)$ is the error function,
$\mathrm {erf}(x)$ is the error function,
 \begin{equation} f(a) ={-}\frac{\ln\left(\dfrac{1 + \sin\left(\dfrac{{\rm \pi} a}{2}\right)}{1 - \sin\left(\dfrac{{\rm \pi} a}{2}\right)}\right)}{2a\ln 2 \left(1 + \dfrac{2\ln\left(\cos\left(\dfrac{{\rm \pi} a}{2}\right)\right)}{2a\,\mathrm{arctanh}(a) + \ln(1 - a^{2})}\right)}, \quad \text{and} \quad g(a) = \frac{4}{\rm \pi} - \frac{4 - {\rm \pi}}{\rm \pi}a. \end{equation}
\begin{equation} f(a) ={-}\frac{\ln\left(\dfrac{1 + \sin\left(\dfrac{{\rm \pi} a}{2}\right)}{1 - \sin\left(\dfrac{{\rm \pi} a}{2}\right)}\right)}{2a\ln 2 \left(1 + \dfrac{2\ln\left(\cos\left(\dfrac{{\rm \pi} a}{2}\right)\right)}{2a\,\mathrm{arctanh}(a) + \ln(1 - a^{2})}\right)}, \quad \text{and} \quad g(a) = \frac{4}{\rm \pi} - \frac{4 - {\rm \pi}}{\rm \pi}a. \end{equation}Appendix E. Derivation of the surface Nusselt number
It is possible to derive a surface Nusselt number by considering only the surface instead of the complete domain. The average temperatures at the interface and the bottom of the texture are ![]() $T_s = \left \langle {T} \right \rangle |_{y = 0}$ and
$T_s = \left \langle {T} \right \rangle |_{y = 0}$ and ![]() $T_{lt} = \left \langle {T} \right \rangle |_{y = -k}$, respectively. We assume that
$T_{lt} = \left \langle {T} \right \rangle |_{y = -k}$, respectively. We assume that ![]() $\kappa _s = \kappa _i$ and
$\kappa _s = \kappa _i$ and
The expression (4.5) for the surface Nusselt number can be derived from the definition as follows:
 $$\begin{align} {{Nu}}_i &= \frac{kq}{\kappa_i (T_{lt} - T_s)} = \frac{k}{\kappa_i (T_{lt} - T_s)}q_{cond}\left(1 + \frac{q_{{conv},d}}{q - q_{{conv},d}}\right) \nonumber\\ &= 1 + \frac{q_{{conv},d}}{q - q_{{conv},d}} = \frac{q}{q - q_{{conv},d}} = \frac{1}{1 - q_{{conv},d}/q}. \end{align}$$
$$\begin{align} {{Nu}}_i &= \frac{kq}{\kappa_i (T_{lt} - T_s)} = \frac{k}{\kappa_i (T_{lt} - T_s)}q_{cond}\left(1 + \frac{q_{{conv},d}}{q - q_{{conv},d}}\right) \nonumber\\ &= 1 + \frac{q_{{conv},d}}{q - q_{{conv},d}} = \frac{q}{q - q_{{conv},d}} = \frac{1}{1 - q_{{conv},d}/q}. \end{align}$$Appendix F. Simulations of turbulent flow
Statistics from the turbulent simulations are shown in figure 14. The mean temperature profiles are shown as ![]() $T^{+} = (T_l - \left \langle {T} \right \rangle )\rho c_p u_\tau /q$.
$T^{+} = (T_l - \left \langle {T} \right \rangle )\rho c_p u_\tau /q$.

Figure 14. Statistics from the turbulent flow simulations (——-, LIS; ![]() ${\cdots }\,{\cdots }$, smooth-wall reference; blue, red and yellow for
${\cdots }\,{\cdots }$, smooth-wall reference; blue, red and yellow for ![]() ${{Pr}}_\infty = 1$,
${{Pr}}_\infty = 1$, ![]() $2$ and
$2$ and ![]() $4$, respectively). Wall units are based on the friction velocity of the lower wall. In (c),
$4$, respectively). Wall units are based on the friction velocity of the lower wall. In (c), ![]() $w_{rms}^{+}$ denotes the spanwise root-mean-squared velocity.
$w_{rms}^{+}$ denotes the spanwise root-mean-squared velocity.
The different contributions to the surface heat flux, ![]() $q$, for the turbulent flow simulations are shown in figure 9. For these simulations,
$q$, for the turbulent flow simulations are shown in figure 9. For these simulations, ![]() $q$ was assessed as the sum of the contributions. Deviations in the total heat flux across the channel were generally minor (approximately
$q$ was assessed as the sum of the contributions. Deviations in the total heat flux across the channel were generally minor (approximately ![]() $2\,\%$). However, at the grooves, the errors were slightly larger. The maximum deviation occurred for
$2\,\%$). However, at the grooves, the errors were slightly larger. The maximum deviation occurred for ![]() ${{Pr}}_\infty = 4$ (
${{Pr}}_\infty = 4$ (![]() $\varDelta = 0.075$, cf.
$\varDelta = 0.075$, cf. ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$ in figure 10(a) with a maximum 0.77). If
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$ in figure 10(a) with a maximum 0.77). If ![]() ${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$ is assumed to have a similar error in the grooves (i.e.
${{\left \langle \tilde { {v} }\tilde { {T} }\right \rangle }}^{+}$ is assumed to have a similar error in the grooves (i.e. ![]() $q_{conv,d}/q \pm \varDelta \cdot k/(2k + h)$), the heat transfer increase is
$q_{conv,d}/q \pm \varDelta \cdot k/(2k + h)$), the heat transfer increase is ![]() $0.12 \le q/q^{0}-1 \le 0.16$ by (5.6). Compared with the value reported in table 2, the bounds correspond to a difference of approximately
$0.12 \le q/q^{0}-1 \le 0.16$ by (5.6). Compared with the value reported in table 2, the bounds correspond to a difference of approximately ![]() $2$ percentage points, which does not affect any conclusions.
$2$ percentage points, which does not affect any conclusions.