Published online by Cambridge University Press: 11 December 2014
Direct numerical simulations (DNS) of turbulent thermal convection in a box-shaped domain with regular surface roughness at the heated bottom and cooled top surfaces are conducted for Prandtl number 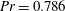 $\mathit{Pr}=0.786$ and Rayleigh numbers
$\mathit{Pr}=0.786$ and Rayleigh numbers 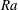 $\mathit{Ra}$ between
$\mathit{Ra}$ between 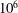 $10^{6}$ and
$10^{6}$ and 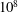 $10^{8}$. The surface roughness is introduced by four parallelepiped equidistantly distributed obstacles attached to the bottom plate, and four obstacles located symmetrically at the top plate. By varying
$10^{8}$. The surface roughness is introduced by four parallelepiped equidistantly distributed obstacles attached to the bottom plate, and four obstacles located symmetrically at the top plate. By varying 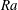 $\mathit{Ra}$ and the height and width of the obstacles, we investigate the influence of the regular wall roughness on the turbulent heat transport, measured by the Nusselt number
$\mathit{Ra}$ and the height and width of the obstacles, we investigate the influence of the regular wall roughness on the turbulent heat transport, measured by the Nusselt number 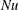 $\mathit{Nu}$. For fixed
$\mathit{Nu}$. For fixed 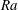 $\mathit{Ra}$, the change in the value of
$\mathit{Ra}$, the change in the value of 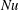 $\mathit{Nu}$ is determined not only by the covering area of the surface, i.e. the obstacle height, but also by the distance between the obstacles. The heat flux enhancement is found to be largest for wide cavities between the obstacles which can be ‘washed out’ by the flow. This is also manifested in an empirical relation, which is based on the DNS data. We further discuss theoretical limiting cases for very wide and very narrow obstacles and combine them into a simple model for the heat flux enhancement due to the wall roughness, without introducing any free parameters. This model predicts well the general trends and the order of magnitude of the heat flux enhancement obtained in the DNS. In the
$\mathit{Nu}$ is determined not only by the covering area of the surface, i.e. the obstacle height, but also by the distance between the obstacles. The heat flux enhancement is found to be largest for wide cavities between the obstacles which can be ‘washed out’ by the flow. This is also manifested in an empirical relation, which is based on the DNS data. We further discuss theoretical limiting cases for very wide and very narrow obstacles and combine them into a simple model for the heat flux enhancement due to the wall roughness, without introducing any free parameters. This model predicts well the general trends and the order of magnitude of the heat flux enhancement obtained in the DNS. In the 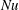 $\mathit{Nu}$ versus
$\mathit{Nu}$ versus 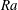 $\mathit{Ra}$ scaling, the obstacles work in two ways: for smaller
$\mathit{Ra}$ scaling, the obstacles work in two ways: for smaller 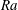 $\mathit{Ra}$ an increase of the scaling exponent compared to the smooth case is found, which is connected to the heat flux entering the cavities from below. For larger
$\mathit{Ra}$ an increase of the scaling exponent compared to the smooth case is found, which is connected to the heat flux entering the cavities from below. For larger 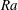 $\mathit{Ra}$ the scaling exponent saturates to the one for smooth plates, which can be understood as a full washing-out of the cavities. The latter is also investigated by considering the strength of the mean secondary flow in the cavities and its relation to the wind (i.e. the large-scale circulation), that develops in the core part of the domain. Generally, an increase in the roughness height leads to stronger flows both in the cavities and in the bulk region, while an increase in the width of the obstacles strengthens only the large-scale circulation of the fluid and weakens the secondary flows. An increase of the Rayleigh number always leads to stronger flows, both in the cavities and in the bulk.
$\mathit{Ra}$ the scaling exponent saturates to the one for smooth plates, which can be understood as a full washing-out of the cavities. The latter is also investigated by considering the strength of the mean secondary flow in the cavities and its relation to the wind (i.e. the large-scale circulation), that develops in the core part of the domain. Generally, an increase in the roughness height leads to stronger flows both in the cavities and in the bulk region, while an increase in the width of the obstacles strengthens only the large-scale circulation of the fluid and weakens the secondary flows. An increase of the Rayleigh number always leads to stronger flows, both in the cavities and in the bulk.