Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-29T19:28:38.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Head-on collisions between two quasi-geostrophic hetons in a continuously stratified fluid

Published online by Cambridge University Press:  14 August 2015

Jean N. Reinaud  and
Xavier Carton
Jean N. Reinaud*
Affiliation:
Mathematical Institute, University of St Andrews, North Haugh, St Andrews KY16 9SS, UK
Xavier Carton
Affiliation:
Laboratoire de Physique des Océans, UFR Sciences, UBO/UEB, 6 Avenue le Gorgeu, 29200 Brest, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the interactions between two three-dimensional quasi-geostrophic hetons. The hetons are initially translating towards one another. We address the effect of the vertical distance between the two poles (vortices) constituting each heton on the interaction. We also examine the influence of the horizontal separation between the poles within each heton. In this investigation, the two hetons are facing each other. Two configurations are possible depending on the respective locations of the like-signed poles of the hetons. When they lie at the same depth, we refer to the configuration as symmetric; the antisymmetric configuration corresponds to opposite-signed poles at the same depth. The first step in the investigation uses point vortices to represent the poles of the hetons. This approach allows us to rapidly browse the parameter space and to estimate the possible heton trajectories. For a symmetric pair, the hetons either reverse their trajectory or recombine and escape perpendicularly depending of their horizontal and vertical offsets. On the other hand, antisymmetric hetons recombine and escape perpendicularly as same-depth dipoles. In a second part, we focus on finite core hetons (with finite volume poles). These hetons can deform and may be sensitive to horizontal-shear-induced deformations, or to baroclinic instability. These destabilisations depend on the vertical and horizontal offsets between the various poles, as well as on their width-to-height aspect ratios. They can modify the volume of the poles via vortex merger, breaking and/or shearing out; they compete with the advective evolution observed for singular (point) vortices. Importantly, hetons can break down or reconfigure before they can drift away as expected from a point vortex approach. Thus, a large variety of behaviours is observed in the parameter space. Finally, we briefly illustrate the behaviour of tall hetons which can be unstable to an azimuthal mode 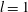$l=1$ when many vertical modes of deformation are present on the heton.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Quasi-geostrophic flows Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 779 , 25 September 2015 , pp. 144 - 180
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bambrey, R. R., Reinaud, J. N. & Dritschel, D. G. 2007 Strong interactions between two co-rotating quasi-geostrophic vortices. J. Fluid Mech. 592, 117–133.Google Scholar
Carton, X. 2001 Hydrodynamical modeling of oceanic vortices. Surv. Geophys. 22 (3), 179–263.CrossRefGoogle Scholar
Carton, X., Daniault, N., Alves, J., Chérubin, L. & Ambar, I. 2010 Meddy dynamics and interaction with neighboring eddies southwest of Portugal: observations and modeling. J. Geophys. Res. 115 (C06017), 1–23.Google Scholar
Charney, J. 1947 The dynamics of long waves in a baroclinic westerly current. J. Meteorol. 5 (5), 135–162.Google Scholar
Dritschel, D. G. 2002 Vortex merger in rotating stratified flows. J. Fluid Mech. 455, 83–101.Google Scholar
Dritschel, D. G. & de la Torre Juárez 1996 The instability and breakdown of tall columnar vortices in a quasi-geostrophic fluid. J. Fluid Mech. 328, 129–160.Google Scholar
Dritschel, D. G., Reinaud, J. N. & McKiver, W. J. 2004 The quasi-geostrophic ellipsoidal model. J. Fluid Mech. 505, 201–223.Google Scholar
Flierl, G. R. 1988 On the instability of geostrophic vortices. J. Fluid Mech. 197, 339–388.CrossRefGoogle Scholar
Gryanik, V. M. 1983 Dynamics of localized vortex perturbations on ‘vortex charges’ in a baroclinic fluid. Izv. Atmos. Ocean. Phys. 19, 347–352.Google Scholar
von Hardenberg, J., McWilliams, J. C., Provenzale, A., Shchpetkin, A. & Weiss, J. B. 2000 Vortex merging in quasi-geostrohic flows. J. Fluid Mech. 412, 331–353.Google Scholar
Haynes, P. & McIntyre, M. 1990 On the conservation and impermeability for potential vorticity. J. Atmos. Sci. 44, 828–841.Google Scholar
Helfrich, K. & Send, U. 1988 Finite-amplitude evolution of two-layer geostrophic vortices. J. Fluid Mech. 197, 331–348.Google Scholar
Hogg, N. G. & Stommel, H. M. 1985 The heton, an elementary interaction between discrete baroclinic geostrophic vortices, and its implications concerning eddy heat flow. Proc. R. Soc. Lond. A 397, 1–20.Google Scholar
L’Hegaret, P., Carton, X., Ambar, I., Menesguen, C., Hua, B., Chérubin, L., Aguiar, A., Le Cann, B., Daniault, N. & Serra, N. 2014 Evidence of Mediterranean water dipole collision in the Gulf of Cadiz. J. Geophys. Res. 119 (8), 5337–5359.Google Scholar
Ozurgurlu, E., Reinaud, J. N. & Dritschel, D. G. 2008 Interaction between two quasi-geostrophic vortices of unequal potential vorticity. J. Fluid Mech. 597, 395–414.CrossRefGoogle Scholar
Reinaud, J. N. 2015 On the stability of continuously stratified quasi-geostrophic hetons. Fluid Dyn. Res. 47, 035510.Google Scholar
Reinaud, J. N. & Carton, X. 2009 The stability and nonlinear evolution of quasi-geostrophic hetons. J. Fluid Mech. 636, 109–135.Google Scholar
Reinaud, J. N. & Dritschel, D. G. 2002 The merger of vertically offset quasi-geostrophic vortices. J. Fluid Mech. 469, 287–315.Google Scholar
Reinaud, J. N. & Dritschel, D. G. 2005 The critical merger distance between two co-rotating quasi-geostrophic vortices. J. Fluid Mech. 522, 357–381.Google Scholar
Reinaud, J. N. & Dritschel, D. G. 2009 Destructive interactions between two counter-rotating quasi-geostrophic vortices. J. Fluid Mech. 639, 195–211.Google Scholar
Sokolovskiy, M. A. 1997 Stability of an axisymmetric three-layer vortex. Izv. Atmos. Ocean. Phys. 33, 16–26.Google Scholar
Sokolovskiy, M. A. & Carton, X. 2010 Baroclinic multipole formation from heton interaction. Fluid Dyn. Res. 42, 045501.Google Scholar
Sokolovskiy, M. A. & Verron, J. 2000a Finite-core hetons: stability and interactions. J. Fluid Mech. 423, 127–154.Google Scholar
Sokolovskiy, M. A. & Verron, J. 2000b Four-vortex motion in the two layer approximation: integrable case. Regular Chaotic Dyn. 5 (4), 413–436.Google Scholar
Valcke, S. & Verron, J. 1993 On interactions between two finite-core hetons. Phys. Fluids A 5, 2058–2060.Google Scholar