Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Jinsheng
Xiao, Yue
Zhang, Linsen
Li, Mogeng
Tao, Jianjun
and
Xu, Shengjin
2020.
Extension at the downstream end of turbulent band in channel flow.
Physics of Fluids,
Vol. 32,
Issue. 12,
Song, Baofang
and
Xiao, Xiangkai
2020.
Trigger turbulent bands directly at low Reynolds numbers in channel flow using a moving-force technique.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Gomé, Sébastien
Tuckerman, Laurette S.
and
Barkley, Dwight
2020.
Statistical transition to turbulence in plane channel flow.
Physical Review Fluids,
Vol. 5,
Issue. 8,
Paranjape, Chaitanya S.
Duguet, Yohann
and
Hof, Björn
2020.
Oblique stripe solutions of channel flow.
Journal of Fluid Mechanics,
Vol. 897,
Issue. ,
Xiao, Xiangkai
and
Song, Baofang
2020.
Kinematics and Dynamics of Turbulent Bands at Low Reynolds Numbers in Channel Flow.
Entropy,
Vol. 22,
Issue. 10,
p.
1167.
Kashyap, Pavan
Duguet, Yohann
and
Dauchot, Olivier
2020.
Flow Statistics in the Transitional Regime of Plane Channel Flow.
Entropy,
Vol. 22,
Issue. 9,
p.
1001.
Klotz, L.
Pavlenko, A.M.
and
Wesfreid, J.E.
2021.
Experimental measurements in plane Couette–Poiseuille flow: dynamics of the large- and small-scale flow.
Journal of Fluid Mechanics,
Vol. 912,
Issue. ,
Liu, Chang
and
Gayme, Dennice F.
2021.
Structured input–output analysis of transitional wall-bounded flows.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Xiao, Yue
Tao, Jianjun
and
Zhang, Linsen
2021.
Self-sustaining and propagating mechanism of localized wave packet in plane-Poiseuille flow.
Physics of Fluids,
Vol. 33,
Issue. 3,
Parente, E.
Robinet, J.-Ch.
De Palma, P.
and
Cherubini, S.
2022.
Minimal energy thresholds for sustained turbulent bands in channel flow.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Wu, Haoyang
and
Song, Baofang
2022.
A numerical study of the side-wall effects on turbulent bands in channel flow at transitional Reynolds numbers.
Computers & Fluids,
Vol. 240,
Issue. ,
p.
105420.
Xu, Duo
and
Song, Baofang
2022.
Size-dependent transient nature of localized turbulence in transitional channel flow.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Gomé, Sébastien
Tuckerman, Laurette S.
and
Barkley, Dwight
2022.
Extreme events in transitional turbulence.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2226,
Matsukawa, Yuki
and
Tsukahara, Takahiro
2022.
Subcritical transition of Taylor−Couette−Poiseuille flow at high radius ratio.
Physics of Fluids,
Vol. 34,
Issue. 7,
Hof, Björn
2022.
Directed percolation and the transition to turbulence.
Nature Reviews Physics,
Vol. 5,
Issue. 1,
p.
62.
Parente, E.
Robinet, J.-Ch.
De Palma, P.
and
Cherubini, S.
2022.
Linear and nonlinear optimal growth mechanisms for generating turbulent bands.
Journal of Fluid Mechanics,
Vol. 938,
Issue. ,
Kohyama, Kazuki
Sano, Masaki
and
Tsukahara, Takahiro
2022.
Sidewall effect on turbulent band in subcritical transition of high-aspect-ratio duct flow.
Physics of Fluids,
Vol. 34,
Issue. 8,
Xiao, Yue
Zhang, Linsen
and
Tao, Jianjun
2023.
Slip boundary effect on the critical Reynolds number of subcritical transition in channel flow.
Theoretical and Applied Mechanics Letters,
Vol. 13,
Issue. 2,
p.
100431.
Zhai, Xueyan
Chen, Kaiwen
and
Song, Baofang
2023.
Linear instability of channel flow with microgroove-type anisotropic superhydrophobic walls.
Physical Review Fluids,
Vol. 8,
Issue. 2,
Paranjape, Chaitanya S.
Yalnız, Gökhan
Duguet, Yohann
Budanur, Nazmi Burak
and
Hof, Björn
2023.
Direct Path from Turbulence to Time-Periodic Solutions.
Physical Review Letters,
Vol. 131,
Issue. 3,
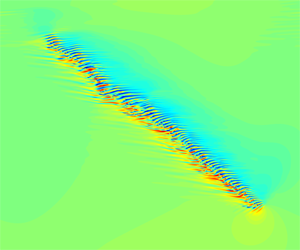
 $Re=750$. Our results show that the downstream end of the band features fast streak generation and travels into the adjacent laminar flow, whereas streaks at the upstream end decay continually and more slowly. This asymmetry is responsible for the transverse growth of the band. We particularly investigated the mechanism of streak generation at the downstream end, which drives the growth of the band. We identified a spanwise inflectional instability associated with the local mean flow near the downstream end, and our results strongly suggest that this instability is responsible for the streak generation and ultimately for the growth of the band. Based on our study, we propose a possible self-sustaining mechanism of fully localised turbulent bands at low Reynolds numbers in channel flow.
$Re=750$. Our results show that the downstream end of the band features fast streak generation and travels into the adjacent laminar flow, whereas streaks at the upstream end decay continually and more slowly. This asymmetry is responsible for the transverse growth of the band. We particularly investigated the mechanism of streak generation at the downstream end, which drives the growth of the band. We identified a spanwise inflectional instability associated with the local mean flow near the downstream end, and our results strongly suggest that this instability is responsible for the streak generation and ultimately for the growth of the band. Based on our study, we propose a possible self-sustaining mechanism of fully localised turbulent bands at low Reynolds numbers in channel flow.