Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-09T22:20:49.160Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth and spectra of gravity–capillary waves in countercurrent air/water turbulent flow

Published online by Cambridge University Press:  15 July 2015

Francesco Zonta ,
Alfredo Soldati  and
Miguel Onorato
Francesco Zonta*
Affiliation:
Department of Physics, University of Torino, Via Pietro Giuria 1, 10125 Torino, Italy Department of Electrical, Management and Mechanical Engineering, University of Udine, Via delle Scienze 208, 33100 Udine, Italy
Alfredo Soldati
Affiliation:
Department of Electrical, Management and Mechanical Engineering, University of Udine, Via delle Scienze 208, 33100 Udine, Italy Department of Fluid Mechanics, CISM, 33100 Udine, Italy
Miguel Onorato
Affiliation:
Department of Physics, University of Torino, Via Pietro Giuria 1, 10125 Torino, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

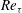Using direct numerical simulation of the Navier–Stokes equations, we analyse the dynamics of the interface between air and water when the two phases are driven by opposite pressure gradients (countercurrent configuration). The Reynolds number ($\mathit{Re}_{{\it\tau}}$), the Weber number (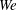$\mathit{We}$) and the Froude number (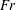$\mathit{Fr}$) fully describe the physical problem. We examine the problem of the transient growth of interface waves for different combinations of physical parameters. 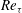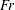Keeping $\mathit{Re}_{{\it\tau}}$ constant and varying $\mathit{We}$ and $\mathit{Fr}$, we show that, in the initial stages of the wave generation process, the amplitude of the interface elevation 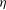${\it\eta}$ grows in time as ${\it\eta}\propto t^{2/5}$. The wavenumber spectra, 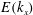$E(k_{x})$, of the surface elevation in the capillary range are in good agreement with the predictions of wave turbulence theory. Finally, the wave-induced modification of the average wind and current velocity profiles is addressed.

JFM classification

Waves/Free-surface Flows: Capillary waves Multiphase and Particle-laden Flows: Gas/liquid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 777 , 25 August 2015 , pp. 245 - 259
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartrand, T. A., Farouk, B. & Haas, C. N. 2009 Countercurrent gas/liquid flow and mixing: implications for water disinfection. Intl J. Multiphase Flow 35, 171–184.Google Scholar
Berhanu, M. & Falcon, E. 2013 Space-time-resolved capillary wave turbulence. Phys. Rev. E 87, 033003.Google Scholar
Brocchini, M. & Peregrine, D. H. 2001 The dynamics of strong turbulence at the free surface. Part 1. Description. J. Fluid Mech. 449, 225–254.Google Scholar
Cobelli, P., Przadka, A., Petitjeans, P., Lagubeau, G., Pagneux, V. & Maurel, A. 2011 Different regimes for water wave turbulence. Phys. Rev. Lett. 107, 214503.CrossRefGoogle ScholarPubMed
Deendarlianto, Hohne, T., Lucas, D. & Vierow, K. 2012 Gas liquid countercurrent two-phase flow in a PWR hot leg: a comprehensive research review. Nucl. Engng Des. 243, 214–233.Google Scholar
Deike, L., Berhanu, M. & Falcon, E. 2013 Decay of capillary wave turbulence. Phys. Rev. E 85, 066311.Google Scholar
Deike, L., Fuster, D., Berhanu, M. & Falcon, E. 2014 Direct numerical simulations of capillary wave turbulence. Phys. Rev. Lett. 112, 234501.Google Scholar
Falcon, E., Laroche, C. & Fauve, S. 2007 Observation of gravity–capillary wave turbulence. Phys. Rev. Lett. 98, 094503.Google Scholar
Fulgosi, M., Lakehal, D., Banerjee, S. & De Angelis, V. 2003 Direct numerical simulation of turbulence in a sheared air–water flow with a deformable interface. J. Fluid Mech. 482, 319–345.Google Scholar
Grare, L., Peirson, W. L., Branger, H., Walker, J. W., Giovanangeli, J. P. & Makin, V. 2013 Growth and dissipation of wind-forced deep-water waves. J. Fluid Mech. 722, 5–50.Google Scholar
Hoepffner, J., Blumenthal, R. & Zaleski, S. 2011 Self-similar wave produced by local perturbation of the Kelvin–Helmholtz shear-layer instability. Phys. Rev. Lett. 106, 104502.CrossRefGoogle ScholarPubMed
Janssen, P. A. E. M. 2004 The Interaction of Ocean Waves and Wind. Cambridge University Press.Google Scholar
Komori, S., Kurose, R., Iwano, K., Ukai, T. & Suzuki, N. 2010 Direct numerical simulation of wind-driven turbulence and scalar transfer at sheared gas–liquid interfaces. J. Turbul. 11, 1–20.Google Scholar
Lin, M., Moeng, C., Tsai, W., Sullivan, P. P. & Belcher, S. E. 2008 Direct numerical simulation of wind-wave generation processes. J. Fluid Mech. 616, 1–30.Google Scholar
Pan, Y. & Yue, D. K. P. 2014 Direct numerical investigation of turbulence of capillary waves. Phys. Rev. Lett. 113, 094501.Google Scholar
Pushkarev, A. N. & Zakharov, V. E. 1996 Turbulence of capillary waves. Phys. Rev. Lett. 76, 3320.Google Scholar
Thais, L. & Magnaudet, J. 1996 Turbulent structure beneath surface gravity waves sheared by the wind. J. Fluid Mech. 328, 313–344.Google Scholar
Wright, W. B., Budakian, R. & Putterman, S. J. 1996 Diffusing light photography of fully developed isotropic ripple turbulence. Phys. Rev. Lett. 76, 4528.Google Scholar
Zakharov, V. E., Lvov, V. S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence. Springer.CrossRefGoogle Scholar
Zonta, F., Marchioli, C. & Soldati, A. 2012a Modulation of turbulence in forced convection by temperature-dependent viscosity. J. Fluid Mech. 697, 150–174.CrossRefGoogle Scholar
Zonta, F., Onorato, M. & Soldati, A. 2012b Turbulence and internal waves in stably-stratified channel flow with temperature-dependent fluid properties. J. Fluid Mech. 697, 175–203.Google Scholar
Zonta, F. & Soldati, A. 2014 Effect of temperature dependent fluid properties on heat transfer in turbulent mixed convection. Trans. ASME J. Heat Transfer 136, 022501.Google Scholar