Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T06:25:35.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Grid turbulence in dilute polymer solutions: PEO in water

Published online by Cambridge University Press:  30 July 2013

Richard Vonlanthen  and
Peter A. Monkewitz
Richard Vonlanthen
Affiliation:
Bühler Group, CH-9240 Uzwil, Switzerland
Peter A. Monkewitz*
Affiliation:
Swiss Federal Institute of Technology (EPFL), CH-1015 Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

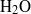Grid turbulence of polyethylene oxide (PEO) solutions (Polyox WSR-301 in ${\mathrm{H} }_{2} \mathrm{O} $) has been investigated experimentally for three concentrations of 25, 50 and 100 weight ppm, at a turbulence Reynolds number based on a Taylor microscale of 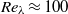${\mathit{Re}}_{\lambda } \approx 100$. For the first time, time sequences of turbulence spectra have been acquired at a rate of 0.005 Hz to reveal the spectral evolution due to mechanical degradation of the polymers. In contrast to spectra averaged over the entire degradation process, the sequence of spectra reveals a clear but time-dependent Lumley scale at which the energy spectrum changes abruptly from the Kolmogorov 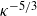${\kappa }^{- 5/ 3} $ inertial range to a 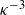${\kappa }^{- 3} $ elastic range, in which the rate of strain is maintained constant by the polymers. The scaling of the initial Lumley length with Kolmogorov dissipation rate 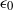${\epsilon }_{0} $ and molecular weight is determined, and a cascade model for the temporal decrease of molecular weight, i.e. for the breaking of polymer chains is presented. Finally, a heuristic model spectrum is developed which covers the cases of both maximum and partial turbulence reduction by polymers.

JFM classification

Turbulent Flows: Homogeneous turbulence Non-Newtonian Flows: Viscoelasticity
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 76 - 98
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balkovsky, E., Fouxon, A. & Lebedev, V. 2001 Turbulence of polymer solutions. Phys. Rev. E 64, 056301.Google Scholar
Barnard, B. J. S. & Sellin, R. H. J. 1969 Grid turbulence in dilute polymer solutions. Nature 222 (5199), 1160–1162.CrossRefGoogle Scholar
Benzi, R., De Angelis, E., Govindarajan, R. & Procaccia, I. 2003 Shell model for drag reduction with polymer additives in homogeneous turbulence. Phys. Rev. E 68 (1), 016308.Google Scholar
Berti, S., Bistagnino, A., Boffetta, G., Celani, A. & Musacchio, S. 2006 Small-scale statistics of viscoelastic turbulence. Europhys. Lett. 76 (1), 63–69.Google Scholar
Brostow, W. 2008 Drag reduction in flow: review of applications, mechanism and prediction. J. Ind. Engng Chem. 14 (4), 409–416.Google Scholar
De Angelis, E., Casciola, C. M., Benzi, R. & Piva, R. 2005 Homogeneous isotropic turbulence in dilute polymers. J. Fluid Mech. 531, 1–10.CrossRefGoogle Scholar
De Angelis, E., Casciola, C. M. & Piva, R. 2002 DNS of wall turbulence: dilute polymers and self-sustaining mechanisms. Comput. Fluids 31, 495–507.Google Scholar
Den Toonder, J. M. J., Draad, A. A., Kuiken, G. D. C. & Nieuwstadt, F. T. M. 1995 Degradation effects of dilute polymer-solutions on turbulent drag reduction in pipe flows. Appl. Sci. Res. 55 (1), 63–82.Google Scholar
Den Toonder, J. M. J., Hulsen, M. A., Kuiken, G. D. C. & Nieuwstadt, F. T. M. 1997 Drag reduction by polymer additives in a turbulent pipe flow: numerical and laboratory experiments. J. Fluid Mech. 337, 193–231.Google Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52 (4), 309–329.Google Scholar
Escudier, M. P., Presti, F. & Smith, S. 1999 Drag reduction in the turbulent pipe flow of polymers. J. Non-Newtonian Fluid 81 (3), 197–213.Google Scholar
Ferry, J. D. 1980 Viscoelastic Properties of Polymers, 3rd edn. Wiley.Google Scholar
Foucaut, J. M., Carlier, J. & Stanislas, M. 2004 PIV optimization for the study of turbulent flow using spectral analysis. Meas. Sci. Technol. 15, 1046–1058.Google Scholar
Fouxon, A. & Lebedev, V. 2003 Spectra of turbulence in dilute polymer solutions. Phys. Fluids 15 (7), 2060–2072.Google Scholar
Friehe, C. A. & Schwarz, W. H. 1970 Grid-generated turbulence in dilute polymer solutions. J. Fluid Mech. 44, 173–193.Google Scholar
Gadd, G. E. 1965 Turbulence damping and drag reduction produced by additives in water. Nature 206 (4983), 463–467.Google Scholar
Graessley, W. W. 1980 Polymer-chain dimensions and the dependence of viscoelastic properties on concentration, molecular-weight and solvent power. Polymer 21 (3), 258–262.Google Scholar
Groisman, A. & Steinberg, V. 2000 Elastic turbulence in a polymer solution flow. Nature 405 (6782), 53–55.Google Scholar
Groisman, A. & Steinberg, V. 2004 Elastic turbulence in curvilinear flows of polymer solutions. New J. Phys. 6, 29.Google Scholar
Hinch, E. J. 1994 Uncoiling a polymer molecule in a strong extensional flow. J. Non-Newtonian Fluid 54, 209–230.Google Scholar
Hinch, E. J. 1977 Mechanical models of dilute polymer solutions in strong flows. Phys. Fluids 20 (10), 22–30.Google Scholar
Hinch, E. J. & Elata, C. 1979 Heterogeneity of dilute polymer solutions. J. Non-Newtonian Fluid 5, 411–425.Google Scholar
Kalashnikov, V. N. & Vlasov, S. A. 1978 Scale-dependent effect in laminar-flow of dilute polymer-solution in tubes. Rheol. Acta 17 (3), 296–302.Google Scholar
Kim, K. & Sirviente, A. I. 2007 Wall versus centreline polymer injection in turbulent channel flows. Flow Turbul. Combust. 78 (1), 69–89.Google Scholar
Lavoie, P., Avallone, G., De Gregorio, F., Romano, G. P. & Antonia, R. A. 2007 Spatial resolution of PIV for the measurement of turbulence. Exp. Fluids 43 (1), 39–51.Google Scholar
Liberzon, A., Guala, M., Kinzelbach, W. & Tsinober, A. 2006 On turbulent kinetic energy production and dissipation in dilute polymer solutions. Phys. Fluids 18 (12), 125101.Google Scholar
Liberzon, A., Holzner, M., Luthi, B., Guala, M. & Kinzelbach, W. 2009 On turbulent entrainment and dissipation in dilute polymer solutions. Phys. Fluids 21 (3), 035107.Google Scholar
Lumley, J. L. 1964 Turbulence in non-Newtonian fluids. Phys. Fluids 7 (3), 335–337.Google Scholar
Lumley, J. L. 1969 Drag reduction by additives. Annu. Rev. Fluid Mech. 1, 367–384.Google Scholar
Lumley, J. L. 1973 Drag reduction in turbulent flow by polymer additives. J. Polym. Sci. Macrom. Rev. 7, 263–290.Google Scholar
McComb, W. D. 1990 The Physics of Fluid Turbulence. Oxford University Press.CrossRefGoogle Scholar
McComb, W. D., Allan, J. & Greated, C. A. 1977 Effect of polymer additives on the small-scale structure of grid-generated turbulence. Phys. Fluids 20 (6), 873–879.CrossRefGoogle Scholar
Mejia-Alvarez, R. & Christensen, K. T. 2011 Polymer-induced turbulence modifications in an impinging jet. Exp. Fluids 1–24.Google Scholar
Morgan, D. T. G. & Pike, E. W. 1972 Influence of molecular weight upon drag reduction by polymers. Rheol. Acta 11 (2), 179–184.Google Scholar
Morrison, F. A. 2001 Understanding Rheology. Oxford University Press.Google Scholar
Odell, J. A. & Keller, H. H. 1986 Flow-induced chain fracture of isolated linear macromolecules in solution. J. Polym. Sci. Part B: Polym. Phys. 24, 1889–1916.Google Scholar
Ouellette, N. T., Xu, H. & Bodenschatz, E. 2009 Bulk turbulence in dilute polymer solutions. J. Fluid Mech. 629 (1), 375–385.Google Scholar
Patterson, G. K., Zakin, J. L. & Rodrigue, J. M. 1969 Drag reduction; polymer solutions soap solutions and solid particle suspensions in pipe flows. Ind. Engng Chem. 61 (1), 22–30.CrossRefGoogle Scholar
Pipe, C. J. (2005) Experiments investigating the effects of fluid elasticity on laminar vortex shedding from a cylinder. PhD thesis, EPFL.Google Scholar
Poelma, C., Westerweel, J. & Ooms, G. 2006 Turbulence statistics from optical whole-field measurements in particle-laden turbulence. Exp. Fluids 40 (3), 347–363.Google Scholar
Pope, S. B. 2008 Turbulent Flows, 5th edn. Cambridge University Press.Google Scholar
Raffel, M., Willert, C., Wereley, S. & Kompenhans, J. 2007 Particle Image Velocimetry: a Practical Guide. Springer.CrossRefGoogle Scholar
Rodd, L. E., Cooper-White, J. J., Boger, D. V. & McKinley, G. H. 2007 Role of the elasticity number in the entry flow of dilute polymer solutions in micro-fabricated contraction geometries. J. Non-Newtonian Fluid 143 (2–3), 170–191.Google Scholar
Rozhkov, A., Prunet-Foch, B. & Vignes-Adler, M. 2003 Impact of drops of polymer solutions on small targets. Phys. Fluids 15 (7), 2006–2019.Google Scholar
Sellin, R. H. J., Hoyt, J. W., Pollert, J. & Scrivener, O. 1982 The effect of drag reducing additives on fluid-flows and their industrial applications. 2. Present applications and future proposals. J. Hydraul. Res. 20 (3), 235–292.CrossRefGoogle Scholar
Sim, H. G., Khomami, B. & Sureshkumar, R. 2007 Flow-induced chain scission in dilute polymer solutions: algorithm development and results for scission dynamics in elongational flow. J. Rheol. 51, 1223–1251.Google Scholar
Sreenivasan, K. R. & White, C. M. 2000 The onset of drag reduction by dilute polymer additives, and the maximum drag reduction asymptote. J. Fluid Mech. 409, 149–164.Google Scholar
Sureshkumar, R., Beris, A. N. & Handler, R. A. 1997 Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 9, 743–755.Google Scholar
Sylvester, N. D. & Tyler, J. S. 1970 Dilute solution properties of drag-reducing polymers. Ind. Eng. Chem. Prod. Res. Develop. 9 (4), 548–553.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Tirtaatmadja, V., McKinley, G. H. & Cooper-White, J. J. 2006 Drop formation and breakup of low viscosity elastic fluids: effects of molecular weight and concentration. Phys. Fluids 18 (4), 043101.Google Scholar
Toms, B. A. 1948 The flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of the First International Congress on Rheology, vol. 2, p. 135. North-Holland Publishing Company.Google Scholar
van Doorn, E., White, C. M. & Sreenivasan, K. R. 1999 The decay of grid turbulence in polymer and surfactant solutions. Phys. Fluids 11 (8), 2387–2393.Google Scholar
Virk, P. S. 1975 Drag reduction fundamentals. AIChE J. 21 (4), 625–656.Google Scholar
Virk, P. S., Merill, E. W., Mickley, H. S., Smith, K. A. & Mollo-Christensen, E. L. 1967 The Toms phenomenon: turbulent pipe flow of dilute polymer solutions. J. Fluid Mech. 30, 305–328.Google Scholar
Vonlanthen, R. (2010) The effects of fluid elasticity on grid turbulence. PhD thesis, EPFL.Google Scholar
Vonlanthen, R. & Monkewitz, P. A. 2011 A novel tethered-sphere add-on to enhance grid turbulence. Exp. Fluids 51, 579–585.Google Scholar
Warholic, M. D., Massah, H. & Hanratty, T. J. 1999 Influence of drag-reducing polymers on turbulence: effects of Reynolds number, concentration and mixing. Exp. Fluids 27 (5), 461–472.Google Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39 (6), 1096–1100.Google Scholar
Wyngaard, J. C. 1968 Measurement of small-scale turbulence structure with hot wires. J. Phys. E Sci. Instrum. 1 (11), 1105–1108.Google Scholar