Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-24T21:44:32.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Global vorticity shedding for a vanishing wing

Published online by Cambridge University Press:  13 February 2012

M. S. Wibawa ,
S. C. Steele ,
J. M. Dahl ,
D. E. Rival ,
G. D. Weymouth  and
M. S. Triantafyllou
M. S. Wibawa
Affiliation:
Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
S. C. Steele
Affiliation:
Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
J. M. Dahl*
Affiliation:
Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
D. E. Rival
Affiliation:
Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA Mechanical and Manufacturing Engineering, University of Calgary, 2500 University Dr NW, Calgary, AB, T2N 1N4, Canada
G. D. Weymouth
Affiliation:
Singapore–MIT Alliance for Research and Technology Centre, S16-05-08 3 Science Drive 2, 117543, Singapore
M. S. Triantafyllou
Affiliation:
Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

If a moving body were made to vanish within a fluid, its boundary-layer vorticity would be released into the fluid at all locations simultaneously, a phenomenon we call global vorticity shedding. We approximate this process by studying the related problem of rapid vorticity transfer from the boundary layer of a body undergoing a quick change of cross-sectional and surface area. 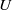A surface-piercing foil is first towed through water at constant speed, , and constant angle of attack, then rapidly pulled out of the fluid in the spanwise direction. Viewed within a fixed plane perpendicular to the span, the cross-sectional area of the foil seemingly disappears. The rapid spanwise motion results in the nearly instantaneous shedding of the boundary layer into the surrounding fluid. Particle image velocimetry measurements show that the shed layers quickly transition from free shear layers to form two strong, unequal-strength vortices, formed within non-dimensional time 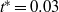, based on the foil chord and forward velocity. These vortices are connected to, and interact with, the foil’s tip vortex through additional streamwise vorticity formed during the rapid pulling of the foil. Numerical simulations show that two strong spanwise vortices form from the shed vorticity of the boundary layer. The three-dimensional effects of the foil removal process are restricted to the tip of the foil. This method of vorticity transfer may be used for quickly introducing circulation to a fluid to provide forcing for biologically inspired flow control.

JFM classification

Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex Flows Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 695 , 25 March 2012 , pp. 112 - 134
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abbott, I. H. & von Doenhoff, A. E. 1959 Theory of Wing Sections. Dover.Google Scholar
2. Alam, Md. M., Zhou, Y., Yang, H. X., Guo, H. & Mi, J. 2010 The ultra-low Reynolds number airfoil wake. Exp. Fluids 48, 81–103.CrossRefGoogle Scholar
3. Aref, H. 1983 Integrable, chaotic and turbulent vortex motion in two-dimensional flows. Annu. Rev. Fluid Mech. 15, 345–389.CrossRefGoogle Scholar
4. Betz, A. 1950 Wie Entsteht ein Wirbel in einer Wenig Zähen Flüssigkeit? Die Naturwissenschaft 37, 193–196.CrossRefGoogle Scholar
5. Birch, D. & Lee, T. 2005 Investigation of the near-field tip vortex behind an oscillating wing. J. Fluid Mech. 544, 201–241.CrossRefGoogle Scholar
6. Blondeaux, P., Fornarelli, F., Guglielmini, L., Triantafyllou, M. S. & Verzicco, R. 2005 Numerical experiments on flapping foils mimicking fish-like locomotion. Phys. Fluids 17, 113601.CrossRefGoogle Scholar
7. Buchholz, J. H. J. & Smits, A. J. 2006 On the evolution of the wake structure produced by a low-aspect-ratio pitching panel. J. Fluid Mech. 546, 433–443.CrossRefGoogle Scholar
8. Buchholz, J. H. J. & Smits, A. J. 2008 The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 603, 331–365.CrossRefGoogle ScholarPubMed
9. Childress, S., Vandenberghe, N. & Zhang, J. 2006 Hovering of a passive body in an oscillating airflow. Phys. Fluids 18, 117103.CrossRefGoogle Scholar
10. Dabiri, J. O. 2009 Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 41, 17–33.CrossRefGoogle Scholar
11. Dickinson, M. 2003 Animal locomotion: how to walk on water. Nature 424, 621–622.CrossRefGoogle ScholarPubMed
12. Dong, H., Bozkurttas, M., Mittal, R., Madden, P. & Lauder, G. V. 2010 Computational modelling and analysis of the hydrodynamics of a highly deformable fish pectoral fin. J. Fluid Mech. 645, 345–373.CrossRefGoogle Scholar
13. von Ellenrieder, K. D., Parker, K. & Soria, J. 2003 Flow structures behind a heaving and pitching finite-span wing. J. Fluid Mech. 490, 129–138.CrossRefGoogle Scholar
14. Hsieh, S. T. & Lauder, G. V. 2004 Running on water: three-dimensional force generation by basilisk lizards. Proc. Natl Acad. Sci. USA 101, 16787.CrossRefGoogle ScholarPubMed
15. Hu, D. L. & Bush, J. W. M. 2010 The hydrodynamics of water-walking arthropods. J. Fluid Mech. 644, 5–33.CrossRefGoogle Scholar
16. Hubel, T. Y., Hristov, N. I., Schwartz, S. M. & Breuer, K. S. 2009 Time-resolved wake structure and kinematics of bat flight. Exp. Fluids 46, 933–943.CrossRefGoogle Scholar
17. Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
18. Johansson, L. C. & Norberg, R. A. 2003 Delta-wing function of webbed feet gives hydrodynamic lift for swimming propulsion in birds. Nature 424, 65–68.CrossRefGoogle ScholarPubMed
19. Johansson, L. C. & Norberg, U. M. L. 2001 Lift-based paddling in diving grebe. J. Expl Biol. 204, 1687–1696.CrossRefGoogle ScholarPubMed
20. Kaden, H. 1931 Aufwicklung einer unstabilen Unstetigkeitsfläche. Ing.-Arch. 2, 140–168.CrossRefGoogle Scholar
21. Klein, F. 1910 Über die Bildung von Wirbeln in reibungslosen Flüssigkeiten. Z. Math. Phys. 58, 259–262.Google Scholar
22. Lentink, D., Müller, U. K., Stamhuis, E. J., de Kat, R., van Gestel, W., Veldhuis, L. L. M., Henningsson, P., Hedenström, A., Videler, J. J. & van Leeuwen, J. L. 2007 How swifts control their glide performance with morphing wings. Nature 446, 1082–1085.CrossRefGoogle ScholarPubMed
23. Margolin, L. G., Rider, W. J. & Grinstein, F. F. 2007 Modelling turbulent flow with implicit LES . J. Turbul. 7, 1–27.Google Scholar
24. Morton, B. R. 1984 The generation and decay of vorticity. Geophys. Astrophys. Fluid Dyn. 28, 277–308.CrossRefGoogle Scholar
25. Müller, U. K. & Lentink, D. 2004 Physiology – turning on a dime. Science 306, 1899–1900.CrossRefGoogle ScholarPubMed
26. Prandtl, L. 1927 Die Entstehung von Wirbeln in einer Flüssigkeit Kleinster Reibung. Z. Flugtech. Motorluftschiffahrt 18, 489–496.Google Scholar
27. Prandtl, L. 1936 Entstehung von Wirbeln bei Wasserströmungen: – 1. Entstehung von Wirbeln und Künstliche Beeinflussung der Wirbelbildung. Institut für Wissenschaftlichen Film (DVD) – Historische Filmaufnahmen.Google Scholar
28. Raffel, M., Willert, C. E., Wereley, S. T. & Kompenhans, J. 2007 Particle Image Velocimetry: A Practical Guide, 2nd edn. Springer.CrossRefGoogle Scholar
29. Rockwell, D. 1998 Vortex-body interactions. Annu. Rev. Fluid Mech. 30, 199–229.CrossRefGoogle Scholar
30. Slaouti, A. & Gerrard, J. H. 1981 An experimental investigation of the end effects on the wake of a circular cylinder towed through water at low Reynolds numbers. J. Fluid Mech. 112, 297–314.CrossRefGoogle Scholar
31. Spagnolie, S. E. & Shelley, M. J. 2009 Shape-changing bodies in fluid: hovering, ratcheting, and bursting. Phys. Fluids 21, 013103.CrossRefGoogle Scholar
32. Taneda, S. 1977 Visual study of unsteady separated flows around bodies. Prog. Aerosp. Sci. 17, 287–348.CrossRefGoogle Scholar
33. Taylor, G. I. 1953 Formation of a vortex ring by giving an impulse to a circular disk and then dissolving it away. J. Appl. Phys. 24, 104.CrossRefGoogle Scholar
34. Wagner, H. 1925 Über die Entstehung des dynamischen Auftriebes an Tragflügeln. Z. Angew. Math. Mech. 5, 17–35.CrossRefGoogle Scholar
35. Weymouth, G. D., Dommermuth, D. G., Hendrickson, K. & Yue, D. K.-P. 2006 Advancements in Cartesian-grid methods for computational ship hydrodynamics. In 26th Symposium on Naval Hydrodynamics. Office of Naval Research.Google Scholar
36. Weymouth, G. D. & Yue, D. K.-P. 2011 Boundary data immersion method for Cartesian-grid simulations of fluid-body interaction problems. J. Comput. Phys. 230, 6233–6247.CrossRefGoogle Scholar
37. Zdravkovich, M. M. 2003 Flow Around Circular Cylinders, Volume 2: Applications. Oxford University Press.CrossRefGoogle Scholar