Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T05:26:03.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Global stability analysis of flow through a fusiform aneurysm: steady flows

Published online by Cambridge University Press:  02 July 2014

Shyam Sunder Gopalakrishnan ,
Benoît Pier  and
Arie Biesheuvel
Shyam Sunder Gopalakrishnan*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS – École Centrale de Lyon, Université Claude-Bernard Lyon 1, INSA de Lyon, 36 Avenue Guy de Collongue, 69134 Écully, France
Benoît Pier
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS – École Centrale de Lyon, Université Claude-Bernard Lyon 1, INSA de Lyon, 36 Avenue Guy de Collongue, 69134 Écully, France
Arie Biesheuvel
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS – École Centrale de Lyon, Université Claude-Bernard Lyon 1, INSA de Lyon, 36 Avenue Guy de Collongue, 69134 Écully, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The global linear stability of steady axisymmetric flow through a model fusiform aneurysm is studied numerically. The aneurysm is modelled as a Gaussian-shaped inflation on a vessel of circular cross-section. The fluid is assumed to be Newtonian, and the flow far upstream and downstream of the inflation is a Hagen–Poiseuille flow. The model aneurysm is characterized by a maximum height 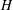$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H$ and width 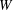$W$, non-dimensionalized by the upstream vessel diameter, and the steady flow is characterized by the Reynolds number of the upstream flow. The base flow through the model aneurysms is determined for non-dimensional heights and widths in the physiologically relevant ranges 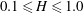$0.1 \leq H \leq 1.0$ and 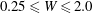$0.25 \leq W \leq 2.0$, and for Reynolds numbers up to 7000, corresponding to peak values recorded during pulsatile flows under physiological conditions. It is found that the base flow consists of a core of relatively fast-moving fluid, surrounded by a slowly recirculating fluid that fills the inflation; for larger values of the ratio 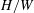$H/W$, a secondary recirculation region is observed. The wall shear stress (WSS) in the inflation is vanishingly small compared to the WSS in the straight vessels. The global linear stability of the base flows is analysed by determining the eigenfrequencies of a modal representation of small-amplitude perturbations and by looking at the energy transfer between the base flow and the perturbations. Relatively shallow aneurysms (of relatively large width) become unstable by the lift-up mechanism and have a perturbation flow which is characterized by stationary, growing modes. More localized aneurysms (with relatively small width) become unstable at larger Reynolds numbers, presumably by an elliptic instability mechanism; in this case the perturbation flow is characterized by oscillatory modes.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 90 - 106
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackburn, H. M. & Sherwin, S. J. 2007 Instability modes and transition of pulsatile stenotic flow: pulse-period dependence. J. Fluid Mech. 573, 57–88.CrossRefGoogle Scholar
Blackburn, H. M., Sherwin, S. J. & Barkley, D. 2008 Convective instability and transient growth in steady and pulsatile stenotic flows. J. Fluid Mech. 607, 267–277.Google Scholar
Bluestein, D., Niu, L., Schoephoerster, R. T. & Dewanjee, M. K. 1996 Steady flow in an aneurysm model: correlation between fluid dynamics and blood platelet deposition. Trans. ASME: J. Biomed. Engng 118, 280–286.Google Scholar
Boiron, O., Deplano, V. & Pelissier, R. 2007 Experimental and numerical studies on the starting effect on the secondary flow in a bend. J. Fluid Mech. 574, 109–129.CrossRefGoogle Scholar
Budwig, R., Elger, D., Hooper, H. & Slippy, J. 1993 Steady flow in abdominal aortic aneurysm models. Trans. AMSE: J. Biomed. Engng 115, 418–423.Google ScholarPubMed
Ehrenstein, U. & Gallaire, F. 2005 On two-dimensional temporal modes in spatially evolving open flows: the flat-plate boundary layer. J. Fluid Mech. 536, 221–233.Google Scholar
Finol, E. A. & Amon, C. H. 2001 Blood flow in abdominal aortic aneurysms: pulsatile flow haemodynamics. Trans. ASME: J. Biomech. Engng 123, 474–484.Google Scholar
Finol, E. A. & Amon, C. H. 2002a Flow-induced wall shear stress in abdominal aortic aneurysm: part I – steady flow haemodynamics. Comput. Meth. Biomech. Biomed. Engng 5, 309–318.Google Scholar
Finol, E. A. & Amon, C. H. 2002b Flow-induced wall shear stress in abdominal aortic aneurysm: part II – pulsatile flow haemodynamics. Comput. Meth. Biomech. Biomed. Engng 5, 319–328.CrossRefGoogle Scholar
Gopalakrishnan, S. S.2014 Dynamics and stability of flow through an abdominal aortic aneurysm. PhD thesis, Université de Lyon, http://hal.archives-ouvertes.fr/tel-00954202.Google Scholar
Griffith, M. D., Leweke, T., Thompson, M. C. & Hourigan, K. 2008 Steady inlet flow in stenotic geometries: convective and absolute instabilities. J. Fluid Mech. 616, 111–133.Google Scholar
Griffith, M. D., Leweke, T., Thompson, M. C. & Hourigan, K. 2009 Pulsatile flow in stenotic geometries: flow behaviour and stability. J. Fluid Mech. 622, 291–320.Google Scholar
Griffith, M. D., Leweke, T., Thompson, M. C. & Hourigan, K. 2013 Effect of small asymmetries on axisymmetric stenotic flow. J. Fluid Mech. 721, R1.Google Scholar
Griffith, M. D., Thompson, M. C., Leweke, T., Hourigan, K. & Anderson, W. P. 2007 Wake behaviour and instability of flow through a partially blocked channel. J. Fluid Mech. 582, 319–340.Google Scholar
Humphrey, J. D. & Taylor, C. A. 2008 Intracranial and abdominal aortic aneurysms: similarities, differences, and need for a new class of computational models. Annu. Rev. Biomed. Engng 10, 221–246.Google Scholar
Ku, D. N. 1997 Blood flow in arteries. Annu. Rev. Fluid Mech. 29, 399–434.CrossRefGoogle Scholar
Lanzerstorfer, D. & Kuhlmann, H. C. 2012 Global stability of the two-dimensional flow over a backward-facing step. J. Fluid Mech. 693, 1–27.Google Scholar
Lasheras, J. C. 2007 The biomechanics of arterial aneurysms. Annu. Rev. Fluid Mech. 39, 293–319.Google Scholar
Mao, X., Sherwin, S. J. & Blackburn, H. M. 2011 Transient growth and bypass transition in stenotic flow with a physiological waveform. Theor. Comput. Fluid Dyn. 25, 31–42.Google Scholar
Marquet, O., Lombardi, M., Chomaz, J. M., Sipp, D. & Jacquin, L. 2009 Direct and adjoint global modes of a recirculation bubble. J. Fluid Mech. 622, 1–21.CrossRefGoogle Scholar
Nayar, N. & Ortega, J. M. 1993 Computation of selected eignevalues of generalized eigenvalue problems. J. Comput. Phys. 108, 8–14.Google Scholar
Nerem, R. M., Seed, W. A. & Wood, N. B. 1972 An experimental study of the velocity distribution and transition to turbulence in the aorta. J. Fluid Mech. 52, 137–160.Google Scholar
Peattie, R. A., Asbury, C. L., Bluth, E. I. & Ruberti, J. W. 1996 Steady flow in models of abdominal aortic aneurysms. Part I: investigation of the velocity patterns. J. Ultrasound Med. 15, 679–688.Google Scholar
Peattie, R. A., Schrader, T., Bluth, E. I. & Comstock, C. E. 1994 Development of turbulence in steady flow through models of abdominal aortic aneurysms. J. Ultrasound Med. 13, 467–472.Google Scholar
Peterson, S. D. & Plesniak, M. 2008 The influence of inlet velocity profile and secondary flow on pulsatile flow in a model artery with stenosis. J. Fluid Mech. 616, 263–301.CrossRefGoogle Scholar
Salsac, A.-V., Sparks, S. R., Chomaz, J.-M. & Lasheras, J. C. 2006 Evolution of the wall shear stresses during the progressive enlargement of symmetric abdominal aortic aneurysms. J. Fluid Mech. 560, 19–51.CrossRefGoogle Scholar
Sheard, G. J. 2009 Flow dynamics and wall shear stress variation in a fusiform aneurysm. J. Engng Maths 64, 379–390.Google Scholar
Sherwin, S. J. & Blackburn, H. M. 2005 Three-dimensional instabilities and transition of steady and pulsatile axisymmetric stenotic flows. J. Fluid Mech. 533, 297–327.Google Scholar
Shortis, T. A. & Hall, P. 1999 On the nonlinear stability of the oscillatory viscous flow of an incompressible fluid in a curved pipe. J. Fluid Mech. 379, 145–163.Google Scholar
Sorensen, D. C. 1992 Implicit application of polynomial filters in a $k$ -step Arnoldi method. SIAM J. Matrix Anal. Applics. 13, 357–385.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.Google Scholar
Trip, R., Kuik, D. J., Westerweel, J. & Poelma, C. 2012 An experimental study of transitional pulsatile pipe flow. Phys. Fluids 24, 014103.Google Scholar
Vétel, J., Garon, A., Pelletier, D. & Farinas, M. I. 2008 Asymmetry and transition to turbulence in a smooth axisymmetric constriction. J. Fluid Mech. 607, 351–386.Google Scholar
Yip, T. H. & Yu, S. C. M. 2001 Cyclic transition to turbulence in rigid abdominal aortic aneurysm models. Fluid Dyn. Res. 29, 81–113.CrossRefGoogle Scholar