Published online by Cambridge University Press: 01 August 2016
Statistical properties of turbulent Rayleigh–Bénard convection at low Prandtl numbers 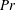 $Pr$, which are typical for liquid metals such as mercury or gallium (
$Pr$, which are typical for liquid metals such as mercury or gallium (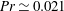 $Pr\simeq 0.021$) or liquid sodium (
$Pr\simeq 0.021$) or liquid sodium (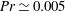 $Pr\simeq 0.005$), are investigated in high-resolution three-dimensional spectral element simulations in a closed cylindrical cell with an aspect ratio of one and are compared to previous turbulent convection simulations in air for
$Pr\simeq 0.005$), are investigated in high-resolution three-dimensional spectral element simulations in a closed cylindrical cell with an aspect ratio of one and are compared to previous turbulent convection simulations in air for 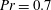 $Pr=0.7$. We compare the scaling of global momentum and heat transfer. The scaling exponent
$Pr=0.7$. We compare the scaling of global momentum and heat transfer. The scaling exponent 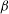 $\unicode[STIX]{x1D6FD}$ of the power law
$\unicode[STIX]{x1D6FD}$ of the power law 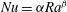 $Nu=\unicode[STIX]{x1D6FC}Ra^{\unicode[STIX]{x1D6FD}}$ is
$Nu=\unicode[STIX]{x1D6FC}Ra^{\unicode[STIX]{x1D6FD}}$ is 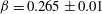 $\unicode[STIX]{x1D6FD}=0.265\pm 0.01$ for
$\unicode[STIX]{x1D6FD}=0.265\pm 0.01$ for 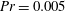 $Pr=0.005$ and
$Pr=0.005$ and 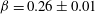 $\unicode[STIX]{x1D6FD}=0.26\pm 0.01$ for
$\unicode[STIX]{x1D6FD}=0.26\pm 0.01$ for 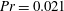 $Pr=0.021$, which are smaller than that for convection in air (
$Pr=0.021$, which are smaller than that for convection in air (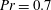 $Pr=0.7$,
$Pr=0.7$, 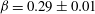 $\unicode[STIX]{x1D6FD}=0.29\pm 0.01$). These exponents are in agreement with experiments. Mean profiles of the root-mean-square velocity as well as the thermal and kinetic energy dissipation rates have growing amplitudes with decreasing Prandtl number, which underlies a more vigorous bulk turbulence in the low-
$\unicode[STIX]{x1D6FD}=0.29\pm 0.01$). These exponents are in agreement with experiments. Mean profiles of the root-mean-square velocity as well as the thermal and kinetic energy dissipation rates have growing amplitudes with decreasing Prandtl number, which underlies a more vigorous bulk turbulence in the low-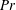 $Pr$ regime. The skin-friction coefficient displays a Reynolds number dependence that is close to that of an isothermal, intermittently turbulent velocity boundary layer. The thermal boundary layer thicknesses are larger as
$Pr$ regime. The skin-friction coefficient displays a Reynolds number dependence that is close to that of an isothermal, intermittently turbulent velocity boundary layer. The thermal boundary layer thicknesses are larger as 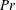 $Pr$ decreases and conversely the velocity boundary layer thicknesses become smaller. We investigate the scaling exponents and find a slight decrease in exponent magnitude for the thermal boundary layer thickness as
$Pr$ decreases and conversely the velocity boundary layer thicknesses become smaller. We investigate the scaling exponents and find a slight decrease in exponent magnitude for the thermal boundary layer thickness as 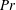 $Pr$ decreases, but find the opposite case for the velocity boundary layer thickness scaling. A growing area fraction of turbulent patches close to the heating and cooling plates can be detected by exceeding a locally defined shear Reynolds number threshold. This area fraction is larger for lower
$Pr$ decreases, but find the opposite case for the velocity boundary layer thickness scaling. A growing area fraction of turbulent patches close to the heating and cooling plates can be detected by exceeding a locally defined shear Reynolds number threshold. This area fraction is larger for lower 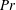 $Pr$ at the same
$Pr$ at the same 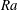 $Ra$, but the scaling exponent of its growth with Rayleigh number is reduced. Our analysis of the kurtosis of the locally defined shear Reynolds number demonstrates that the intermittency in the boundary layer is significantly increased for the lower Prandtl number and for sufficiently high Rayleigh number compared to convection in air. This complements our previous findings of enhanced bulk intermittency in low-Prandtl-number convection.
$Ra$, but the scaling exponent of its growth with Rayleigh number is reduced. Our analysis of the kurtosis of the locally defined shear Reynolds number demonstrates that the intermittency in the boundary layer is significantly increased for the lower Prandtl number and for sufficiently high Rayleigh number compared to convection in air. This complements our previous findings of enhanced bulk intermittency in low-Prandtl-number convection.