Published online by Cambridge University Press: 15 June 2017
Convection in a rotating rectangular basin with differential thermal forcing at one horizontal boundary is examined using laboratory experiments. The experiments have an imposed heat flux boundary condition, are at large values of the flux Rayleigh number (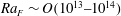 $Ra_{F}\sim O(10^{13}{-}10^{14})$ based on the box length
$Ra_{F}\sim O(10^{13}{-}10^{14})$ based on the box length 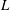 $L$), use water with Prandtl number
$L$), use water with Prandtl number 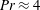 $Pr\approx 4$ and have a small depth to length aspect ratio. The results show the conditions for transition from non-rotating horizontal convection governed by an inertial–buoyancy balance in the thermal boundary layer, to circulation governed by geostrophic flow in the boundary layer. The geostrophic balance constrains mean flow and reduces the heat transport as Nusselt number
$Pr\approx 4$ and have a small depth to length aspect ratio. The results show the conditions for transition from non-rotating horizontal convection governed by an inertial–buoyancy balance in the thermal boundary layer, to circulation governed by geostrophic flow in the boundary layer. The geostrophic balance constrains mean flow and reduces the heat transport as Nusselt number 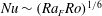 $Nu\sim (Ra_{F}Ro)^{1/6}$, where
$Nu\sim (Ra_{F}Ro)^{1/6}$, where  $Ro=B^{1/2}/f^{3/2}L$ is the convective Rossby number,
$Ro=B^{1/2}/f^{3/2}L$ is the convective Rossby number, 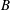 $B$ is the imposed buoyancy flux and
$B$ is the imposed buoyancy flux and 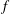 $f$ is the Coriolis parameter. Thus flow in the geostrophic boundary layer regime is governed by the relative roles of horizontal convective accelerations and Coriolis accelerations, or buoyancy and rotation, in the boundary layer. Experimental evidence suggests that for more rapid rotation there is another transition to a regime in which the momentum budget is dominated by fluctuating vertical accelerations in a region of vortical plumes, which we refer to as a ‘chimney’ following related discussion of regions of deep convection in the ocean. Coupling of the chimney convection in the region of destabilising boundary flux to the diffusive boundary layer of horizontal convection in the region of stabilising boundary flux gives heat transport independent of rotation in this ‘inertial chimney’ regime, and the new scaling
$f$ is the Coriolis parameter. Thus flow in the geostrophic boundary layer regime is governed by the relative roles of horizontal convective accelerations and Coriolis accelerations, or buoyancy and rotation, in the boundary layer. Experimental evidence suggests that for more rapid rotation there is another transition to a regime in which the momentum budget is dominated by fluctuating vertical accelerations in a region of vortical plumes, which we refer to as a ‘chimney’ following related discussion of regions of deep convection in the ocean. Coupling of the chimney convection in the region of destabilising boundary flux to the diffusive boundary layer of horizontal convection in the region of stabilising boundary flux gives heat transport independent of rotation in this ‘inertial chimney’ regime, and the new scaling 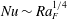 $Nu\sim Ra_{F}^{1/4}$. Scaling analysis predicts the transition conditions observed in the experiments, as well as a further ‘geostrophic chimney’ regime in which the vertical plumes are controlled by local geostrophy. When
$Nu\sim Ra_{F}^{1/4}$. Scaling analysis predicts the transition conditions observed in the experiments, as well as a further ‘geostrophic chimney’ regime in which the vertical plumes are controlled by local geostrophy. When 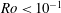 $Ro<10^{-1}$, the convection is also observed to produce a set of large basin-scale gyres at all depths in the time-averaged flow.
$Ro<10^{-1}$, the convection is also observed to produce a set of large basin-scale gyres at all depths in the time-averaged flow.