Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T16:57:01.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry and interaction of structures in homogeneous isotropic turbulence

Published online by Cambridge University Press:  29 August 2012

T. Leung ,
N. Swaminathan  and
P. A. Davidson
T. Leung
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
N. Swaminathan*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
P. A. Davidson
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A strategy to extract turbulence structures from direct numerical simulation (DNS) data is described along with a systematic analysis of geometry and spatial distribution of the educed structures. A DNS dataset of decaying homogeneous isotropic turbulence at Reynolds number 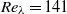is considered. A bandpass filtering procedure is shown to be effective in extracting enstrophy and dissipation structures with their smallest scales matching the filter width, . The geometry of these educed structures is characterized and classified through the use of two non-dimensional quantities, ‘planarity’ and ‘filamentarity’, obtained using the Minkowski functionals. The planarity increases gradually by a small amount as is decreased, and its narrow variation suggests a nearly circular cross-section for the educed structures. The filamentarity increases significantly as decreases demonstrating that the educed structures become progressively more tubular. An analysis of the preferential alignment between the filtered strain and vorticity fields reveals that vortical structures of a given scale 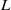are most likely to align with the largest extensional strain at a scale 3–5 times larger than 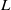. This is consistent with the classical energy cascade picture, in which vortices of a given scale are stretched by and absorb energy from structures of a somewhat larger scale. The spatial distribution of the educed structures shows that the enstrophy structures at the 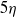scale (where 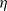is the Kolmogorov scale) are more concentrated near the ones that are 3–5 times larger, which gives further support to the classical picture. Finally, it is shown by analysing the volume fraction of the educed enstrophy structures that there is a tendency for them to cluster around a larger structure or clusters of larger structures.

JFM classification

Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 453 - 481
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ashurst, Wm. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30, 2343–2353.CrossRefGoogle Scholar
2. Bermejo-Moreno, I. & Pullin, D. I. 2008 On the nonlocal geometry of turbulence. J. Fluid Mech. 603, 101–135.CrossRefGoogle Scholar
3. Bermejo-Moreno, I., Pullin, D. I. & Horiuti, K. 2009 Geometry of enstrophy and dissipation, grid resolution effects and proximity issues in turbulence. J. Fluid Mech. 620, 121–166.CrossRefGoogle Scholar
4. Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1, 497–504.CrossRefGoogle Scholar
5. Einasto, M., Saar, E., Liivamägi, L. J., Einasto, J., Tago, E., Martínez, V. J., Starck, J.-L., Müller, V., Heinämäki, P., Nrmi, P., gramann, M. & Hütsi, G. 2007 The richest superclusters. i. Morphology. Astron. Astrophys. 476, 697–711.CrossRefGoogle Scholar
6. Goto, S. 2008 A physical mechanism of the energy cascade in homogeneous isotropic turbulence. J. Fluid Mech. 605, 355–366.CrossRefGoogle Scholar
7. Goto, S. & Kida, S. 2003 A physical mechanism of the energy cascade in homogeneous isotropic turbulence. Fluid Dyn. Res. 33, 403–431.Google Scholar
8. Hadwiger, H. 1957 Vorlesungen über Inhalt, Oberfläache und Isoperimetrie. Springer.CrossRefGoogle Scholar
9. Hamlington, P. E., Schumacher, J. & Dahm, W. J. A. 2008 Local and nonlocal strain rate fields and vorticity alignmnet in turbulent flows. Phys. Rev. E 77, 1–6.Google Scholar
10. Horiuti, K. 2001 A classification method for vortex sheet and tube structures in turbulent flows. Phys. Fluids 13, 3756–3774.CrossRefGoogle Scholar
11. Horiuti, K. & Takagi, Y. 2005 Identification method for vortex sheet structures in turbulent flows. Phys. Fluids 17, 121703.CrossRefGoogle Scholar
12. Hosokawa, I. & Yamamoto, K. 1990 Intermittency of dissipation in directly simulated fully developed turbulence. J. Phys. Soc. Japan 59, 401404.CrossRefGoogle Scholar
13. Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, stream, convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research, Stanford, CA, USA.Google Scholar
14. Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
15. Jiménez, J. 1992 Kinematic alignment effects in turbulent flows. Phys. Fluids A 4, 652–654.CrossRefGoogle Scholar
16. Jiménez, J. 1994 Columnar vortices in isotropic turbulence. Meccanica 29, 453–464.CrossRefGoogle Scholar
17. Jiménez, J. & Wray, A. A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.CrossRefGoogle Scholar
18. Jiménez, J., Wray, A. A., Saffman, P. & Rogallo, R. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
19. Kerscher, M., Schmalzing, J., Retzlaff, J., Borgani, S., Buchert, T., Gottlöber, S., Müller, V., Plionis, M. & Wagner, H. 1997 Minkowski functionals of abell/aco clusters. Mon. Not. R. Astron. Soc. 284, 73–84.Google Scholar
20. Mecke, K. R., Buchert, T. & Wagner, H. 1994 Robust morphological measures for large-scales structures in the universe. Astron. Astrophys. 288, 697–704.Google Scholar
21. Meyer, M., Desbrun, M., Schroder, P. & Barr, A. H. 2002 Discrete differential-geometry operators for triangulared 2-manifolds. Tech. Rep. Caltech. http://www.multires.caltech.edu/pubs/difGeoOps.pdf.CrossRefGoogle Scholar
22. Michielsen, K. & Raedt, H. De 2001 Integral-geometry morphological image analysis. Phys. Rep. 347, 461–538.CrossRefGoogle Scholar
23. Moisy, F. & Jimenez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.CrossRefGoogle Scholar
24. Nomura, K. K. & Post, G. K. 1998 The structure and dynamics of vorticity and rate of strain in incompressible homogeneous turbulence. J. Fluid Mech. 377, 65–97.CrossRefGoogle Scholar
25. Ohkitani, K. 2002 Numerial study of comparison of vorticity and passive vectors in turbulence and inviscid flows. Phys. Rev. E 65, 046304.CrossRefGoogle Scholar
26. Passot, T., Politano, H., Sulem, P. L., Angilella, J. R. & Meneguzzi, M. 1995 Instability of strained vortex layers and vortex tube formation in homogeneous turbulence. J. Fluid Mech. 282, 313–338.CrossRefGoogle Scholar
27. Ruetsch, G. R. & Maxey, M. R. 1994 Small-scale features of vorticity and passive scalar fields in homogeneous isotropic turbulence. Phys. Fluids A 3, 1587–1597.CrossRefGoogle Scholar
28. Sahni, V., Sathyaprakash, B. S. & Shandarin, S. F. 1998 Shapefinders: a new shap diagnostic for large-scale structure. Astrophys. J. 495, L5–L8.CrossRefGoogle Scholar
29. Schmalzing, J. & Buchert, T. 1997 Beyond genus statistics: a unifying approach to the morphology of cosmic structure. Astrophys. J. 482, L1–L4.CrossRefGoogle Scholar
30. Schmalzing, J., Buchert, T., Melott, A. L., Sahni, V., Sathyaprakash, B. S. & Shandarin, S. F. 1999 Disentangling the cosmic web I. Morphology of isodensity contours. Astrophys. J. 526, 568–578.CrossRefGoogle Scholar
31. Shandarin, S. F., Sheth, J. V. & Sahni, V. 2004 Morphology of the supercluster-void network in cosmology. Mon. Not. R. Astron. Soc. 353, 162–178.Google Scholar
32. She, Z.-S., Jackson, E. & Orszag, S. A. 1991 Structure and dynamics of homogeneous turbulence: models and simulations. Proc. R. Soc. Lond. A 434, 101–124.Google Scholar
33. Sheth, J. V. & Sahni, V. 2005 Exploring the geometry topology and morpholgy of large scale structure using Minkowski functionals. Curr. Sci. 1101–1116, 568–578.Google Scholar
34. Sheth, J. V., Shandarin, S. F. & Sathyaprakash, B. S. 2003 Measuring the geometry and topology of large-scale structure using SURFGEN: methodology and preliminary results. Mon. Not. R. Astron. Soc. 343, 22–46.Google Scholar
35. Siggia, E. D. 1981 Numerical study of small-scale intermittency in three-dimensional turbulence. J. Fluid Mech. 107, 375–406.CrossRefGoogle Scholar
36. Tanahashi, M., Miyauchi, M. & Ikeda, J. 1999 Fine scale structure in turbulence, fluid mechanics and its application. In Simulation and Identification of Organized Structures in Flows, Fluid Mechanics and its Applications. IUTAM Symposium, vol. 52, pp. 131–140. IUTAM.Google Scholar
37. Tennekes, A. A. 1968 Simple model for the small-scale structure of turbulence. Phys. Fluids 11, 669–670.CrossRefGoogle Scholar
38. Thompson, A. C. 1996 Minkowski Geometry. Cambridge University Press.CrossRefGoogle Scholar
39. Townsend, A. A. 1951 On the fine-scale structure of turbulence. Proc. R. Soc. Lond. A 208, 534–542.Google Scholar
40. Vieillefosse, P. 1982 Local interaction between vorticity and shear in a perfect incompressible fluid. J. Phys. Paris 43, 837–842.Google Scholar
41. Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.CrossRefGoogle Scholar
42. Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.CrossRefGoogle Scholar
43. Wilkin, S. L., Barenghi, C. F. & Shukurov, A. 2007 Magnetic structures produced by the small-scale dynamo. Phys. Rev. Lett. 99, 134501.CrossRefGoogle ScholarPubMed
44. Worth, N. 2010 Tomographic-PIV measurement of coherent dissipation scale structures. PhD thesis, University of Cambridge, Cambridge.Google Scholar
45. Yang, Y. & Pullin, D. I. 2011 Geometric study of Lagrangian and Eulerian structures in turbulent channel flow. J. Fluid Mech. 674, 67–92.CrossRefGoogle Scholar
46. Yang, Y., Pullin, D. I. & Bermejo-Moreno, I. 2010 Multi-scale geometrical analysis of Lagrangian structures in isotropic turbulence. J. Fluid Mech. 654, 233–270.CrossRefGoogle Scholar