Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T21:57:12.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric-control formulation and averaging analysis of the unsteady aerodynamics of a wing with oscillatory controls

Published online by Cambridge University Press:  12 October 2021

Haithem E. Taha Open the ORCID record for Haithem E. Taha [Opens in a new window] ,
Laura Pla Olea Open the ORCID record for Laura Pla Olea [Opens in a new window] ,
Nabil Khalifa Open the ORCID record for Nabil Khalifa [Opens in a new window] ,
Cody Gonzalez Open the ORCID record for Cody Gonzalez [Opens in a new window]  and
Amir S. Rezaei Open the ORCID record for Amir S. Rezaei [Opens in a new window]
Haithem E. Taha*
Affiliation:
Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
Laura Pla Olea
Affiliation:
Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
Nabil Khalifa
Affiliation:
Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
Cody Gonzalez
Affiliation:
Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
Amir S. Rezaei
Affiliation:
Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Differential-geometric-control theory represents a mathematically elegant combination of differential geometry and control theory. Practically, it allows exploitation of nonlinear interactions between various inputs for the generation of forces in non-intuitive directions. Since its early developments in the 1970s, the geometric-control theory has not been duly exploited in the area of fluid mechanics. In this paper, we show the potential of geometric-control theory in the analysis of fluid flows, exemplifying it as a heuristic analysis tool for discovery of symmetry-breaking and unconventional force-generation mechanisms. In particular, we formulate the wing unsteady aerodynamics problem in a geometric-control framework. To achieve this goal, we develop a reduced-order model for the unsteady flow over a pitching–plunging wing that is (i) rich enough to capture the main physical aspects (e.g. nonlinearity of the flow dynamics at large angles of attack and high frequencies) and (ii) efficient and compact enough to be amenable to the analytic tools of geometric nonlinear control theory. We then combine tools from geometric-control theory and averaging to analyse the developed reduced-order dynamical model, which reveals regimes for lift and thrust enhancement mechanisms. The unsteady Reynolds-averaged Navier–Stokes equations are simulated to validate the theoretical findings and scrutinize the underlying physics behind these enhancement mechanisms.

JFM classification

Flow Control: Control theory Mathematical Foundations: General fluid mechanics Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 928 , 10 December 2021 , A30
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abraham, I., De La Torre, G. & Murphey, T.D. 2017 Model-based control using koopman operators. arXiv:1709.01568.CrossRefGoogle Scholar
ADCL 2019 a Stabilization of an inverted pendulum under high-frequency excitation (kapitza pendulum). https://www.youtube.com/watch?v=GgYABmG_bto, accessed: 07-11-2017.Google Scholar
ADCL 2019 b Stabilization of an inverted pendulum under high-frequency excitation (kapitza pendulum). https://www.youtube.com/watch?v=Tnv186IFovQ, accessed: 03-17-2021.Google Scholar
Agrachev, A.A. & Gamkrelidze, R.V. 1978 The exponential representation of flows and the chronological calculus. Math. Sbornik 149 (4), 467–532.Google Scholar
Alben, S. & Shelley, M. 2005 Coherent locomotion as an attracting state for a free flapping body. Proc. Natl Acad. Sci. USA 102 (32), 11163–11166.CrossRefGoogle ScholarPubMed
Andro, J.-Y. & Jacquin, L. 2009 Frequency effects on the aerodynamic mechanisms of a heaving airfoil in a forward flight configuration. Aerosp. Sci. Technol. 13 (1), 71–80.CrossRefGoogle Scholar
Ansari, S.A., Żbikowski, R. & Knowles, K. 2006 Non-linear unsteady aerodynamic model for insect-like flapping wings in the hover. Part 1: methodology and analysis. Proc. Inst. Mech. Engrs 220 (2), 61–83.CrossRefGoogle Scholar
Arnold, V.I. 1966 a On an a priori estimate in the theory of hydrodynamical stability. Izu. Vyssh. Uchebn. Zaued. Matematika 54 (5), 3–5.Google Scholar
Arnold, V.I. 1966 b Sur la géométrie différentielle des groupes de lie de dimension infinie et ses applications à l'hydrodynamique des fluides parfaits. In Annales de l'institut Fourier, vol. 16, pp. 319–361.Google Scholar
Arnold, V.I. 1969 Hamiltonian nature of the euler equations in the dynamics of a rigid body and of an ideal fluid. In Vladimir I. Arnold-Collected Works (ed. A.B. Givental, B. Khesin, A.N. Varchenko, V.A. Vassiliev & O.Y. Viro), pp. 175–178. Springer.CrossRefGoogle Scholar
Arnol'd, V.I. 2013 Mathematical Methods of Classical Mechanics, vol. 60. Springer Science & Business Media.Google Scholar
Baik, Y.S., Bernal, L.P., Granlund, K. & Ol, M.V. 2012 Unsteady force generation and vortex dynamics of pitching and plunging aerofoils. J. Fluid Mech. 709, 37–68.CrossRefGoogle Scholar
Baillieul, J. & Lehman, B. 1996 Open-loop control using oscillatory inputs. In CRC Control Handbook (ed. W.S. Levine), pp. 967–980.Google Scholar
Bloch, A.M., Holm, D.D., Crouch, P.E. & Marsden, J.E. 2000 An optimal control formulation for inviscid incompressible ideal fluid flow. In Proceedings of the 39th IEEE Conference on Decision and Control (Cat. No. 00CH37187), vol. 2, pp. 1273–1278. IEEE.Google Scholar
Borisov, A.V., Mamaev, I.S. & Ramodanov, S.M. 2003 Motion of a circular cylinder and n point vortices in a perfect fluid. Regular Chaotic Dyn. 8 (4), 449–462.CrossRefGoogle Scholar
Borisov, A.V., Mamaev, I.S. & Ramodanov, S.M. 2007 Dynamic interaction of point vortices and a two-dimensional cylinder. J. Maths Phys. 48 (6), 065403.CrossRefGoogle Scholar
Brockett, R.W. 1972 System theory on group manifolds and coset spaces. SIAM J. Control 10 (2), 265–284.CrossRefGoogle Scholar
Brockett, R.W. 1976 Nonlinear systems and differential geometry. Proc. IEEE 64 (1), 61–72.CrossRefGoogle Scholar
Brockett, R.W. 1978 Feedback invariants for nonlinear systems. IFAC Proc. Volumes 11 (1), 1115–1120.CrossRefGoogle Scholar
Brockett, R.W. 1982 Control theory and singular Riemannian geometry. In New Directions in Applied Mathematics (ed. P.J. Hilton & G.S. Young), pp. 11–27. Springer.CrossRefGoogle Scholar
Brockett, R.W. 1983 Asymptotic stability and feedback stabilization. In Differential Geometric Control Theory 27.1, pp. 181–191.Google Scholar
Brunton, S.L., Brunton, B.W., Proctor, J.L. & Kutz, J.N. 2016 a Koopman invariant subspaces and finite linear representations of nonlinear dynamical systems for control. PLoS One 11 (2), e0150171.CrossRefGoogle ScholarPubMed
Brunton, S.L., Proctor, J.L. & Kutz, J.N. 2016 b Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113 (15), 3932–3937.CrossRefGoogle ScholarPubMed
Bullo, F. 2002 Averaging and vibrational control of mechanical systems. SIAM J. Control Optim. 41 (2), 542–562.CrossRefGoogle Scholar
Bullo, F. & Lewis, A.D. 2004 Geometric Control of Mechanical Systems. Springer.Google Scholar
Buzhardt, J., Fedonyuk, V. & Tallapragada, P. 2018 Pairwise controllability and motion primitives for micro-rotors in a bounded stokes flow. Intl J. Intell. Robot. Appl. 2 (4), 454–461.CrossRefGoogle Scholar
Carr, L.W. 1988 Progress in analysis and prediction of dynamic stall. J. Aircraft 25 (1), 6–17.CrossRefGoogle Scholar
Chiereghin, N., Cleaver, D.J. & Gursul, I. 2019 Unsteady lift and moment of a periodically plunging airfoil. AIAA J. 57 (1), 208–222.CrossRefGoogle Scholar
Choi, J., Colonius, T. & Williams, D.R. 2015 Surging and plunging oscillations of an airfoil at low Reynolds number. J. Fluid Mech. 763, 237–253.CrossRefGoogle Scholar
Cleaver, D.J., Wang, Z. & Gursul, I. 2012 Bifurcating flows of plunging aerofoils at high Strouhal numbers. J. Fluid Mech. 708, 349–376.CrossRefGoogle Scholar
Cleaver, D.J., Wang, Z. & Gursul, I. 2013 Investigation of high-lift mechanisms for a flat-plate airfoil undergoing small-amplitude plunging oscillations. AIAA J. 51 (4), 968–980.CrossRefGoogle Scholar
Cleaver, D.J., Wang, Z., Gursul, I. & Visbal, M.R. 2011 Lift enhancement by means of small-amplitude airfoil oscillations at low Reynolds numbers. AIAA J. 49 (9), 2018–2033.CrossRefGoogle Scholar
Crouch, P.E. 1984 Spacecraft attitude control and stabilization: applications of geometric control theory to rigid body models. IEEE Trans. Autom. Control 29 (4), 321–331.CrossRefGoogle Scholar
Dickinson, M.H., Lehmann, F.-O. & Sane, S.P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284 (5422), 1954–1960.CrossRefGoogle ScholarPubMed
Dickson, W.B. & Dickinson, M.H. 2004 The effect of advance ratio on the aerodynamics of revolving wings. J. Expl Biol. 207, 4269–4281.CrossRefGoogle ScholarPubMed
Dritschel, D.G. & Boatto, S. 2015 The motion of point vortices on closed surfaces. Proc. R. Soc. Lond. A 471 (2176), 20140890.Google Scholar
Dugas, R. 1988 A History of Mechanics, Translated into English by JR Maddox. Dover.Google Scholar
Ekaterinaris, J.A. & Platzer, M.F. 1998 Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 33 (11–12), 759–846.CrossRefGoogle Scholar
Ellington, C.P., Van Den Berg, C., Willmott, A.P. & Thomas, A.L.R. 1996 Leading-edge vortices in insect flight. Nature 384, 626–630.CrossRefGoogle Scholar
Fairchild, M.J., Hassing, P.M., Kelly, S.D., Pujari, P. & Tallapragada, P. 2011 Single-input planar navigation via proportional heading control exploiting nonholonomic mechanics or vortex shedding. In ASME 2011 Dynamic Systems and Control Conference and Bath/ASME Symposium on Fluid Power and Motion Control, pp. 345–352. American Society of Mechanical Engineers Digital Collection.CrossRefGoogle Scholar
Fenercioglu, I. & Cetiner, O. 2014 Effect of unequal flapping frequencies on flow structures. Aerosp. Sci. Technol. 35, 39–53.CrossRefGoogle Scholar
Fliess, M., Lamnabhi, M. & Lamnabhi-Lagarrigue, F. 1983 An algebraic approach to nonlinear functional expansions. IEEE Trans. Circuits Syst. 30 (8), 554–570.CrossRefGoogle Scholar
Garrick, I.E. 1937 Propulsion of a flapping and oscillating airfoil. NACA Tech. Rep. NACA-TR-567. National Advisory Committee for Aeronautics.Google Scholar
Garrick, I.E. 1938 On some reciprocal relations in the theory of nonstationary flows. NACA Tech. Rep. 629. National Advisory Committee for Aeronautics.Google Scholar
Goman, M. & Khrabrov, A. 1994 State-space representation of aerodynamic characteristics of an aircraft at high angles of attack. J. Aircraft 31 (5), 1109–1115.CrossRefGoogle Scholar
Gupta, R. & Ansell, P.J. 2019 Unsteady flow physics of airfoil dynamic stall. AIAA J. 57 (1), 165–175.CrossRefGoogle Scholar
Gursul, I., Cleaver, D.J. & Wang, Z. 2014 Control of low Reynolds number flows by means of fluid–structure interactions. Prog. Aerosp. Sci. 64, 17–55.CrossRefGoogle Scholar
Hassan, A.M. & Taha, H.E. 2017 Geometric control formulation and nonlinear controllability of airplane flight dynamics. Nonlinear Dyn. 88 (4), 2651–2669.CrossRefGoogle Scholar
Hassan, A.M. & Taha, H.E. 2019 Differential-geometric-control formulation of flapping flight multi-body dynamics. J. Nonlinear Sci. 29, 1379–1417.CrossRefGoogle Scholar
Hassan, A.M. & Taha, H.E. 2021 Design of a nonlinear roll mechanism for airplanes using lie brackets for high alpha operation. IEEE Trans. Aerosp. Electron. Syst. 57 (1), 462–475.CrossRefGoogle Scholar
Hemati, M.S., Eldredge, J.D. & Speyer, J.L. 2014 Improving vortex models via optimal control theory. J. Fluids Struct. 49, 91–111.CrossRefGoogle Scholar
Hermann, R. 1962 The differential geometry of foliations. II. J. Math. Mech. 11, 303–315.Google Scholar
Hermann, R. 1963 On the accessibility problem in control theory. In International Symposium on Nonlinear Differential Equations and Nonlinear Mechanics, pp. 325–332. Elsevier.CrossRefGoogle Scholar
Holm, D.D., Marsden, J.E. & Ratiu, T.S. 1998 The Euler–Poincaré equations and semidirect products with applications to continuum theories. Adv. Math. 137 (1), 1–81.CrossRefGoogle Scholar
Huang, B. & Vaidya, U. 2018 Data-driven approximation of transfer operators: naturally structured dynamic mode decomposition. In 2018 Annual American Control Conference (ACC), pp. 5659–5664. IEEE.CrossRefGoogle Scholar
Hussein, A.A., Taha, H., Ragab, S. & Hajj, M.R. 2018 A variational approach for the dynamics of unsteady point vortices. Aerosp. Sci. Technol. 78, 559–568.CrossRefGoogle Scholar
Isidori, A. 1995 Nonlinear Control Systems, vol. 1. Springer Science & Business Media.CrossRefGoogle Scholar
Jakubczyk, B. & Respondek, W. 1980 On linearization of control systems. Bull. Acad. Pol. Sci. Ser. Sci. Math. 28 (9–10), 517–522.Google Scholar
Jones, M.A. 2003 The separated flow of an inviscid fluid around a moving flat plate. J. Fluid Mech. 496, 405–441.CrossRefGoogle Scholar
Jones, R.T. 1938 Operational treatment of the nonuniform lift theory to airplane dynamics. NACA Tech. Rep. 667. National Advisory Committee for Aeronautics.Google Scholar
Jones, W.P. 1945 Aerodynamic forces on wings in non-uniform motion. Tech. Rep. 2117. British Aeronautical Research Council.Google Scholar
Juang, J.-N. & Pappa, R.S. 1985 An eigensystem realization algorithm for modal parameter identification and model reduction. J. Guid. Control Dyn. 8 (5), 620–627.CrossRefGoogle Scholar
Kambe, T. 2009 Geometrical Theory of Dynamical Systems and Fluid Flows, vol. 23. World Scientific.CrossRefGoogle Scholar
Kanso, E., Marsden, J.E., Rowley, C.W. & Melli-Huber, J.B. 2005 Locomotion of articulated bodies in a perfect fluid. J. Nonlinear Sci. 15 (4), 255–289.CrossRefGoogle Scholar
Karniadakis, G.E. & Triantafyllou, G.S. 1989 Frequency selection and asymptotic states in laminar wakes. J. Fluid Mech. 199, 441–469.CrossRefGoogle Scholar
Kelly, S.D. & Hukkeri, R.B. 2006 Mechanics, dynamics, and control of a single-input aquatic vehicle with variable coefficient of lift. IEEE Trans. Robot. 22 (6), 1254–1264.CrossRefGoogle Scholar
Kelly, S.D. & Murray, R.M. 2000 Modelling efficient pisciform swimming for control. Intl J. Robust Nonlinear Control 10 (4), 217–241.3.0.CO;2-X>CrossRefGoogle Scholar
Kelly, S.D., Pujari, P. & Xiong, H. 2012 Geometric mechanics, dynamics, and control of fishlike swimming in a planar ideal fluid. In Natural Locomotion in Fluids and on Surfaces, pp. 101–116. Springer.CrossRefGoogle Scholar
Kelly, S.D. & Xiong, H. 2010 Self-propulsion of a free hydrofoil with localized discrete vortex shedding: analytical modeling and simulation. Theor. Comput. Fluid Dyn. 24 (1–4), 45–50.CrossRefGoogle Scholar
Khalil, H.K. 2002 Noninear Systems. Prentice-Hall.Google Scholar
Küssner, H.G. 1929 Schwingungen von flugzeugflügeln. In Jahrbuch der deutscher Versuchsanstalt für Luftfahrt especially Section E3 Einfluss der Baustoff-Dämpfung, pp. 319–320.Google Scholar
Kwatny, H.G., Dongmo, J.-E.T., Chang, B.-C., Bajpai, G., Yasar, M. & Belcastro, C. 2012 Nonlinear analysis of aircraft loss of control. J. Guid. Control Dyn. 36 (1), 149–162.CrossRefGoogle Scholar
Lee, T. & Gerontakos, P. 2004 Investigation of flow over an oscillating airfoil. J. Fluid Mech. 512, 313–341.CrossRefGoogle Scholar
Leishman, J.G. & Beddoes, T.S. 1989 A semi-empirical model for dynamic stall. J. Am. Helicopter Soc. 34 (3), 3–17.Google Scholar
Leishman, J.G. & Crouse, G.L. 1989 State-Space Model for Unsteady Airfoil Behavior and Dynamic Stall, pp. 1372–1383. AIAA.Google Scholar
Leishman, J.G. & Nguyen, K.Q. 1990 State-space representation of unsteady airfoil behavior. AIAA J. 28 (5), 836–844.CrossRefGoogle Scholar
Leonard, N.E. & Krishnaprasad, P.S. 1995 Motion control of drift-free, left-invariant systems on Lie groups. IEEE Trans. Autom. Control 40 (9), 1539–1554.CrossRefGoogle Scholar
Lesieur, M., Métais, O. & Comte, P. 2005 Large-Eddy Simulations of Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Li, J. & Wu, Z.-N. 2015 Unsteady lift for the wagner problem in the presence of additional leading/trailing edge vortices. J. Fluid Mech. 769, 182–217.CrossRefGoogle Scholar
Lieu, B.K., Moarref, R. & Jovanović, M.R. 2010 Controlling the onset of turbulence by streamwise travelling waves. Part 2. Direct numerical simulation. J. Fluid Mech. 663, 100–119.CrossRefGoogle Scholar
Lighthill, J. 1975 Aerodynamic aspects of animal flight. In Swimming and Flying in Nature, pp. 423–491. Springer.CrossRefGoogle Scholar
Liu, W. 1997 a An approximation algorithm for nonholonomic systems. SIAM J. Control Optim. 35 (4), 1328–1365.CrossRefGoogle Scholar
Liu, W. 1997 b Averaging theorems for highly oscillatory differential equations and iterated Lie brackets. SIAM J. Control Optim. 35 (6), 1989–2020.CrossRefGoogle Scholar
Loewy, R.G. 1957 A two-dimensional approximation to unsteady aerodynamics in rotary wings. J. Aeronaut. Sci. 24, 81–92.CrossRefGoogle Scholar
Lumley, J.L. 2007 Stochastic Tools in Turbulence. Courier Corporation.Google Scholar
Maggia, M., Eisa, S. & Taha, H. 2019 On higher-order averaging of time-periodic systems: reconciliation of two averaging techniques. Nonlinear Dyn. 99, 813–836.CrossRefGoogle Scholar
Marsden, J. & Weinstein, A. 1983 Coadjoint orbits, vortices, and clebsch variables for incompressible fluids. Physica D 7 (1), 305–323.CrossRefGoogle Scholar
Marsden, J.E. 1997 Geometric foundations of motion and control. In Motion, Control, and Geometry: Proceedings of a Symposium, Board on Mathematical Science, National Research Council Education, Washington DC, pp. 3–19. National Academies Press.Google Scholar
Marsden, J.E., O'Reilly, O.M., Wicklin, F.J. & Zombros, B.W. 1991 Symmetry, stability, geometric phases, and mechanical integrators. Nonlinear Sci. Today 1 (1), 4–11.Google Scholar
McCroskey, W.J., McAlister, K.W., Carr, L.W. & Pucci, S.L. 1982 An experimental study of dynamic stall on advanced airfoil section. Volume 1: summary of the experiment. NACA Tech. Mem. 84245.Google Scholar
Meerkov, S.M. 1980 Principle of vibrational control: theory and applications. IEEE Trans. Autom. Control 25 (4), 755–762.CrossRefGoogle Scholar
Menter, F.R. 1994 Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32 (8), 1598–1605.Google Scholar
Minotti, F.O. 2002 Unsteady two-dimensional theory of a flapping wing. Phys. Rev. E 66 (5), 051907.CrossRefGoogle ScholarPubMed
Mir, I., Taha, H., Eisa, S. & Maqsood, A. 2018 A Controllability Perspective of Dynamic Soaring, vol. 94, pp. 2347–2362. Springer.Google Scholar
Moarref, R. & Jovanović, M.R. 2010 Controlling the onset of turbulence by streamwise travelling waves. Part 1. Receptivity analysis. J. Fluid Mech. 663, 70–99.CrossRefGoogle Scholar
Moarref, R. & Jovanović, M.R. 2012 Model-based design of transverse wall oscillations for turbulent drag reduction. J. Fluid Mech. 707, 205–240.CrossRefGoogle Scholar
Morgansen, K.A., Duidam, V., Mason, R.J., Burdick, J.W. & Murray, R.M. 2001 Nonlinear control methods for planar carangiform robot fish locomotion. In Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation, 2001, vol. 1, pp. 427–434. IEEE.Google Scholar
Morgansen, K.A., Vela, P.A. & Burdick, J.W. 2002 Trajectory stabilization for a planar carangiform robot fish. In Proceedings ICRA’02. IEEE International Conference on Robotics and Automation, 2002, vol. 1, pp. 756–762. IEEE.Google Scholar
Murray, R.M., Li, Z. & Sastry, S.S. 1994 A Mathematical Introduction to Robotic Manipulation. CRC.Google Scholar
Murray, R.M. & Sastry, S.S. 1993 Nonholonomic motion planning: steering using sinusoids. IEEE Trans. Autom. Control 38 (5), 700–716.CrossRefGoogle Scholar
Narsipur, S., Hosangadi, P., Gopalarathnam, A. & Edwards, J.R. 2016 Variation of leading-edge suction at stall for steady and unsteady airfoil motions. In 54th AIAA Aerospace Sciences Meeting, p. 1354.Google Scholar
Nayfeh, A.H. 1973 Perturbation Methods. John Wiley and Sons, Inc.Google Scholar
Nayfeh, A.H. & Balachandran, B. 2004 Applied Nonlinear Dynamics. WILEY-VCH Verlag GmbH & Co. KGaA.Google Scholar
Nayfeh, A.H. & Mook, D.T. 1979 Nonlinear Oscillations. John Wiley and Sons, Inc.Google Scholar
Nijmeijer, H. & Van der Schaft, A. 1990 Nonlinear Dynamical Control Systems. Springer.CrossRefGoogle Scholar
Ogata, K. & Yang, Y. 1970 Modern control engineering. Prentice Hall.Google Scholar
Panah, A.E. & Buchholz, J.H.J. 2014 Parameter dependence of vortex interactions on a two-dimensional plunging plate. Exp. Fluids 55 (3), 1687.CrossRefGoogle Scholar
Peters, D.A. 2008 Two-dimensional incompressible unsteady airfoil theory—an overview. J. Fluids Struct. 24, 295–312.CrossRefGoogle Scholar
Peters, D.A., Karunamoorthy, S. & Cao, W. 1995 Finite-state induced flow models, Part I: two-dimensional thin airfoil. J. Aircraft 44, 1–28.Google Scholar
Pla Olea, L. 2019 Geometric control theoretic formulation applied to the analysis of pitching and plunging airfoils. Master's thesis, UC Irvine.Google Scholar
Polhamus, E.C. 1966 A concept of the vortex lift of sharp-edge delta wings based on a leading-edge-suction analogy. NASA Tech. Rep. NASA TN D-3767.Google Scholar
Pollard, B., Fedonyuk, V. & Tallapragada, P. 2019 Swimming on limit cycles with nonholonomic constraints. Nonlinear. Dyn. 97 (4), 2453–2468.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pullin, D.I. & Wang, Z. 2004 Unsteady forces on an accelerating plate and application to hovering insect flight. J. Fluid Mech. 509, 1–21.CrossRefGoogle Scholar
Ramesh, K. 2020 On the leading-edge suction and stagnation-point location in unsteady flows past thin aerofoils. J. Fluid Mech. 886, A13.CrossRefGoogle Scholar
Ramesh, K., Gopalarathnam, A., Granlund, K., Ol, M.V. & Edwards, J.R. 2014 Discrete-vortex method with novel shedding criterion for unsteady aerofoil flows with intermittent leading-edge vortex shedding. J. Fluid Mech. 751, 500–538.Google Scholar
Raveh, D.E. 2001 Reduced-order models for nonlinear unsteady aerodynamics. AIAA J. 39 (8), 1417–1429.CrossRefGoogle Scholar
Rival, D. & Tropea, C. 2010 Characteristics of pitching and plunging airfoils under dynamic-stall conditions. J. Aircraft 47 (1), 80–86.CrossRefGoogle Scholar
Rival, D.E., Kriegseis, J., Schaub, P., Widmann, A. & Tropea, C. 2014 Characteristic length scales for vortex detachment on plunging profiles with varying leading-edge geometry. Exp. Fluids 55 (1), 1660.CrossRefGoogle Scholar
Rowley, C.W. 2005 Model reduction for fluids, using balanced proper orthogonal decomposition. Intl J. Bifurcation Chaos 15 (03), 997–1013.CrossRefGoogle Scholar
Rowley, C.W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D.S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
Rozhdestvensky, K.V. & Ryzhov, V.A. 2003 Aerohydrodynamics of flapping-wing propulsors. Prog. Aerosp. Sci. 39 (8), 585–633.CrossRefGoogle Scholar
Sanders, J.A., Verhulst, F. & Murdock, J.A. 2007 Averaging Methods in Nonlinear Dynamical Systems, vol. 2. Springer.Google Scholar
Sarychev, A. 2001 Stability criteria for time-periodic systems via high-order averaging techniques. In Nonlinear Control in the Year 2000 (ed. Alberto Isidori et al.), Lecture Notes in Control and Information Sciences, vol. 2, pp. 365–377. Springer.CrossRefGoogle Scholar
Sassano, M. & Astolfi, A. 2016 Approximate dynamic tracking and feedback linearization. In 2016 IEEE 55th Conference on Decision and Control (CDC), pp. 5688–5693. IEEE.CrossRefGoogle Scholar
Sastry, S. 1999 Nonlinear Systems: Analysis, Stability, and Control, vol. 10. Springer.CrossRefGoogle Scholar
Schlichting, H., Gersten, K., Krause, E., Oertel, H. & Mayes, K. 1960 Boundary-Layer Theory, vol. 7. Springer.Google Scholar
Schlichting, H. & Truckenbrodt, E. 1979 Aerodynamics of the Airplane. McGraw-Hill.Google Scholar
Schmid, P.J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Schwarz, L. 1940 Brechnung der druckverteilung einer harmonisch sich verformenden tragflache in ebener stromung, vol. 17. Luftfahrtforsch.Google Scholar
Sears, W.R. 1956 Some recent developments in airfoil theory. J. Aeronaut. Sci. 23 (5), 490–499.CrossRefGoogle Scholar
Sears, W.R. 1941 Some aspects of non-stationary airfoil theory and its practical application. J. Aeronaut. Sci. 8 (3), 104–108.CrossRefGoogle Scholar
Sedov, L.I. 1980 Two-dimensional problems of hydrodynamics and aerodynamics. Moscow Izdatel Nauka 1.Google Scholar
Shashikanth, B.N. 2005 Poisson brackets for the dynamically interacting system of a 2d rigid cylinder and n point vortices: the case of arbitrary smooth cylinder shapes. Regular Chaotic Dyn. 10 (1), 1–14.Google Scholar
Shashikanth, B.N., Marsden, J.E., Burdick, J.W. & Kelly, S.D. 2002 The hamiltonian structure of a two-dimensional rigid circular cylinder interacting dynamically with $n$ point vortices. Phys. Fluids (1994-present) 14 (3), 1214–1227.CrossRefGoogle Scholar
Shashikanth, B.N., Sheshmani, A., Kelly, S.D. & Marsden, J.E. 2008 Hamiltonian structure for a neutrally buoyant rigid body interacting with n vortex rings of arbitrary shape: the case of arbitrary smooth body shape. Theor. Comput. Fluid Dyn. 22 (1), 37–64.CrossRefGoogle Scholar
Shashikanth, B.N., Sheshmani, A., Kelly, S.D. & Wei, M. 2010 Hamiltonian structure and dynamics of a neutrally buoyant rigid sphere interacting with thin vortex rings. J. Math. Fluid Mech. 12 (3), 335–353.Google Scholar
Silva, W.A. 1993 Application of nonlinear systems theory to transonic unsteady aerodynamic responses. J. Aircraft 30 (5), 660–668.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Maths 45 (3), 561–571.CrossRefGoogle Scholar
Sussmann, H.J. 1973 Orbits of families of vector fields and integrability of distributions. Trans. Am. Math. Soc. 180, 171–188.CrossRefGoogle Scholar
Sussmann, H.J. 1987 A general theorem on local controllability. SIAM J. Control Optim. 25 (1), 158–194.Google Scholar
Sussmann, H.J. & Jurdjevic, V. 1972 Controllability of nonlinear systems. J. Differ. Equ. 12 (1), 95–116.Google Scholar
Taha, H. 2018 Can flapping propulsion boost airplane technology? The flapping-tail concept airplane. AIAA Paper 2018-0547.CrossRefGoogle Scholar
Taha, H., Hajj, M.R. & Beran, P.S. 2014 State space representation of the unsteady aerodynamics of flapping flight. Aerosp. Sci. Technol. 34, 1–11.CrossRefGoogle Scholar
Taha, H., Kiani, M., Hedrick, T.L. & Greeter, J.S.M. 2020 Vibrational control: a hidden stabilization mechanism in insect flight. Sci. Robot. 5 (46), eabb1502.CrossRefGoogle ScholarPubMed
Taha, H. & Rezaei, A.S. 2020 On the high-frequency response of unsteady lift and circulation: a dynamical systems perspective. J. Fluids Struct. 93, 102868.CrossRefGoogle Scholar
Taha, H., Tahmasian, S., Woolsey, C.A., Nayfeh, A.H. & Hajj, M.R. 2015 a The need for higher-order averaging in the stability analysis of hovering mavs/insects. Bioinspir. Biomim. 10 (1), 016002.CrossRefGoogle Scholar
Taha, H., Woolsey, C.A. & Hajj, M.R. 2015 b Geometric control approach to longitudinal stability of flapping flight. J. Guid. Control Dyn. 39 (2), 214–226.CrossRefGoogle Scholar
Taha, H.E. & Hassan, A.M. 2021 Nonlinear flight physics of the Lie-bracket roll mechanism. AIAA Paper 2021-0252.CrossRefGoogle Scholar
Tahmasian, S. & Woolsey, C.A. 2017 Flight control of biomimetic air vehicles using vibrational control and averaging. J. Nonlinear Sci. 27 (4), 1193–1214.CrossRefGoogle Scholar
Tallapragada, P. & Kelly, S.D. 2013 Reduced-order modeling of propulsive vortex shedding from a free pitching hydrofoil with an internal rotor. In American Control Conference (ACC), 2013, pp. 615–620. IEEE.CrossRefGoogle Scholar
Tallapragada, P. & Kelly, S.D. 2017 Integrability of velocity constraints modeling vortex shedding in ideal fluids. J. Comput. Nonlinear Dyn. 12 (2), 021008.Google Scholar
Theodorsen, T. 1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. 496. National Advisory Committee for Aeronautics.Google Scholar
Usherwood, J.R. & Ellington, C.P. 2002 The aerodynamics of revolving wings. I. Model hawkmoth wings. J. Expl Biol. 205, 1547–1564.CrossRefGoogle ScholarPubMed
Vandenberghe, N., Zhang, J. & Childress, S. 2004 Symmetry breaking leads to forward flapping flight. J. Fluid Mech. 506, 147–155.CrossRefGoogle Scholar
Vela, P.A. 2003 Averaging and control of nonlinear systems (with application to biomimetic locomotion). PhD thesis, California Institute of Technology.Google Scholar
Vela, P.A., Morgansen, K.A. & Burdick, J.W. 2002 Underwater locomotion from oscillatory shape deformations. In Proceedings of the IEEE Conference on Decision and Control, Las Vegas, NV, vol. 2, pp. 2074–2080.Google Scholar
Vepa, R. 1976 On the use of pade approximants to represent unsteady aerodynamic loads for arbitrarily small motions of wings. AIAA Paper 1976-17.CrossRefGoogle Scholar
Von Kármán, T. & Sears, W.R. 1938 Airfoil theory for non-uniform motion. J. Aeronaut. Sci. 5 (10), 379–390.CrossRefGoogle Scholar
Wagner, H. 1925 Uber die entstehung des dynamischen auftriebs von tragflugeln. Z. Angew. Math. Mech. 5, 17–35.CrossRefGoogle Scholar
Walsh, G.C. & Sastry, S.S. 1995 On reorienting linked rigid bodies using internal motions. IEEE Trans. Robot. Automat. 11 (1), 139–146.CrossRefGoogle Scholar
Wang, C. & Eldredge, J.D. 2013 Low-order phenomenological modeling of leading-edge vortex formation. Theor. Comput. Fluid Dyn. 27 (5), 577–598.CrossRefGoogle Scholar
Wang, Z.J., Birch, J.M. & Dickinson, M.H. 2004 Unsteady forces in hovering flight: computation vs experiments. J. Expl Biol. 207, 449–460.CrossRefGoogle Scholar
Webb, C., Dong, H. & Ol, M. 2008 Effects of unequal pitch and plunge airfoil motion frequency on aerodynamic response. AIAA Paper 2021-1830.CrossRefGoogle Scholar
Wilcox, D.C. 2008 Formulation of the kw turbulence model revisited. AIAA J. 46 (11), 2823–2838.CrossRefGoogle Scholar
Wilcox, D.C. 1998 Turbulence Modeling for CFD, vol. 2. DCW industries La Canada.Google Scholar
Williams, M.O., Kevrekidis, I.G. & Rowley, C.W. 2015 A data–driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25 (6), 1307–1346.CrossRefGoogle Scholar
Woolsey, C.A. & Leonard, N.E. 2002 Stabilizing underwater vehicle motion using internal rotors. Automatica 38 (12), 2053–2062.CrossRefGoogle Scholar
Xiao, Q. & Liao, W. 2010 Computational study of oscillating hydrofoil with different plunging/pitching frequency. J. Aero Aqua Biomech. 1 (1), 64–70.CrossRefGoogle Scholar
Yan, Z., Taha, H. & Hajj, M.R. 2014 Geometrically-exact unsteady model for airfoils undergoing large amplitude maneuvers. Aerosp. Sci. Technol. 39, 293–306.CrossRefGoogle Scholar
Yongliang, Y., Binggang, T. & Huiyang, M. 2003 An analytic approach to theoretical modeling of highly unsteady viscous flow excited by wing flapping in small insects. Acta Mechanica Sin. 19 (6), 508–516.CrossRefGoogle Scholar
Young, J. & Lai, J.C. 2007 Vortex lock-in phenomenon in the wake of a plunging airfoil. AIAA J. 45 (2), 485–490.CrossRefGoogle Scholar

Taha et al. Supplementary Movie 1

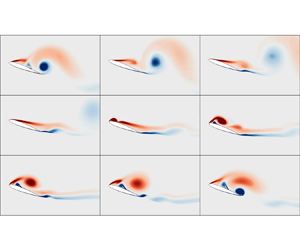
Vorticity contours over the plunging cycle around mean angle of attack of 15◦, with reduced frequency k = 0.5 and plunging amplitude of 5◦ effective angle of attack. This low-amplitude, high-frequency plunging around the stall point (negative curvature of the steady lift curve) of NACA 0012 does not trigger a considerable leading edge vortex. A decrease in the mean lift coefficient is observed.

Download Taha et al. Supplementary Movie 1(Video)
Video 344.7 KB

Taha et al. Supplementary Movie 2

Vorticity contours over the plunging cycle around mean angle of attack of 20◦, with reduced frequency k = 0.5 and plunging amplitude of 5◦ effective angle of attack. This low-amplitude, high-frequency plunging in the post-stall regime (positive curvature of the steady lift curve) of NACA 0012 triggers a considerable leading edge vortex, which leads to enhancement in the mean lift coefficient beyond the steady value.

Download Taha et al. Supplementary Movie 2(Video)
Video 595.2 KB