Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-17T13:21:05.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometrical shock dynamics for magnetohydrodynamic fast shocks

Published online by Cambridge University Press:  12 December 2016

W. Mostert ,
D. I. Pullin ,
R. Samtaney  and
V. Wheatley
W. Mostert*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, CA 91125, USA
D. I. Pullin
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, CA 91125, USA
R. Samtaney
Affiliation:
Mechanical Engineering, Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
V. Wheatley
Affiliation:
School of Mechanical and Mining Engineering, University of Queensland, QLD 4072, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe a formulation of two-dimensional geometrical shock dynamics (GSD) suitable for ideal magnetohydrodynamic (MHD) fast shocks under magnetic fields of general strength and orientation. The resulting area–Mach-number–shock-angle relation is then incorporated into a numerical method using pseudospectral differentiation. The MHD-GSD model is verified by comparison with results from nonlinear finite-volume solution of the complete ideal MHD equations applied to a shock implosion flow in the presence of an oblique and spatially varying magnetic field ahead of the shock. Results from application of the MHD-GSD equations to the stability of fast MHD shocks in two dimensions are presented. It is shown that the time to formation of triple points for both perturbed MHD and gas-dynamic shocks increases as 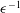$\unicode[STIX]{x1D716}^{-1}$, where $\unicode[STIX]{x1D716}$ is a measure of the initial Mach-number perturbation. Symmetry breaking in the MHD case is demonstrated. In cylindrical converging geometry, in the presence of an azimuthal field produced by a line current, the MHD shock behaves in the mean as in Pullin et al. (Phys. Fluids, vol. 26, 2014, 097103), but suffers a greater relative pressure fluctuation along the shock than the gas-dynamic shock.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Shock waves MHD and Electrohydrodynamics: MHD and Electrohydrodynamics
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 811 , 25 January 2017 , R2
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34 (1), 445–468.CrossRefGoogle Scholar
Cao, J., Wu, Z., Ren, H. & Li, D. 2008 Effects of shear flow and transverse magnetic field on Richtmyer–Meshkov instability. Phys. Plasmas 15, 042102.Google Scholar
Chisnell, R. F. 1957 The motion of a shock wave in a channel, with applications to cylindrical and spherical shock waves. J. Fluid Mech. 2, 286–298.Google Scholar
Don, W. S. 1994 Numerical study of pseudospectral method in shock wave applications. J. Comput. Phys. 110, 103–111.Google Scholar
Gelb, A. & Tadmor, E. 2000 Detection of edges in spectral data II: nonlinear enhancement. SIAM J. Numer. Anal. 38 (4), 1389–1408.Google Scholar
Gelb, A. & Tadmor, E. 2006 Adaptive edge detectors for piecewise smooth data based on the minmod limiter. J. Sci. Comput. 28 (2/3), 279–306.Google Scholar
Goedbloed, J. P., Keppens, R. & Poedts, S. 2010 Advanced Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Henshaw, W. D., Smyth, N. F. & Schwendeman, D. W. 1986 Numerical shock propagation using geometrical shock dynamics. J. Fluid Mech. 171, 519–545.CrossRefGoogle Scholar
Hou, T. Y. & Li, R. 2007 Computing nearly singular solutions using pseudo-spectral methods. J. Comput. Phys. 226, 379–397.Google Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. & Team, NIC 2014 Review of the National Ignition Campaign 2009–2012. Phys. Plasmas 21, 020501.CrossRefGoogle Scholar
Mostert, W., Pullin, D. I., Samtaney, R. & Wheatley, V. 2016 Converging cylindrical magnetohydrodynamic shock collapse onto a power-law-varying line current. J. Fluid Mech. 793, 414–443.CrossRefGoogle Scholar
Mostert, W., Wheatley, V., Samtaney, R. & Pullin, D. I. 2015 Effects of magnetic fields on magnetohydrodynamic cylindrical and spherical Richtmyer–Meshkov instability. Phys. Fluids 27, 104102.Google Scholar
Pullin, D. I., Mostert, W., Wheatley, V. & Samtaney, R. 2014 Converging cylindrical shocks in ideal magnetohydrodynamics. Phys. Fluids 26, 097103.CrossRefGoogle Scholar
Samtaney, R. 2003 Suppression of the Richtmyer–Meshkov instability in the presence of a magnetic field. Phys. Fluids 15 (8), L53–L56.CrossRefGoogle Scholar
Samtaney, R., Colella, P., Ligocki, T. J., Martin, D. F. & Jardin, S. C. 2005 An adaptive mesh semi-implicit conservative unsplit method for resistive MHD. J. Phys.: Conf. Ser. 16 (1), 40–48.Google Scholar
Schwendeman, D. 1988 Numerical shock propagation in non-uniform media. J. Fluid Mech. 188, 383–410.Google Scholar
Schwendeman, D. W. 1993 A new numerical method for shock wave propagation based on geometrical shock dynamics. Proc. R. Soc. Lond. A 441 (1912), 331–341.Google Scholar
Trakhinin, Y. 2003 A complete 2D stability analysis of fast MHD shocks in an ideal gas. Commun. Math. Phys. 236, 65–92.Google Scholar
Wheatley, V., Pullin, D. I. & Samtaney, R. 2005a Regular shock refraction at an oblique planar density interface in magnetohydrodynamics. J. Fluid Mech. 522, 179–214.Google Scholar
Wheatley, V., Pullin, D. I. & Samtaney, R. 2005b Stability of an impulsively accelerated density interface in magnetohydrodynamics. Phys. Rev. Lett. 95, 125002.CrossRefGoogle ScholarPubMed
Wheatley, V., Samtaney, R., Pullin, D. I. & Gehre, R. M. 2014 The transverse field Richtmyer–Meshkov instability in magnetohydrodynamics. Phys. Fluids 26, 016102.Google Scholar
Whitham, G. B. 1957 A new approach to problems of shock dynamics. Part I. Two-dimensional problems. J. Fluid Mech. 2, 145–171.Google Scholar
Whitham, G. B. 2011 Linear and Nonlinear Waves. Wiley.Google Scholar