Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T22:05:09.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Generation of first Mack modes in supersonic boundary layers by slow acoustic waves interacting with streamwise isolated wall roughness

Published online by Cambridge University Press:  06 February 2020

Yinhui Liu Open the ORCID record for Yinhui Liu [Opens in a new window] ,
Ming Dong Open the ORCID record for Ming Dong [Opens in a new window]  and
Xuesong Wu Open the ORCID record for Xuesong Wu [Opens in a new window]
Yinhui Liu
Affiliation:
Laboratory of High-speed Aerodynamics, Tianjin University, Tianjin 300072, PR China
Ming Dong
Affiliation:
Laboratory of High-speed Aerodynamics, Tianjin University, Tianjin 300072, PR China
Xuesong Wu*
Affiliation:
Laboratory of High-speed Aerodynamics, Tianjin University, Tianjin 300072, PR China Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates the receptivity of a supersonic boundary layer to slow acoustic waves whose characteristic frequency and wavelength are on the triple-deck scales, and the phase speed is thus asymptotically small. Acoustic waves on these scales are of special importance as they have the interesting property that a perturbation with a magnitude of $O(\unicode[STIX]{x1D716}_{u})$ in the free stream generates much larger, $O(\unicode[STIX]{x1D700}_{u}R^{1/8})$, velocity fluctuations inside the boundary layer, where $R$ is the Reynolds number based on the distance to the leading edge. Their interaction with streamwise localized roughness elements, leading to stronger receptivity, is studied using triple-deck theory and direct numerical simulations (DNS). The receptivity coefficient, defined as the ratio of the streamwise-velocity amplitude of the instability mode excited to that of the incident free-stream acoustic wave, serves to characterize receptivity efficiency. Its dependence on the roughness width, the Reynolds number $R$, the free-stream Mach number $M$ and the incident angle of the acoustic wave is examined. 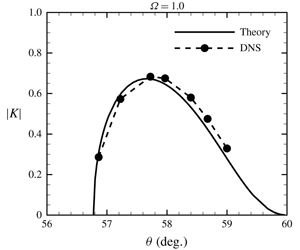The theoretical predictions, obtained assuming $R\gg 1$, are found to be in quantitative agreement with the DNS results at moderate values of $R$ when the roughness elements are located near the lower branch of the instability. The receptivity is sensitive to the incident angle (or the phase speed) of the acoustic wave, being highly effective within a small range of angles close to $\cos ^{-1}(1/M)$ and $\unicode[STIX]{x03C0}+\cos ^{-1}(1/M)$ for downstream and upstream propagating sound waves, respectively. The amplitude of the instability mode excited is proportional to the streamwise-velocity amplitude of the acoustic signature inside the boundary layer, and scales with the roughness height $h^{\ast }$ as $(h^{\ast }/\unicode[STIX]{x1D6FF}^{\ast })R^{1/4}$, where $\unicode[STIX]{x1D6FF}^{\ast }$ is the boundary-layer thickness.

JFM classification

Boundary Layers: Boundary layer receptivity Instability: Transition to turbulence Boundary Layers: Boundary layer stability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 888 , 10 April 2020 , A10
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions. National Bureau of Standards.Google Scholar
Balakumar, P.2003 Transition in a supersonic boundary-layer due to roughness and acoustic disturbances. AIAA Paper 2003-3589.CrossRefGoogle Scholar
Balakumar, P.2005 Transition in a supersonic boundary layer due to acoustic disturbances. AIAA Paper 2005-96.CrossRefGoogle Scholar
Balakumar, P.2006 Stability of supersonic boundary layers over blunt wedges. AIAA Paper 2006-3053.CrossRefGoogle Scholar
Balakumar, P. 2009 Receptivity of a supersonic boundary layer to acoustic disturbances. AIAA J. 47 (5), 1069–1078.CrossRefGoogle Scholar
Balakumar, P.2015 Receptivity of hypersonic boundary layers to acoustic and vortical disturbances (invited). AIAA Paper 2015-2473.CrossRefGoogle Scholar
Balakumar, P. & Malik, M. R. 1992 Discrete modes and continuous spectra in supersonic boundary layers. J. Fluid Mech. 239, 631–656.CrossRefGoogle Scholar
Choudhari, M. & Kerschen, E. J.1990 Instability wave patterns generated by interaction of sound waves with three-dimensional wall suction or roughness. AIAA Paper 90-0119.CrossRefGoogle Scholar
Choudhari, M. & Streett, C. L. 1992 A finite Reynolds-number approach for the prediction of boundary-layer receptivity in localized regions. Phys. Fluids A 4 (11), 2495–2514.CrossRefGoogle Scholar
Cowley, S. J. & Hall, P. 1990 On the instability of hypersonic flow past a wedge. J. Fluid Mech. 214, 17–42.CrossRefGoogle Scholar
Crouch, J. D. 1992 Localized receptivity of boundary layers. Phys. Fluids A 4, 1408–1414.CrossRefGoogle Scholar
De Tullio, N. & Ruban, A. I. 2015 A numerical evaluation of the asymptotic theory of receptivity for subsonic compressible boundary layers. J. Fluid Mech. 771, 520–546.CrossRefGoogle Scholar
Dietz, A. J. 1999 Local boundary-layer receptivity to a convected free-stream disturbance. J. Fluid Mech. 378, 291–317.CrossRefGoogle Scholar
Duck, P. W., Lasseigne, D. G. & Hussaini, M. Y. 1995 On the interaction between the shock wave attached to a wedge and freestream disturbances. Theor. Comput. Fluid Dyn. 7 (2), 119–139.CrossRefGoogle Scholar
Duck, P. W., Lasseigne, D. G. & Hussaini, M. Y. 1997 The effect of three-dimensional freestream disturbances on the supersonic flow past a wedge. Phys. Fluids 9 (2), 456–467.CrossRefGoogle Scholar
Duck, P. W., Ruban, A. I. & Zhikharev, C. N. 1996 The generation of Tollmien–Schlichting waves by free-stream turbulence. J. Fluid Mech. 312, 341–371.CrossRefGoogle Scholar
Fedorov, A. V. 2003a Receptivity of a high-speed boundary layer to acoustic disturbances. J. Fluid Mech. 491, 101–129.CrossRefGoogle Scholar
Fedorov, A. V.2003b Receptivity of hypersonic boundary layer to acoustic disturbances scattered by surface roughness. AIAA Paper 2003-3731.CrossRefGoogle Scholar
Fedorov, A. V. 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43 (1), 79–95.CrossRefGoogle Scholar
Fedorov, A. V. & Khokhlov, A. P. 1991 Excitation of unstable modes in a supersonic boundary layer by acoustic waves. Fluid Dyn. 26 (4), 531–537.CrossRefGoogle Scholar
Fedorov, A. V. & Khokhlov, A. P. 2001 Prehistory of instability in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 14 (6), 359–375.CrossRefGoogle Scholar
Goldstein, M. E. 1983 The evolution of Tollmien–Schlichting waves near a leading edge. J. Fluid Mech. 127, 59–81.CrossRefGoogle Scholar
Goldstein, M. E. 1985 Scattering of acoustic waves into Tollmien–Schlichting waves by small streamwise variations in surface geometry. J. Fluid Mech. 154, 509–529.CrossRefGoogle Scholar
Goldstein, M. E. & Hultgren, L. S. 1989 Boundary-layer receptivity to long-wave free-stream disturbances. Annu. Rev. Fluid Mech. 21, 137–166.CrossRefGoogle Scholar
Goldstein, M. E. & Ricco, P. 2018 Non-localized boundary layer instabilities resulting from leading edge receptivity at moderate supersonic Mach numbers. J. Fluid Mech. 838, 435–477.CrossRefGoogle Scholar
Hernández, C. G. & Wu, X. 2019 Receptivity of supersonic boundary layers over smooth and wavy surfaces to impinging slow acoustic waves. J. Fluid Mech. 872, 849–888.CrossRefGoogle Scholar
Kachanov, Y. S. 1994 Physical mechanisms of laminar-boundary-layer transition. Annu. Rev. Fluid Mech. 26, 411–482.CrossRefGoogle Scholar
King, R. A. & Breuer, K. S. 2001 Acoustic receptivity and evolution of two-dimensional and oblique disturbances in a Blasius boundary layer. J. Fluid Mech. 432, 69–90.CrossRefGoogle Scholar
Laufer, J. 1961 Aerodynamic noise in supersonic wind tunnels. J. Aero. Sci. 28, 685–692.Google Scholar
Lin, C. C. 1946 On the stability of two-dimensional parallel flows. Part III. Stability in a viscous fluid. Q. Appl. Maths 3 (4), 277–301.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2003a Receptivity of a supersonic boundary layer over a flat plate. Part 1. Wave structures and interactions. J. Fluid Mech. 488, 31–78.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2003b Receptivity of a supersonic boundary layer over a flat plate. Part 2. Receptivity to free-stream sound. J. Fluid Mech. 488, 79–121.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2005 Receptivity of a supersonic boundary layer over a flat plate. Part 3. Effects of different types of free-stream disturbances. J. Fluid Mech. 532, 63–109.CrossRefGoogle Scholar
Mack, L. M.1984 Boundary-layer linear stability theory. AGARD Rep. 709.Google Scholar
Malik, M. R. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86, 376–413.CrossRefGoogle Scholar
Maslov, A. A., Mironov, S. G., Kudryavtsev, A. N., Poplavskaya, T. V. & Tsyryulnikov, I. S. 2010 Wave processes in a viscous shock layer and control of fluctuations. J. Fluid Mech. 650, 81–118.CrossRefGoogle Scholar
Maslov, A. A., Shiplyuk, A. N., Sidorenko, A. A. & Arnal, D. 2001 Leading-edge receptivity of a hypersonic boundary layer on a flat plate. J. Fluid Mech. 426, 73–94.CrossRefGoogle Scholar
Mengaldo, G., Kravtsova, M., Ruban, A. I. & Sherwin, S. J. 2015 Triple-deck and direct numerical simulation analyses of high-speed subsonic flows past a roughness element. J. Fluid Mech. 774, 311–323.CrossRefGoogle Scholar
Morkovin, M. V.1969 Critical evaluation of transition from laminar to turbulent shear layers with emphasis on hypersonically travelling bodies. Tech. Rep. AFFDL-TR, pp. 68–149.Google Scholar
Poinsot, T. J. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101, 104–129.CrossRefGoogle Scholar
Qin, H. & Dong, M. 2016 Boundary-layer disturbances subjected to free-stream turbulence and simulation on bypass transition. Z. Angew. Math. Mech. 37 (8), 967–986.CrossRefGoogle Scholar
Qin, F. & Wu, X. 2016 Response and receptivity of the hypersonic boundary layer past a wedge to free-stream acoustic, vortical and entropy disturbances. J. Fluid Mech. 797, 874–915.CrossRefGoogle Scholar
Ruban, A. I. 1984 On Tollmien–Schlichting wave generation by sound. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 5, 44–52 (English translation: Fluid Dyn. 19, 709–717 (1985)).Google Scholar
Saric, W. S., Hoos, J. A. & Radeztsky, R. H. 1991 Boundary-layer receptivity of sound with roughness. In Boundary Layer Stability and Transition to Turbulence (ed. Reda, D. C., Reed, H. L. & Kobayashi, R.), FED, vol. 114, pp. 17–22. ASME.Google Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34, 291–319.CrossRefGoogle Scholar
Schneider, S. P. 2001 Effects of high-speed tunnel noise on laminar-turbulent transition. J. Spacecr. Rockets 38 (3), 323–333.CrossRefGoogle Scholar
Smith, F. T. 1973 Laminar flow over a small hump on a flat plate. J. Fluid Mech. 57, 803–824.CrossRefGoogle Scholar
Smith, F. T. 1979 On the non-parallel flow stability of the Blasius boundary layer. Proc. R. Soc. Lond. A 366 (1724), 91–109.Google Scholar
Smith, F. T. 1989 On the first-mode instability in subsonic, supersonic or hypersonic boundary layers. J. Fluid Mech. 198, 127–153.CrossRefGoogle Scholar
Smith, F. T., Sykes, R. I. & Brighton, P. W. M. 1977 A two-dimensional boundary layer encountering a three-dimensional hump. J. Fluid Mech. 83 (1), 163–176.CrossRefGoogle Scholar
Stewartson, K. 1974 Multistructured boundary layers on flat plates and related bodies. Adv. Appl. Mech. 14, 145–239.CrossRefGoogle Scholar
Wu, X. 1999 Generation of Tollmien–Schlichting waves by convecting gusts interacting with sound. J. Fluid Mech. 397, 285–316.CrossRefGoogle Scholar
Wu, X. 2001a On local boundary-layer receptivity to vortical disturbances in the free stream. J. Fluid Mech. 449, 373–393.CrossRefGoogle Scholar
Wu, X. 2001b Receptivity of boundary layers with distributed roughness to vortical and acoustic disturbances: a second-order asymptotic theory and comparison with experiments. J. Fluid Mech. 431, 91–133.CrossRefGoogle Scholar
Wu, X. 2019 Nonlinear theories for shear flow instabilities: physical insights and practical implications. Annu. Rev. Fluid Mech. 51, 451–485.CrossRefGoogle Scholar
Wu, X. & Zhang, J. 2008 Instability of a stratified boundary layer and its coupling with internal gravity waves. Part 2. Coupling with internal gravity waves via topography. J. Fluid Mech. 595, 409–433.CrossRefGoogle Scholar
Würz, W., Herr, S., Wörner, A., Rist, U., Wagner, S. & Kachanov, Y. S. 2003 Three-dimensional acoustic-roughness receptivity of a boundary layer on an airfoil: experiment and direct numerical simulations. J. Fluid Mech. 478, 135–163.CrossRefGoogle Scholar
Zhigulev, V. N. & Fedorov, A. V. 1987 Boundary-layer receptivity to acoustic disturbances. J. Appl. Mech. Tech. Phys. 28 (1), 28–34.CrossRefGoogle Scholar
Zhong, X. 2001 Leading-edge receptivity to free-stream disturbance waves for hypersonic flow over a parabola. J. Fluid Mech. 441, 315–367.CrossRefGoogle Scholar
Zhong, X. & Ma, Y. 2006 Boundary-layer receptivity of Mach 7.99 flow over a blunt cone to free-stream acoustic waves. J. Fluid Mech. 556, 55–103.CrossRefGoogle Scholar
Zhong, X. & Wang, X. 2012 Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers. Annu. Rev. Fluid Mech. 44 (1), 527–561.CrossRefGoogle Scholar
Zhou, M. D., Liu, D. P. & Blackwelder, R. F. 1994 An experimental study of receptivity of acoustic waves in laminar boundary layers. Exp. Fluids 17, 1–9.CrossRefGoogle Scholar