Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T15:18:43.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Generation mechanism of a hierarchy of vortices in a turbulent boundary layer

Published online by Cambridge University Press:  28 February 2019

Yutaro Motoori  and
Susumu Goto Open the ORCID record for Susumu Goto [Opens in a new window]
Yutaro Motoori*
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka, 560-8531, Japan
Susumu Goto*
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka, 560-8531, Japan
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

To understand the generation mechanism of a hierarchy of multiscale vortices in a high-Reynolds-number turbulent boundary layer, we conduct direct numerical simulations and educe the hierarchy of vortices by applying a coarse-graining method to the simulated turbulent velocity field. 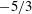When the Reynolds number is high enough for the premultiplied energy spectrum of the streamwise velocity component to show the second peak and for the energy spectrum to obey the $-5/3$ power law, small-scale vortices, that is, vortices sufficiently smaller than the height from the wall, in the log layer are generated predominantly by the stretching in strain-rate fields at larger scales rather than by the mean-flow stretching. In such a case, the twice-larger scale contributes most to the stretching of smaller-scale vortices. This generation mechanism of small-scale vortices is similar to the one observed in fully developed turbulence in a periodic cube and consistent with the picture of the energy cascade. On the other hand, large-scale vortices, that is, vortices as large as the height, are stretched and amplified directly by the mean flow. We show quantitative evidence of these scale-dependent generation mechanisms of vortices on the basis of numerical analyses of the scale-dependent enstrophy production rate. We also demonstrate concrete examples of the generation process of the hierarchy of multiscale vortices.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 1085 - 1109
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. Trans. ASME J. Fluids Engng 126, 835–843.10.1115/1.1789528Google Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.10.1063/1.2717527Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.10.1017/S0022112000001580Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.10.1017/S0022112006000814Google Scholar
Amsden, A. A. & Harlow, F. H. 1970 A simplified MAC technique for incompressible fluid flow calculations. J. Comput. Phys. 6, 322–325.10.1016/0021-9991(70)90029-XGoogle Scholar
Borrell, G., Sillero, J. A. & Jiménez, J. 2013 A code for direct numerical simulation of turbulent boundary layers at high Reynolds numbers in BG/P supercomputers. Comput. Fluid 80, 37–43.10.1016/j.compfluid.2012.07.004Google Scholar
Cardesa, J. I., Vela-Martin, A. & Jiménez, J. 2017 The turbulent cascade in five dimensions. Science 357, 782–784.Google Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.10.1017/S0022112097008057Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.10.1017/S0022112001003512Google Scholar
Cimarelli, A., De Angelis, E., Jiménez, J. & Casciola, C. M. 2016 Cascades and wall-normal fluxes in turbulent channel flows. J. Fluid Mech. 796, 417–436.Google Scholar
Corrsin, S. 1958 Local isotropy in turbulent shear flow. NACA RM 58B11.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.10.1017/S0022112010006324Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.Google Scholar
Eitel-Amor, G., Örlü, R., Schlatter, P. & Flores, O. 2015 Hairpin vortices in turbulent boundary layers. Phys. Fluids 27, 025108.10.1063/1.4907783Google Scholar
Frisch, U. 1995 Turbulence, The Legacy of A. N. Kolmogorov. Cambridge University Press.10.1017/CBO9781139170666Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Goto, S. 2008 A physical mechanism of the energy cascade in homogeneous isotropic turbulence. J. Fluid Mech. 605, 355–366.10.1017/S0022112008001511Google Scholar
Goto, S. 2012 Coherent structures and energy cascade in homogeneous turbulence. Progr. Theor. Phys. Suppl. 195, 139–156.10.1143/PTPS.195.139Google Scholar
Goto, S., Saito, Y. & Kawahara, G. 2017 Hierarchy of antiparallel vortex tubes in spatially periodic turbulence at high Reynolds numbers. Phys. Rev. Fluids 2, 064603.10.1103/PhysRevFluids.2.064603Google Scholar
Hambleton, W. T., Hutchins, N. & Marusic, I. 2006 Simultaneous orthogonal-plane particle image velocimetry measurements in a turbulent boundary layer. J. Fluid Mech. 560, 53–64.10.1017/S0022112006000292Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.10.1017/S0022112086001192Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145, 273–306.10.1007/s10546-012-9735-4Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hwang, J., Lee, J., Sung, H. J. & Zaki, T. A. 2016 Inner–outer interactions of large-scale structures in turbulent channel flow. J. Fluid Mech. 790, 128–157.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.10.1017/jfm.2015.24Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.10.1146/annurev-fluid-120710-101039Google Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25, 101302.10.1063/1.4824988Google Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, 1–100.10.1017/jfm.2018.144Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Jodai, Y. & Elsinga, G. E. 2016 Experimental observation of hairpin auto-generation events in a turbulent boundary layer. J. Fluid Mech. 795, 611–633.10.1017/jfm.2016.153Google Scholar
Kajishima, T. & Taira, K. 2017 Computational Fluid Dynamics. Springer.10.1007/978-3-319-45304-0Google Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.10.1063/1.869889Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Lee, J., Jung, S. Y., Sung, H. J. & Zaki, T. A. 2013 Effect of wall heating on turbulent boundary layers with temperature-dependent viscosity. J. Fluid Mech. 726, 196–225.10.1017/jfm.2013.211Google Scholar
Lee, J., Lee, J. H., Choi, J. & Sung, H. J. 2014 Spatial organization of large- and very-large-scale motions in a turbulent channel flow. J. Fluid Mech. 749, 818–840.10.1017/jfm.2014.249Google Scholar
Lee, J., Sung, H. J. & Zaki, T. A. 2017 Signature of large-scale motions on turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 819, 165–187.10.1017/jfm.2017.170Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.10.1017/S002211201000621XGoogle Scholar
Leung, T., Swaminathan, N. & Davidson, P. A. 2012 Geometry and interaction of structures in homogeneous isotropic turbulence. J. Fluid Mech. 710, 453–481.10.1017/jfm.2012.373Google Scholar
Lozano-Durán, A., Holzner, M. & Jiménez, J. 2016 Multiscale analysis of the topological invariants in the logarithmic region of turbulent channels at a friction Reynolds number of 932. J. Fluid Mech. 803, 356–394.Google Scholar
Marusic, I. & Hutchins, N. 2008 Study of the log-layer structure in wall turbulence over a very large range of Reynolds number. Flow. Turbul. Combust. 81, 115–130.Google Scholar
Melander, M. V. & Hussain, F. 1993 Coupling between a coherent structure and fine-scale turbulence. Phys. Rev. E 48, 2669–2689.Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2008 Comparison of mean flow similarity laws in zero pressure gradient turbulent boundary layers. Phys. Fluids 20, 105102.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanics of wall turbulence. J. Fluid Mech. 119, 173–217.10.1017/S0022112082001311Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.10.1017/S0022112095003351Google Scholar
Robinson, S. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.10.1146/annurev.fl.23.010191.003125Google Scholar
Schlatter, P., Li, Q., Örlü, R., Hussain, F. & Henningson, D. S. 2014 On the near-wall vortical structures at moderate Reynolds numbers. Eur. J. B 48, 75–93.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.10.1017/S0022112010003113Google Scholar
Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.Google Scholar
Tennekes, K. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proceedings of the Midwest Conference in Fluid Mechanics. Ohio State University.Google Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.10.1017/S002211200400237XGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.10.1017/S0022112003005251Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Wu, X. 2017 Inflow turbulence generation methods. Annu. Rev. Fluid Mech. 49, 23–49.10.1146/annurev-fluid-010816-060322Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.10.1017/S0022112009006624Google Scholar