Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-04T21:37:01.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Generation and characteristics of vortex rings free of piston vortex and stopping vortex effects

Published online by Cambridge University Press:  06 December 2016

Debopam Das ,
M. Bansal  and
A. Manghnani
Debopam Das*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur 208016, India
M. Bansal
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur 208016, India
A. Manghnani
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur 208016, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents a novel method for generating vortex rings that circumvents some of the drawbacks associated with existing methods in producing them. The predominant effects that occur in previously used methods are due to the presence of some of the other vortices such as the stopping vortex, piston vortex, image vortex and orifice lip generated vortices in the early stage of development. These disturbances influence the geometric, kinematic and dynamic characteristics of a vortex ring and lead to mismatches with classical theoretical predictions. It is shown in the present study that the disturbance free vortex rings produced follow the classical theory. 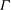Flow visualization and particle image velocimetry experiments are carried out in the Reynolds number (defined as the ratio of circulation ($\unicode[STIX]{x1D6E4}$) and kinematic viscosity ($\unicode[STIX]{x1D708}$)) range, 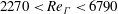$2270<Re_{\unicode[STIX]{x1D6E4}}<6790$, to find the translational velocity, total and core circulation, core diameter, ring diameter and bubble diameter. In reference to the earlier studies, significant differences are noted in the variations of the vortex ring diameter and core diameter. A model for the core diameter during the formation stage is proposed. The translational velocity variation with time shows that the second-order accurate formula derived using Hamilton’s equation by Fraenkel (J. Fluid Mech., vol. 51, 1972, pp. 119–135) predicts it best.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 811 , 25 January 2017 , pp. 138 - 167
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhmetov, D. G. 2008 Model of vortex ring formation. J. Appl. Mech. Tech. Phys. 49 (6), 909–918.CrossRefGoogle Scholar
Allen, J. J. & Auvity, B. 2002 Interaction of a vortex ring with a piston vortex. J. Fluid Mech. 465, 353–378.CrossRefGoogle Scholar
Arakeri, J. H., Das, D., Krothapalli, A. & Lourenco, L. 2004 Vortex ring formation at the open end of a shock tube: a particle image velocimetry study. Phys. Fluids 16, 1008–1019.CrossRefGoogle Scholar
Auerbach, D. 1987 Experiments on the trajectory and circulation of the starting vortex. J. Fluid Mech. 183, 185–198.CrossRefGoogle Scholar
Auerbach, D. 1991 Stirring properties of vortex rings. Phys. Fluids A 3, 1351.CrossRefGoogle Scholar
Babbage, C. 1864 Passages from the Life of a Philosopher. Longman.Google Scholar
Blondeaux, P. & De Bernardinis, B. 1983 On the formation of vortex pairs near orifices. J. Fluid Mech. 135, 111–122.CrossRefGoogle Scholar
Cater, J. E., Soria, J. & Lim, T. T. 2004 The interaction of the piston vortex with a piston-generated vortex ring. J. Fluid Mech. 499 (1), 327–343.CrossRefGoogle Scholar
Dabiri, J. O. & Gharib, M. 2004 Fluid entrainment by isolated vortex rings. J. Fluid Mech. 511 (1), 311–331.CrossRefGoogle Scholar
Das, D.1998 Evolution and instability of unsteady boundary-layers with reverse flow. PhD thesis, Indian Institute of Science Bangalore.Google Scholar
Das, D. & Arakeri, J. H. 1998 Transition of unsteady velocity profiles with reverse flow. J. Fluid Mech. 374, 251–283.CrossRefGoogle Scholar
Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. Zeitschrift für angewandte Mathematik und Physik ZAMP 30 (1), 101–116.CrossRefGoogle Scholar
Donnelly, R. J. 1991 Quantized Vortices in Helium II. Cambridge University Press.Google Scholar
Faraday, M. 1847 On the steam jet. J. Franklin Inst. 44, 212–213.CrossRefGoogle Scholar
Fraenkel, L. E. 1972 Examples of steady vortex rings of small cross-section in an ideal fluid. J. Fluid Mech. 51, 119–135.CrossRefGoogle Scholar
Fuentes, O. V. 2014 Early observations and experiments on ring vortices. Eur. J. Mech. (B/Fluids) 43, 166–171.CrossRefGoogle Scholar
Fukumoto, Y. & Moffatt, H. K. 2000 Motion and expansion of a viscous vortex ring. Part 1. A higher-order asymptotic formula for the velocity. J. Fluid Mech. 417, 1–45.CrossRefGoogle Scholar
Gengembre, P. 1785 Sur un nouveau gaz obtenu par l’action des alkalis sur le phosphore de kunckel. Obs. Phys. Hist. Nat. Arts 27, 276–281.Google Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids 31 (12), 3532–3542.CrossRefGoogle Scholar
Glezer, A. & Coles, D. 1990 An experimental study of a turbulent vortex ring. J. Fluid Mech. 211 (1), 243–283.CrossRefGoogle Scholar
Irdmusa, J. Z. & Garris, C. A. 1987 Influence of initial and boundary conditions on vortex ring development. AIAA J. 25 (3), 371–372.CrossRefGoogle Scholar
Kaden, H. 1931 Aufwicklung einer unstabilen unstetigkeitsfliiche. Ing.-Arch. 2, 140–168.CrossRefGoogle Scholar
Krueger, P. S. 2005 An over-pressure correction to the slug model for vortex ring circulation. J. Fluid Mech. 545, 427–443.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Lim, T. T. & Nickels, T. B. 1995 Vortex rings. In Fluid Vortices, pp. 95–153. Springer.CrossRefGoogle Scholar
Maxworthy, T. 1972 The structure and stability of vortex rings. J. Fluid Mech. 51 (1), 15–32.CrossRefGoogle Scholar
Maxworthy, T. 1977 Some experimental studies of vortex rings. J. Fluid Mech. 81 (03), 465–495.CrossRefGoogle Scholar
Pedrizzetti, G. 2010 Vortex formation out of two-dimensional orifices. J. Fluid Mech. 655, 198–216.CrossRefGoogle Scholar
Pullin, D. I. 1979 Vortex ring formation at tube and orifice openings. Phys. Fluids 22, 401.CrossRefGoogle Scholar
Pullin, D. I. & Perry, A. E. 1980 Some flow visualization experiments on the starting vortex. J. Fluid Mech. 97 (2), 239–255.CrossRefGoogle Scholar
Rogers, W. B. 1858 On the formation of rotating rings by air and liquids under certain conditions of discharge. Am. J. Sci. 26, 246–258.Google Scholar
Saffman, P. G. 1978 The number of waves on unstable vortex rings. J. Fluid Mech. 84 (04), 625–639.CrossRefGoogle Scholar
Saffman, Po. G. 1970 The velocity of viscous vortex rings (small cross section viscous vortex ring velocity in ideal fluid with arbitrary vorticity distribution in core). Stud. Appl. Math. 49, 371–380.CrossRefGoogle Scholar
Shusser, M. & Gharib, M. 2000 Energy and veocity of a formaing vortex ring. Phys. Fluids 12, 618–621.CrossRefGoogle Scholar
Shusser, M., Gharib, M., Rosenfeld, M. & Mohseni, K. 2002 On the effect of pipe boundary layer growth on the formation of a laminar vortex ring generated by a piston/cylinder arrangement. Theor. Comput. Fluid Dyn. 15, 618–621.CrossRefGoogle Scholar
Sullivan, I. S., Niemela, J. J., Hershberger, R. E, Bolster, D. & Donnelly, R. J. 2008 Dynamics of thin vortex rings. J. Fluid Mech. 609, 319.CrossRefGoogle Scholar
Tung, C. & Ting, L. 1967 Motion and decay of a vortex ring. Phys. Fluids 10 (5), 901.CrossRefGoogle Scholar
Weigand, A. & Gharib, M. 1997 On the evolution of laminar vortex rings. Exp. Fluids 22 (6), 447–457.CrossRefGoogle Scholar