Article contents
A generalized vortex ring model
Published online by Cambridge University Press: 10 March 2009
Abstract
A conventional laminar vortex ring model is generalized by assuming that the time dependence of the vortex ring thickness ℓ is given by the relation ℓ = atb, where a is a positive number and 1/4 ≤ b ≤ 1/2. In the case in which 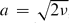 , where ν is the laminar kinematic viscosity, and b = 1/2, the predictions of the generalized model are identical with the predictions of the conventional laminar model. In the case of b = 1/4 some of its predictions are similar to the turbulent vortex ring models, assuming that the time-dependent effective turbulent viscosity ν∗ is equal to ℓℓ′. This generalization is performed both in the case of a fixed vortex ring radius R0 and increasing vortex ring radius. In the latter case, the so-called second Saffman's formula is modified. In the case of fixed R0, the predicted vorticity distribution for short times shows a close agreement with a Gaussian form for all b and compares favourably with available experimental data. The time evolution of the location of the region of maximal vorticity and the region in which the velocity of the fluid in the frame of reference moving with the vortex ring centroid is equal to zero is analysed. It is noted that the locations of both regions depend upon b, the latter region being always further away from the vortex axis than the first one. It is shown that the axial velocities of the fluid in the first region are always greater than the axial velocities in the second region. Both velocities depend strongly upon b. Although the radial component of velocity in both of these regions is equal to zero, the location of both of these regions changes with time. This leads to the introduction of an effective radial velocity component; the latter case depends upon b. The predictions of the model are compared with the results of experimental measurements of vortex ring parameters reported in the literature.
, where ν is the laminar kinematic viscosity, and b = 1/2, the predictions of the generalized model are identical with the predictions of the conventional laminar model. In the case of b = 1/4 some of its predictions are similar to the turbulent vortex ring models, assuming that the time-dependent effective turbulent viscosity ν∗ is equal to ℓℓ′. This generalization is performed both in the case of a fixed vortex ring radius R0 and increasing vortex ring radius. In the latter case, the so-called second Saffman's formula is modified. In the case of fixed R0, the predicted vorticity distribution for short times shows a close agreement with a Gaussian form for all b and compares favourably with available experimental data. The time evolution of the location of the region of maximal vorticity and the region in which the velocity of the fluid in the frame of reference moving with the vortex ring centroid is equal to zero is analysed. It is noted that the locations of both regions depend upon b, the latter region being always further away from the vortex axis than the first one. It is shown that the axial velocities of the fluid in the first region are always greater than the axial velocities in the second region. Both velocities depend strongly upon b. Although the radial component of velocity in both of these regions is equal to zero, the location of both of these regions changes with time. This leads to the introduction of an effective radial velocity component; the latter case depends upon b. The predictions of the model are compared with the results of experimental measurements of vortex ring parameters reported in the literature.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2009
References
REFERENCES
- 29
- Cited by


