2.1. Problem

Consider a rarefied gas in the annulus between eccentric circular cylinders as shown in figure 1(a). The radius of the inner cylinder is $r_a$, that of the outer cylinder is $r_b$, and the distance between the two axes is $e_c$. The inner cylinder rotates at a constant circumferential speed $v_w$, and the outer cylinder is at rest. The temperature of the cylinders is a constant $T_0$. The dimensionless curvature $c$ is defined by $c=(r_b-r_a)/r_a$. The rarefaction parameter $k$ is defined by $k=(\sqrt {{\rm \pi} }/2)\ell /(r_b-r_a)$, where $\ell$ is the mean free path of the gas in the equilibrium state at rest with the average density $\rho _0$ of the gas and the temperature $T_0$; we call $k$ the Knudsen number for simplicity. In the literature on lubrication, the Knudsen number $k_n=(\sqrt {{\rm \pi} }/2)\ell /(r_b-r_a-e_c)$ based on the narrowest clearance $r_b-r_a-e_c$ is also used. This $k_n$ is related to $k$ here by $k_n=(1-\varepsilon )^{-1}k$. Let $c$ be small, and let the circumferential speed $v_w$ of rotation also be small. The eccentricity $\varepsilon =e_c/(r_b-r_a)$ is arbitrary, but it is not close to unity. To be specific

(2.1a–c)\begin{equation} c \ll 1,\quad \frac{v_w}{(2RT_0)^{1/2}}= \hat{v}_w= c u_w,\quad 1-\varepsilon=O(1), \end{equation}

where $R$ is the specific gas constant, i.e. the Boltzmann constant divided by the mass of a molecule, and $u_w$ is a constant of the order of unity. Equation (2.1b) implies that the Mach number based on the circumferential speed $v_w$ is of the same order as $c$. The Knudsen number $k$ is arbitrary. We study the time-independent and axially uniform behaviour of the gas on the basis of the Boltzmann equation. We also assume that the gas molecules undergo diffuse reflection on the surfaces of the cylinders.

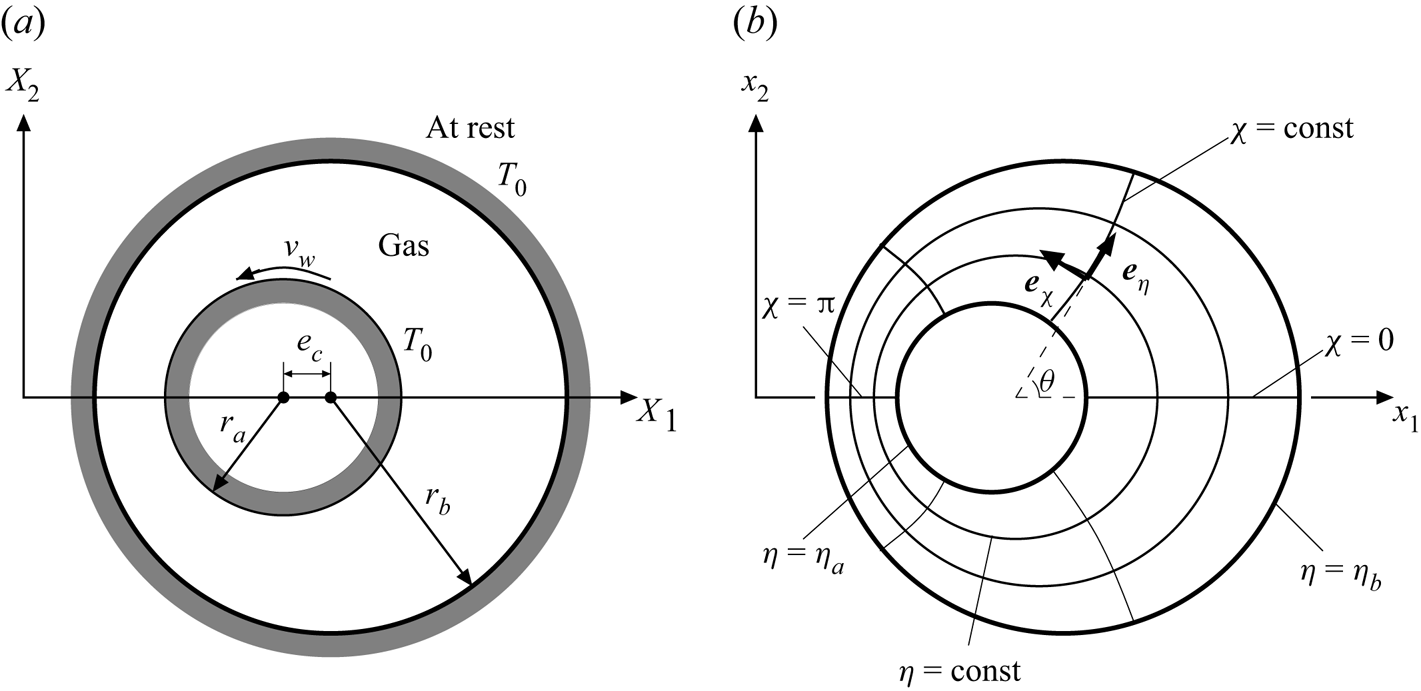
Figure 1. Schematic of the system. (a) Schematic view of the annulus and (b) the bipolar coordinate system ($\eta, \chi$) in the dimensionless space.

2.2. Basic equation

We introduce the dimensionless variables

(2.2a,b)\begin{equation} x_i=\frac{X_i}{r_b-r_a}, \quad \zeta_i=\frac{\xi_i}{(2RT_0)^{1/2}}, \end{equation}

for the spatial rectangular coordinates $X_i$ and the molecular velocity $\xi _i$. The dimensionless molecular velocity $\zeta _i$ is also denoted by $\boldsymbol {\zeta }$.

In the following analysis, we use the bipolar coordinate system $\eta, \chi, \zeta _\eta, \zeta _\chi, \zeta _z$, as shown in figure 1(b), defined by

(2.3a,b)$$\begin{gather} x_1={-}\frac{a \sinh \eta}{\cosh\eta -\cos\chi}, \quad x_2= \frac{a \sin \chi}{\cosh\eta -\cos\chi}, \end{gather}$$

(2.4)$$\begin{gather}\boldsymbol{\zeta}= \zeta_\eta\boldsymbol{e}_\eta +\zeta_\chi\boldsymbol{e}_\chi +\zeta_z\boldsymbol{e}_z, \end{gather}$$

where

(2.5)\begin{equation} a= (c\varepsilon)^{{-}1}\left[(1-\varepsilon^2) \left(1+c+\frac{1-\varepsilon^2}{4}c^2\right)\right]^{1/2}. \end{equation}

The scale factor $h$ defined by $h=[(\partial x_1/\partial \eta )^2 +(\partial x_2/\partial \eta )^2]^{1/2} =[(\partial x_1/\partial \chi )^2 +(\partial x_2/\partial \chi )^2]^{1/2}$ is given by

(2.6)\begin{equation} h=\frac{a}{\cosh\eta -\cos\chi}. \end{equation}

The values of $\eta$ and $\chi$ are in the ranges $\eta _a\le \eta \le \eta _b,\ 0\le \chi < 2{\rm \pi}$, where $\eta _a$ and $\eta _b$ are negative constants

(2.7a,b)\begin{equation} \eta_a={-}\text{arcsinh} ca,\quad \eta_b={-}\text{arcsinh} \frac{ca}{1+c},\quad \eta_a<\eta_b<0. \end{equation}

The vectors $\boldsymbol {e}_\eta$ and $\boldsymbol {e}_\chi$ are unit vectors in the $x_1-x_2$ plane normal to the curves $\eta =\text {const}$ and $\chi =\text {const}$, respectively, and $\boldsymbol {e}_z=\boldsymbol {e}_\eta \times \boldsymbol {e}_\chi$. Note that $ca=\varepsilon ^{-1}(1-\varepsilon ^2)^{1/2}+O(c)$ from (2.5). The dimensionless variable $\hat {f}$ for the velocity distribution function $f$ is defined by

(2.8)\begin{equation} \,\hat{f}= \frac{f}{\rho_0(2RT_0)^{{-}3/2}}. \end{equation}

The dimensionless Boltzmann equation that governs $\hat {f}(\eta, \chi, \zeta _\eta, \zeta _\chi, \zeta _z)$ in the time-independent state for the axially uniform case is written as (Kogan Reference Kogan1969)

(2.9)\begin{equation} \frac{\zeta_\eta}{h}\frac{\partial\hat{f}}{\partial \eta}+\frac{\zeta_\chi}{h}\frac{\partial\hat{f}}{\partial \chi} +\frac{1}{h^2}\left( \zeta_\chi\frac{\partial h}{\partial \eta} -\zeta_\eta\frac{\partial h}{\partial \chi} \right) \left(\zeta_\chi\frac{\partial\hat{f}}{\partial \zeta_\eta} -\zeta_\eta\frac{\partial\hat{f}}{\partial \zeta_\chi}\right)= \frac{1}{k} \hat{J}(\,\hat{f},\hat{f}). \end{equation}

The $\hat {J}({\cdot },{\cdot })$ is the dimensionless collision integral defined by

(2.10)\begin{align} \left.\begin{gathered} \hat{J}(\,\hat{f},\hat{g})= \frac{1}{2}\iint \left[ \hat{f}(\boldsymbol{\zeta}^\prime_*) \hat{g}(\boldsymbol{\zeta}^\prime) +\hat{f}(\boldsymbol{\zeta}^\prime)\hat{g}(\boldsymbol{\zeta}^\prime_*) -\hat{f}(\boldsymbol{\zeta}_*) \hat{g}(\boldsymbol{\zeta}) -\hat{f}(\boldsymbol{\zeta})\hat{g}(\boldsymbol{\zeta}_*)\right] \hat{B} \,\text{d} \varOmega(\boldsymbol{e})\,\mathbf{d}\boldsymbol{\zeta}_*, \\ \boldsymbol{\zeta}^\prime= \boldsymbol{\zeta} +[\boldsymbol{e}\boldsymbol{\cdot}(\boldsymbol{\zeta}_*-\boldsymbol{\zeta})]\boldsymbol{e},\quad \boldsymbol{\zeta}^\prime_*= \boldsymbol{\zeta}_* -[\boldsymbol{e}\boldsymbol{\cdot}(\boldsymbol{\zeta}_*-\boldsymbol{\zeta})]\boldsymbol{e}, \end{gathered}\right\} \end{align}

where $\boldsymbol {e}$ is a unit vector, $\textrm {d}{\varOmega }(\boldsymbol {e})$ is the solid-angle element in the direction of $\boldsymbol {e}$ and $\mathbf{d}\boldsymbol {\zeta }_*=\textrm {d}\zeta _{\chi *}\, \textrm {d}\zeta _{\eta *}\, \textrm {d}\zeta _{z*}$. The factor $\hat {B}$ is a function of $|\boldsymbol {e}\boldsymbol {\cdot }(\boldsymbol {\zeta }_*-\boldsymbol {\zeta })|/|\boldsymbol {\zeta }_*-\boldsymbol {\zeta }|$ and $|\boldsymbol {\zeta }_*-\boldsymbol {\zeta }|$, and its functional form is determined by the molecular model. In (2.10), the arguments of the spatial variables $\eta$ and $\chi$ are common and are omitted for simplicity. The integration in (2.10) is carried out over the whole direction of $\boldsymbol {e}$ and the whole space of $\boldsymbol {\zeta }$. The range of integration with respect to $\boldsymbol {\zeta }$ is its whole space unless otherwise stated.

The diffuse-reflection boundary condition on the rotating inner cylinder is given by

(2.11)\begin{equation} \left.\begin{gathered} \,\hat{f} = {\rm \pi}^{{-}3/2}\hat{\sigma}_{a} \exp(-\zeta_\eta^2 -(\zeta_\chi-\hat{v}_w)^2 -\zeta_z^2),\quad \zeta_\eta>0,\enspace \eta=\eta_a, \\ \hat{\sigma}_{a}={-}2\sqrt{\rm \pi} \int_{\zeta_\eta<0} \zeta_\eta \hat{f} \,\mathbf{d}\boldsymbol{\zeta},\quad \eta=\eta_a. \end{gathered}\right\} \end{equation}

The boundary condition on the outer cylinder at rest is given by

(2.12)\begin{equation} \left.\begin{gathered} \,\hat{f} =\hat{\sigma}_{b} E, \quad \zeta_\eta <0,\enspace \eta=\eta_b, \\ \hat{\sigma}_{b}= 2\sqrt{\rm \pi} \int_{\zeta_\eta>0} \zeta_\eta \hat{f} \,\mathbf{d}\boldsymbol{\zeta},\quad \eta=\eta_b, \end{gathered}\right\} \end{equation}

where $E={\rm \pi} ^{-3/2} \exp (-\boldsymbol {\zeta }^2)$. The periodic condition with respect to $\chi$ is given by

(2.13)$$\begin{gather} \hat{f}(\eta, 0, \zeta_\eta, \zeta_\chi, \zeta_z) = \hat{f}(\eta, 2{\rm \pi}, \zeta_\eta, \zeta_\chi, \zeta_z),\quad \zeta_\chi>0, \end{gather}$$

(2.14)$$\begin{gather}\hat{f}(\eta, 2{\rm \pi}, \zeta_\eta, \zeta_\chi, \zeta_z) = \hat{f}(\eta, 0, \zeta_\eta, \zeta_\chi, \zeta_z),\quad \zeta_\chi<0. \end{gather}$$

Finally, the average gas density $\rho _0$ is defined by $\int \!\!\!\int \textrm {d} X_1\, \textrm {d} X_2 \int \! f \,\mathbf{d}\boldsymbol {\xi } = {\rm \pi}(r_b^2-r_a^2)\rho _0$, where the spatial integration is conducted over the annulus region in figure 1(a). In terms of the dimensionless quantities, this equation yields

(2.15)\begin{equation} \int_{0}^{2{\rm \pi}} \text{d}\chi \int_{\eta_a}^{\eta_b} \text{d}\eta\, h^2 \int \hat{f} \,\mathbf{d}\boldsymbol{\zeta} = \frac{2{\rm \pi}}{c} \left( 1 +\frac{c}{2} \right). \end{equation}

The macroscopic variables of the gas, i.e. the density $\rho$, the flow velocity $v_i$ $(i=\eta, \chi )$, the temperature $T$, the pressure $p$ and the stress tensor $p_{ij}$ $(i=\eta, \chi ; j=\eta, \chi )$ are defined by the moments of the velocity distribution function $f$. The dimensionless variables $\hat {\rho }=\rho /\rho _0$, $\hat {v}_i=v_i/(2RT_0)^{1/2}$, $\hat {T}=T/T_0$, $\hat {p}=p/p_0$ ($p_0=R\rho _0 T_0$) and $\hat {p}_{ij}=p_{ij}/p_0$ are given by the moments of the dimensionless distribution function $\hat {f}$ as

(2.16a)$$\begin{gather} \hat{\rho} = \int \hat{f} \,\mathbf{d}\boldsymbol{\zeta}, \end{gather}$$

(2.16b)$$\begin{gather}\hat{v}_i = \frac{1}{\hat{\rho}} \int \zeta_i \kern0.06em\hat{f} \,\mathbf{d}\boldsymbol{\zeta}, \quad i=\chi, \eta, \end{gather}$$

(2.16c)$$\begin{gather}\hat{T} = \dfrac{2}{3\hat{\rho}} \int \left[ (\zeta_\eta-\hat{v}_\eta)^2 +(\zeta_\chi-\hat{v}_\chi)^2 +\zeta_z^2\right] \hat{f} \,\mathbf{d}\boldsymbol{\zeta}, \end{gather}$$

(2.16d)$$\begin{gather}\hat{p}= \hat{\rho} \hat{T}, \end{gather}$$

(2.16e)$$\begin{gather}\hat{p}_{ij}= 2\int (\zeta_i-\hat{v}_i)(\zeta_j-\hat{v}_j) \hat{f} \,\mathbf{d}\boldsymbol{\zeta}, \quad i=\eta, \chi;\enspace j=\eta, \chi. \end{gather}$$

Integrating the Boltzmann equation (2.9) over the whole space of $\zeta _\eta, \zeta _\chi$ and $\zeta _z$, we obtain the equation of continuity

(2.17)\begin{equation} \frac{\partial h \hat{\rho} \hat{v}_\eta}{\partial \eta} +\frac{\partial h \hat{\rho} \hat{v}_\chi}{\partial \chi}=0. \end{equation}

The rectangular components $(F_1, F_2)$ of the force and the torque $N$ acting on the inner cylinder per unit depth is given by

(2.18)$$\begin{gather} \frac{1}{p_0 r_a} \begin{pmatrix} F_1 \\ F_2 \end{pmatrix}={-}\int_{0}^{2{\rm \pi}} \begin{pmatrix} \hat{p}_{\eta\eta} \cos\theta -\hat{p}_{\chi\eta} \sin\theta\\ \hat{p}_{\eta\eta} \sin\theta +\hat{p}_{\chi\eta} \cos\theta \end{pmatrix} ch \,\text{d}\chi,\quad \eta=\eta_a, \end{gather}$$

(2.19)$$\begin{gather}\frac{N}{p_0 r_a^2} = \int_{0}^{2{\rm \pi}} \hat{p}_{\chi\eta} ch\, \text{d}\chi,\quad \eta=\eta_a, \end{gather}$$

where $\theta$ is the angle shown in figure 1(b) defined by

(2.20a,b)\begin{equation} \cos\theta= \frac{ \cosh\eta \cos\chi-1}{\cosh\eta -\cos\chi},\quad \sin\theta= \frac{-\sinh\eta \sin\chi }{\cosh\eta -\cos\chi}. \end{equation}

The boundary-value problem given by (2.9)–(2.15) is characterized by the following four dimensionless parameters:

(2.21a–d)\begin{equation} c=\frac{r_b-r_a}{r_a}, \quad \varepsilon=\frac{e_c}{r_b-r_a}, \quad \hat{v}_w=cu_w=\frac{v_w}{(2RT_0)^{1/2}},\quad k=\frac{\sqrt{\rm \pi}}{2} \frac{\ell}{r_b-r_a}. \end{equation}

We study this problem under the condition (2.1a–c).

2.3. Some transformations

For convenience of the analysis, we introduce the change of independent variables from $\eta, \zeta _\eta$ and $\zeta _\chi$ to $y, \zeta _\rho$ and $\theta _\zeta$ as follows (Sugimoto & Sone Reference Sugimoto and Sone1992):

(2.22a–c)\begin{equation} \eta= \eta_a +(\eta_b-\eta_a)y, \quad \zeta_\eta=\zeta_\rho\cos\theta_\zeta, \quad \zeta_\chi=\zeta_\rho\sin\theta_\zeta,\end{equation}

where $0\le y\le 1,\ 0\le \zeta _\rho <\infty$ and $-{\rm \pi} <\theta _\zeta \le {\rm \pi}$. In terms of the new variables $y, \zeta _\rho, \theta _\zeta$ and $\chi$, the boundary-value problem (2.9)–(2.15) is rewritten as follows. The Boltzmann equation is

(2.23)\begin{equation} \frac{\zeta_\rho\cos\theta_\zeta}{\gamma H} \frac{\partial\hat{f}}{\partial y} +c\frac{\zeta_\rho\sin\theta_\zeta}{H} \frac{\partial\hat{f}}{\partial \chi} -c\zeta_\rho G \frac{\partial\hat{f}}{\partial \theta_\zeta}= \frac{1}{k} \hat{J}(\,\hat{f},\hat{f}), \end{equation}

where

(2.24a–c)\begin{align} H=ch=\frac{-\sinh\eta_a}{\cosh\eta -\cos\chi}, \quad G=\frac{-\sinh\eta \sin\theta_\zeta +\sin\chi \cos\theta_\zeta}{-\sinh\eta_a}, \quad \gamma=\frac{\eta_b-\eta_a}{c}. \end{align}

In (2.24a–c) and in what follows, $\eta$ should be understood as $\eta (y)$ by (2.22a). Note that $H, G$ and $\gamma$ are of $O(1)$. The boundary conditions (2.11)–(2.14) and the subsidiary condition (2.15) are transformed into

(2.25)$$\begin{gather} \,\hat{f} = {\rm \pi}^{{-}3/2}\hat{\sigma}_{a} \exp( -\zeta_\rho^2 +2c u_w\zeta_\rho\sin\theta_\zeta -c^2 u_w^2 -\zeta_z^2),\quad \cos\theta_\zeta>0,\enspace y=0, \end{gather}$$

(2.26)$$\begin{gather}\,\hat{f} =\hat{\sigma}_{b} E, \quad \cos\theta_\zeta<0,\enspace y=1, \end{gather}$$

(2.27)\begin{gather} \left.\begin{gathered} \hat{\sigma}_{a}={-}2\sqrt{\rm \pi} \int\!\!\! \int\!\!\! \int_{\cos\theta_\zeta<0} \zeta_\rho^2\cos\theta_\zeta \kern0.06em\hat{f}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z, \quad y=0, \\ \hat{\sigma}_{b}= 2\sqrt{\rm \pi} \int\!\!\! \int\!\!\! \int_{\cos\theta_\zeta>0} \zeta_\rho^2\cos\theta_\zeta \kern0.06em\hat{f}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z, \quad y=1, \end{gathered}\right\} \end{gather}

(2.28)$$\begin{gather} \hat{f}(y, 0, \zeta_\rho, \theta_\zeta, \zeta_z)= \hat{f}(y, 2{\rm \pi}, \zeta_\rho, \theta_\zeta, \zeta_z),\quad \theta_\zeta>0, \end{gather}$$

(2.29)$$\begin{gather}\hat{f}(y, 2{\rm \pi}, \zeta_\rho, \theta_\zeta, \zeta_z) = \hat{f}(y, 0, \zeta_\rho, \theta_\zeta, \zeta_z),\quad \theta_\zeta<0, \end{gather}$$

(2.30)$$\begin{gather}\int_{0}^{2{\rm \pi}} \text{d}\chi \int_{0}^{1} \text{d} y\, H^2 \int\!\!\! \int \!\!\! \int \zeta_\rho \,\hat{f}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z = \frac{2{\rm \pi}}{\gamma}\left(1+\frac{c}{2}\right), \end{gather}$$

where $E={\rm \pi} ^{-3/2}\exp (-\zeta _\rho ^2-\zeta _z^2)$ in the new variables. Here, and in what follows, we use the convention that $\hat {f}(\eta (y), \chi, \zeta _\eta (\zeta _\rho, \theta _\zeta ), \zeta _\chi (\zeta _\rho, \theta _\zeta ), \zeta _z)$ is simply written as $\hat {f}(y, \chi, \zeta _\rho, \theta _\zeta, \zeta _z)$ because no confusion will arise. The ranges of integration with respect to $\zeta _\rho, \theta _\zeta$ and $\zeta _z$ are, respectively, $0<\zeta _\rho <\infty$, $-{\rm \pi} <\theta _\zeta <{\rm \pi}$ and $-\infty <\zeta _z<\infty$ unless otherwise stated.

The macroscopic variables are

(2.31a)$$\begin{gather} \hat{\rho} = \int \!\!\! \int \!\!\! \int \zeta_\rho \,\hat{f}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z, \end{gather}$$

(2.31b)$$\begin{gather}\hat{v}_\eta = \dfrac{1}{\hat{\rho}} \int \!\!\! \int \!\!\! \int \zeta_\rho^2\cos\theta_\zeta \,\hat{f}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z, \end{gather}$$

(2.31c)$$\begin{gather}\hat{v}_\chi = \dfrac{1}{\hat{\rho}} \int \!\!\! \int \!\!\! \int \zeta_\rho^2\sin\theta_\zeta \,\hat{f}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z, \end{gather}$$

(2.31d)$$\begin{gather}\hat{T} = \dfrac{2}{3\hat{\rho}} \int \!\!\! \int \!\!\! \int \zeta_\rho \left[ (\zeta_\rho\cos\theta_\zeta-\hat{v}_\eta)^2 +(\zeta_\rho\sin\theta_\zeta-\hat{v}_\chi)^2 +\zeta_z^2 \right] \hat{f}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z, \end{gather}$$

(2.31e)$$\begin{gather}\hat{p}= \hat{\rho} \hat{T}, \end{gather}$$

(2.31f)$$\begin{gather}\hat{p}_{\eta\eta}= 2\int \!\!\! \int \!\!\! \int \zeta_\rho(\zeta_\rho\cos\theta_\zeta-\hat{v}_\eta)^2 \,\hat{f}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z, \end{gather}$$

(2.31g)$$\begin{gather}\hat{p}_{\chi\eta}= \hat{p}_{\eta\chi}= 2\int \!\!\! \int \!\!\! \int \zeta_\rho(\zeta_\rho\cos\theta_\zeta-\hat{v}_\eta)(\zeta_\rho\sin\theta_\zeta-\hat{v}_\chi) \,\hat{f}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z. \end{gather}$$

Changing the variable $\eta$ into $y$ using (2.22a), integrating (2.17) with respect to $y$ from 0 to 1 and applying the boundary condition (2.25) or (2.26), we obtain the mass conservation law

(2.32)\begin{equation} \frac{\text{d}}{\text{d} \chi}\int_0^1 H \hat{\rho} \hat{v}_\chi\,\text{d} y = 0. \end{equation}

3.1. Preliminary remarks and plan of analysis

We seek a solution of the boundary-value problem (2.23)–(2.30) for small $c$. Note that the second and the third terms on the left-hand side of (2.23) are multiplied by $c$. The third term $-c\zeta _\rho G \partial \hat {f}/\partial \theta _\zeta$, which is peculiar to a curvilinear coordinate system, will be called the curvature term for short. Then, one may consider it feasible to seek a solution using a perturbation by regarding these two terms as higher-order terms. We seek the solution as a power series expansion in $c$

(3.1)\begin{equation} \,\hat{f}= \,\hat{f}_{(0)} +\,\hat{f}_{(1)}c + \cdots. \end{equation}

Substituting (3.1) into the boundary-value problem reduces it to a sequence of boundary-value problems of the Boltzmann equation with only one derivative term with $\partial \hat {f}_{(m)}/\partial y \ (m=0, 1, \ldots )$; other derivative terms with $\partial \hat {f}_{(m)}/\partial \chi$ and $\partial \hat {f}_{(m)}/\partial \theta _\zeta$ will appear as inhomogeneous terms. However, this perturbation analysis results in a lubrication equation that fails to approximate the solution of the Boltzmann equation for large Knudsen numbers. The reason is as follows (Doi Reference Doi2022).

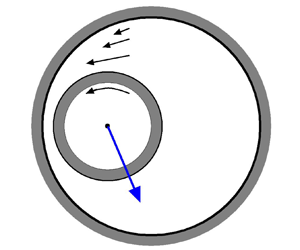
Suppose that the dimensionless curvature $c$ is small but the Knudsen number $k$ is so large that $ck^2=O(1)$. The velocity distribution function will then consist of that of the molecules arriving from the two cylinders without collisions. Figure 2(a) shows a schematic of molecular trajectories arriving at a point from the inner and the outer cylinders. The shaded area represents the range of direction of the molecular velocities arriving from the rotating inner cylinder. It is clear from figure 2(a) that this range from the inner cylinder is smaller than that from the outer cylinder at rest. In figure 2(b), this difference in the angle is denoted by $2\varphi$. From figure 2(b), we see that $\cos \varphi =c^{-1}/(c^{-1}+y)$, and this yields $\varphi \simeq (2yc)^{1/2}$ because $c$ and thus $\varphi$ are small. Thus, the gas behaviour is affected by the curvature by $O(c^{1/2})$ which is much larger than $c$. On the other hand, if we regard the curvature term of (2.23) as a higher-order term, then the characteristics of (2.23) and thus the molecular trajectories are no longer straight, and the angle of the shaded area becomes ${\rm \pi}$ (Doi Reference Doi2022); so the range of direction of the molecular velocities from the rotating inner cylinder is overestimated by an amount proportional to $c^{1/2}$. Thus, simply treating the curvature term as a higher-order term produces a non-negligible error of $O(c^{1/2})$. For example, the macroscopic flow velocity will be estimated to be greater than its actual value. Clearly, this is a non-continuum effect arising from the finite nature of the mean free path. This fact was pointed out in Doi (Reference Doi2022) for a lubrication flow between coaxial cylinders, and an error of $O(c^{1/2})$ was numerically demonstrated. A more detailed discussion is given in Doi (Reference Doi2022). It is quite possible that a similar phenomenon also occurs in the present case of an eccentric annulus.

Figure 2. Characteristics or trajectories of collisionless molecules. (a) Characteristics of the true Boltzmann equation (2.23), where the shaded area represents the range of direction of molecular velocities arriving from the inner cylinder. (b) Schematic showing that the angle of the shaded area in (a) is smaller than ${\rm \pi}$ by $O(c^{1/2})$, specifically, $\varphi \simeq (2yc)^{1/2}$. Note that the dimensionless radius of the inner cylinder is $1/c$.

The above discussion suggests that the key to the correct analysis lies in describing the characteristics of the Boltzmann equation (2.23) correctly. To this end, it is suggested in Doi (Reference Doi2022) that the curvature term should not be treated as a higher-order term but dealt with the first term of (2.23) as a whole, regardless of the magnitude of $c$. Specifically, let us define the operator

(3.2)\begin{equation} \mathcal{D}_{ec}= \frac{\cos\theta_\zeta}{\gamma H}\frac{\partial}{\partial y} -cG\frac{\partial}{\partial \theta_\zeta}. \end{equation}

In terms of $\mathcal {D}_{ec}$, the Boltzmann equation is written as

(3.3)\begin{equation} \zeta_\rho\mathcal{D}_{ec}\,\hat{f} +c\frac{\zeta_\rho\sin\theta_\zeta}{H}\frac{\partial\hat{f}}{\partial \chi} = \frac{1}{k}\hat{J}(\,\hat{f},\hat{f}). \end{equation}

The solution is sought in the power series expansion (3.1). Here, $\mathcal {D}_{ec}$ is not expanded in $c$ but treated as a whole. Namely, we assume

(3.4a,b)\begin{equation} \mathcal{D}_{ec}\,\hat{f} = \mathcal{D}_{ec}\,\hat{f}_{(0)}+\mathcal{D}_{ec}\,\hat{f}_{(1)} c +\cdots,\quad \mathcal{D}_{ec}\,\hat{f}_{(m)}\sim \,\hat{f}_{(m)}\quad (m=0, 1, \ldots). \end{equation}

To be precise, the assumption (3.4b) is inconsistent in the range $|\theta _\zeta -{\rm \pi} /2|=O(c)$. However, it is expected that this discrepancy is localized within a so narrow range in the molecular velocity space that an influence on the macroscopic variable is small (Doi Reference Doi2022). Using this approach, the projection of the characteristics of the Boltzmann equation on the $\theta _\zeta -y$ plane at each stage of approximation is maintained. Substituting (3.1) and (3.4a) into (3.3) and (2.25)–(2.30) and formally arranging the terms of the same order in $c$, we obtain a sequence of boundary-value problems that determine $\hat {f}_{(0)}, \hat {f}_{(1)}, \ldots$ successively from the lowest order as described in the next subsection.

3.2. Leading- and first-order solutions

The boundary-value problem that governs the leading-order solution $\hat {f}_{(0)}$ is given by

(3.5)$$\begin{gather} \zeta_\rho\mathcal{D}_{ec}\kern0.06em\hat{f}_{(0)} = \frac{1}{k} \hat{J}(\,\hat{f}_{(0)}, \,\hat{f}_{(0)}), \end{gather}$$

(3.6)$$\begin{gather}\,\hat{f}_{(0)} = \hat{\sigma}_{a(0)} E, \quad \cos\theta_\zeta>0,\enspace y=0, \end{gather}$$

(3.7)$$\begin{gather}\,\hat{f}_{(0)} = \hat{\sigma}_{b(0)} E, \quad \cos\theta_\zeta<0,\enspace y=1, \end{gather}$$

(3.8)\begin{gather} \left.\begin{gathered} \hat{\sigma}_{a(0)}={-}2\sqrt{\rm \pi} \iint\!\!\!\int_{\cos\theta_\zeta<0} \zeta_\rho^2\cos\theta_\zeta \kern0.06em\hat{f}_{(0)}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z,\quad y=0, \\ \hat{\sigma}_{b(0)}= 2\sqrt{\rm \pi} \iint\!\!\!\int_{\cos\theta_\zeta>0} \zeta_\rho^2\cos\theta_\zeta \kern0.06em\hat{f}_{(0)}\, \text{d}\zeta_\rho\, \text{d}\theta_\zeta\, \text{d}\zeta_z, \quad y=1, \end{gathered}\right\} \end{gather}

(3.9)\begin{gather} \int_0^{2{\rm \pi}} \text{d}\chi \int_{0}^{1}\text{d} y\, H^2 \iint\!\!\! \int \zeta_\rho \kern0.06em\hat{f}_{(0)} \,\text{d}\zeta_\rho \,\text{d}\theta_\zeta \,\text{d}\zeta_z = \frac{2{\rm \pi}}{\gamma}. \end{gather}

Equations (3.5)–(3.7) can be solved independently at each $\chi$ because the derivative term $\partial \hat {f}_{(0)}/\partial \chi$ is absent. A solution is an equilibrium state at rest

(3.10)\begin{equation} \,\hat{f}_{(0)} = C_{(0)} E, \end{equation}

where $C_{(0)}$ may be an arbitrary function of $\chi$ as long as (3.8) is satisfied. The factor $C_{(0)}$ can be related to a macroscopic variable. Substituting the expansion (3.1) into (2.31a)–(2.31e), the macroscopic variables can be expanded in $c$, e.g. $\hat {\rho } = \hat {\rho }_{(0)} + \hat {\rho }_{(1)} c + \cdots$. At the leading order, we obtain from (3.10) that

(3.11a–d)\begin{equation} \hat{\rho}_{(0)} = C_{(0)}, \quad \hat{v}_{\eta(0)} = \hat{v}_{\chi(0)} = 0, \quad \hat{T}_{(0)}=1, \quad \hat{p}_{(0)}= C_{(0)}. \end{equation}

Thus, $C_{(0)}$ is identified with the leading-order pressure $\hat {p}_{(0)}$. We henceforth write $\hat {p}_{(0)}$ for $C_{(0)}$. Incidentally, we obtain $\hat {\sigma }_{a(0)}=\hat {\sigma }_{b(0)}=\hat {p}_{(0)}$ and $\int \!\!\!\int \!\!\! \int \zeta _\rho \hat {f}_{(0)} \,\textrm {d}\zeta _\rho \,\textrm {d}\theta _\zeta \,\textrm {d}\zeta _z=\hat {\rho }_{(0)}=\hat {p}_{(0)}$.

The boundary-value problem for the first-order solution $\hat {f}_{(1)}$ is a linear and inhomogeneous one given by

(3.12)$$\begin{gather} \zeta_\rho\mathcal{D}_{ec}\kern0.06em\hat{f}_{(1)} = \frac{2}{k} \hat{J}(\,\hat{f}_{(0)}, \,\hat{f}_{(1)}) -\frac{\zeta_\rho\sin\theta_\zeta}{H} \frac{\partial \,\hat{f}_{(0)}}{\partial \chi}, \end{gather}$$

(3.13)$$\begin{gather}\,\hat{f}_{(1)} = \left( \hat{\sigma}_{a(1)} + 2 u_w\hat{p}_{(0)} \zeta_\rho\sin\theta_\zeta \right) E, \quad \cos\theta_\zeta>0,\enspace y=0, \end{gather}$$

(3.14)$$\begin{gather}\,\hat{f}_{(1)} = \hat{\sigma}_{b(1)} E, \quad \cos\theta_\zeta<0,\enspace y=1, \end{gather}$$

(3.15)\begin{gather} \left.\begin{gathered} \hat{\sigma}_{a(1)}={-}2\sqrt{\rm \pi} \iint\!\!\!\int_{\cos\theta_\zeta<0} \zeta_\rho^2\cos\theta_\zeta \kern0.06em\hat{f}_{(1)} \,\text{d}\zeta_\rho \,\text{d}\theta_\zeta \,\text{d}\zeta_z, \quad y=0, \\ \hat{\sigma}_{b(1)}= 2\sqrt{\rm \pi} \iint\!\!\!\int_{\cos\theta_\zeta>0} \zeta_\rho^2\cos\theta_\zeta \kern0.06em\hat{f}_{(1)} \,\text{d}\zeta_\rho \,\text{d}\theta_\zeta \,\text{d}\zeta_z, \quad y=1, \end{gathered}\right\} \end{gather}

(3.16)\begin{gather} \int_0^{2{\rm \pi}}\text{d}\chi \int_{0}^{1}\text{d} y\, H^2\int\!\!\! \int\!\!\! \int \zeta_\rho \kern0.06em\hat{f}_{(1)} \,\text{d}\zeta_\rho \,\text{d}\theta_\zeta \,\text{d}\zeta_z = \frac{\rm \pi}{\gamma}.\end{gather}

To analyse this, we introduce an approximation: the operator $\mathcal {D}_{ec}$ in (3.12) is simplified to

(3.17)\begin{equation} \mathcal{D}_{ec}'= \frac{\cos\theta_\zeta}{\gamma H}\frac{\partial}{\partial y} -c\frac{\sinh\eta \sin\theta_\zeta}{\sinh\eta_a} \frac{\partial}{\partial \theta_\zeta}, \end{equation}

omitting the term $\sin \chi \cos \theta _\zeta$ in $G$. This approximation may be permissible because the curvature term is crucial for the molecular velocities nearly tangential to the inner cylinder, i.e. around $\theta _\zeta =\pm {\rm \pi}/2$ (see figure 2a), at which the omitted term $\sin \chi \cos \theta _\zeta$ vanishes. As we will see in § 5, this approximation is sufficient for the purpose of this paper. Owing to this approximation, the operator $\mathcal {D}_{ec}^\prime$ preserves the parity with respect to $\theta _\zeta$. As a result, we can decompose the solution $\hat {f}_{(1)}$ into a sum of even and odd functions with respect to $\theta _\zeta$ as $\hat {f}_{(1)}=\hat {f}_{(1)}^{even}+\hat {f}_{(1)}^{odd}$. The even function $\hat {f}_{(1)}^{even}$ is a solution of the homogeneous Boltzmann equation that is responsible for $\hat {\sigma }_{a(1)}, \hat {\sigma }_{b(1)}$ and the subsidiary condition (3.16). A solution is a Maxwellian at rest

(3.18)\begin{equation} \,\hat{f}_{(1)}^{even} = C_{(1)} E, \end{equation}

where $C_{(1)}$ is an arbitrary function of $\chi$ subject to (3.16). The odd function $\hat {f}_{(1)}^{odd}$ is the particular solution that is responsible for the inhomogeneous terms. By putting $\hat {f}_{(1)}^{odd}=\hat {f}_{(0)} \phi$, the problem for $\hat {f}_{(1)}^{odd}$ can be reduced to a simpler problem for $\phi$

(3.19)$$\begin{gather} \zeta_\rho\mathcal{D}_{ec}' \phi = \frac{\hat{p}_{(0)}}{k} \mathcal{L}(\phi) -\frac{\zeta_\rho\sin\theta_\zeta}{H} \frac{1}{\hat{p}_{(0)}} \frac{\text{d} \hat{p}_{(0)}}{\text{d} \chi}, \end{gather}$$

(3.20)$$\begin{gather}\phi = 2 u_w \zeta_\rho\sin\theta_\zeta, \quad \cos\theta_\zeta>0,\enspace y=0, \end{gather}$$

(3.21)$$\begin{gather}\phi = 0, \quad \cos\theta_\zeta<0,\enspace y=1, \end{gather}$$

where $\mathcal {L}({\cdot })$ is the linearized collision operator defined by $E\mathcal {L}(\phi )=2\hat {J}(E,E\phi )$. Because of the linearity, the solution is given by

(3.22)\begin{equation} \phi(y, \chi, \boldsymbol{\zeta}) = \frac{1}{\hat{p}_{(0)}} \frac{\text{d} \hat{p}_{(0)}}{\text{d} \chi} \varPhi_{Pec}\left(y, \boldsymbol{\zeta}; \frac{k}{\hat{p}_{(0)}}, \chi \right) +u_w \varPhi_{Cec}\left(y, \boldsymbol{\zeta}; \frac{k}{\hat{p}_{(0)}}, \chi \right), \end{equation}

where $\boldsymbol {\zeta }$ is an abbreviation for $(\zeta _\rho, \theta _\zeta, \zeta _z)$. The functions $\varPhi _{Pec}(y, \boldsymbol {\zeta }; \tilde {k}, \chi )$ and $\varPhi _{Cec}(y, \boldsymbol {\zeta }; \tilde {k}, \chi )$ are defined by (A1) and (A2) and (A3)–(A5), respectively, in Appendix A; they depend on $c$ and $\varepsilon$ through the operator $\mathcal {D}_{ec}^\prime$. The parameter $\tilde {k}$ stands for $k/\hat {p}_{(0)}$, which may be termed a local Knudsen number due to the variation of the pressure $\hat {p}_{(0)}$.

Substituting (3.10), (3.18) and (3.22) into (3.1), the solution up to $\hat {f}=\hat {f}_{(0)} +\hat {f}_{(1)} c$ is written as

(3.23)\begin{align} & \hat{f}(y, \chi, \boldsymbol{\zeta}) = \hat{p}_{(0)} E \nonumber\\ &\quad \times \left\{1 +c\left[\frac{C_{(1)}}{\hat{p}_{(0)}} +\frac{1}{\hat{p}_{(0)}} \frac{\text{d} \hat{p}_{(0)}}{\text{d} \chi} \varPhi_{Pec}\left(y, \boldsymbol{\zeta}; \frac{k}{\hat{p}_{(0)}}, \chi \right) +u_w \varPhi_{Cec}\left(y, \boldsymbol{\zeta}; \frac{k}{\hat{p}_{(0)}}, \chi \right)\right]\right\}, \end{align}

in terms of the undetermined functions $\hat {p}_{(0)}$ and $C_{(1)}$.

It may be noted that there are more several advantages of the approximation (3.17). In addition to the solution $\phi$ being odd in $\theta _\zeta$, it is also symmetric with respect to $\chi ={\rm \pi}$. Further, the characteristic equation $\gamma H\textrm {d} y/\cos \theta _\zeta = -\sinh \eta _a \textrm {d}\theta _\zeta /(c\sinh \eta \sin \theta _\zeta )$ of (3.19), or written explicitly in the original variables $\eta$ as

(3.24)\begin{equation} \frac{\text{d}\eta}{(\cosh\eta-\cos\chi)\cos\theta_\zeta} =\frac{\text{d}\theta_\zeta}{\sinh\eta \sin\theta_\zeta}, \end{equation}

can be solved analytically to yield

(3.25)\begin{equation} \frac{\sin\theta_\zeta}{\cosh\eta-\cos\chi}=\text{const}. \end{equation}

These properties are convenient for an accurate numerical analysis of the boundary-value problems (A1) and (A2) and (A3)–(A5) of the two-dimensional Boltzmann equation to obtain $\varPhi _{Pec}$ and $\varPhi _{Cec}$.

3.3. Lubrication equation

Our next task is to determine the unknown function $\hat {p}_{(0)}$, and this is accomplished by using the mass conservation law. Substituting (3.23) into (2.31c) and then into (2.32), we obtain from the first-order mass conservation

(3.26)\begin{equation} \frac{\text{d}}{\text{d}\chi}\left[m_{Pec}\left(\frac{k}{\hat{p}_{(0)}}, \chi \right) \frac{\text{d} \hat{p}_{(0)}}{\text{d}\chi} +u_w\hat{p}_{(0)}m_{Cec}\left(\frac{k}{\hat{p}_{(0)}}, \chi \right)\right]=0, \end{equation}

where the functions $m_{Pec}(\tilde {k}, \chi )$ and $m_{Cec}(\tilde {k}, \chi )$, which depend on $c$ and $\varepsilon$, are defined by (A9) in Appendix A. As we are about to see, (3.26) plays a role of determining the leading-order pressure $\hat {p}_{(0)}$.

Suppose that the boundary-value problem (A1) and (A2) for $\varPhi _{Pec}$ and that (A3)–(A5) for $\varPhi _{Cec}$ are solved over a wide range of the parameters $\tilde {k}, \chi, c$ and $\varepsilon$, and that the database of the functions $m_{Pec}(\tilde {k}, \chi )$ and $m_{Cec}(\tilde {k}, \chi )$ is known. Then, (3.26), (3.9) and the periodic condition constitute the ordinary differential equation to determine $\hat {p}_{(0)}$. Once $\hat {p}_{(0)}$ is known, the velocity distribution function is given by (3.23). Substituting (3.23) into (2.31a)–(2.31g), the macroscopic variables are obtained. For example, the component $\hat {v}_\chi$ of the flow velocity, those of the stress tensor and the pressure $\hat {p}$ up to the non-trivial leading orders are given by

(3.27)$$\begin{gather} \hat{v}_{\chi}= c\left[\frac{1}{\hat{p}_{(0)}} \frac{\text{d} \hat{p}_{(0)}}{\text{d}\chi} u_{Pec}\left(y; \frac{k}{\hat{p}_{(0)}}, \chi \right) +u_w u_{Cec}\left(y; \frac{k}{\hat{p}_{(0)}}, \chi \right)\right], \end{gather}$$

(3.28)$$\begin{gather}\hat{p}_{\eta\eta}=\hat{p}=\hat{p}_{(0)}, \end{gather}$$

(3.29)$$\begin{gather}\hat{p}_{\chi\eta}= c\left[ \frac{\text{d} \hat{p}_{(0)}}{\text{d}\chi} S_{Pec}\left(y; \frac{k}{\hat{p}_{(0)}}, \chi \right) +u_w\hat{p}_{(0)} S_{Cec}\left(y; \frac{k}{\hat{p}_{(0)}}, \chi \right) \right], \end{gather}$$

where the functions $u_{Pec}(y; \tilde {k}, \chi )$ and $u_{Cec}(y; \tilde {k}, \chi )$ are defined by (A7), and the functions $S_{Pec}(y; \tilde {k}, \chi )$ and $S_{Cec}(y; \tilde {k}, \chi )$ are defined by (A8). Substituting (3.28) and (3.29) into (2.18) and (2.19), the eccentric force and the torque are obtained. Thus, (3.26) plays the role of determining the pressure distribution $\hat {p}_{(0)}$. In this sense, (3.26) may be called a generalized Reynolds equation.

The function $C_{(1)}$ is as yet undetermined. So, unlike the coaxial case (Doi Reference Doi2022), the truncation error of the solution at this stage is still $O(c)$. To determine $C_{(1)}$, the next-order analysis is necessary, which is briefly touched on in Appendix B. Instead of conducting the precise analysis, however, it is proposed in Appendix B to solve (3.26) subject to the modified subsidiary condition

(3.30)\begin{equation} \int_0^{2{\rm \pi}} \text{d}\chi \int_{0}^{1}\text{d} y\, H^2 \hat{p}_{(0)} = \frac{2{\rm \pi}}{\gamma} \left(1+\frac{c}{2}\right) ,\end{equation}

in place of (3.8). Provided that the nonlinear collision integral $\hat {J}(\,\hat {f}_{(1)},\hat {f}_{(1)})$ in the second-order analysis is negligibly small, this solution $\hat {p}_{(0)}$ yields $\hat {p}$ and the normal stress $\hat {p}_{\eta \eta }$ approximately up to the first order in $c$. Incidentally, when the Mach number based on the lubrication motion is not small in contrast to (2.1b), the difference between the normal stress and the pressure is non-negligible (Ansumali et al. Reference Ansumali, Karlin, Arcidiacono, Abbas and Prasianakis2007).

In the derivation of (3.26), we implicitly assumed that the Knudsen number $k$ is of $O(1)$. By a similar analysis to that in Doi (Reference Doi2022), we can show that the Reynolds equation for $k=c^{-n} (n=1, 2, \ldots )$ is given by (3.26) in which the functions $m_{Pec}(\tilde {k}, \chi )$ and $m_{Cec}(\tilde {k}, \chi )$ are replaced by $m_{Pec}(\infty, \chi )$ and $m_{Cec}(\infty, \chi )$, respectively. Thus, we find that (3.26) holds up to $k=\infty$ by making $n\to \infty$. Incidentally, the lubrication model (3.26) reduces to that for a coaxial annulus derived in Doi (Reference Doi2022) in the limit $\varepsilon \to 0$ keeping $c$ constant. Details are given in Appendix C.

3.4. Flow-rate coefficients

Equation (3.26) is similar to the conventional Reynolds equation for a one-dimensional and time-independent state, but there are two differences. First, the coefficients of the mass flow rates of Poiseuille and Couette flows in the latter are replaced by the functions $m_{Pec}(\tilde {k}, \chi )$ and $m_{Cec}(\tilde {k}, \chi )$. That is, the non-continuum effect is condensed in these functions; it is characterized by the first argument $\tilde {k}=k/\hat {p}_{(0)}$. These are determined by the solutions of flow problems of a rarefied gas as follows. The first function $m_{Pec}$ is determined by the solution $\varPhi _{Pec}$ of a flow induced by a pressure gradient imposed along a curved channel. The second function $m_{Cec}$ is determined by the solution $\varPhi _{Cec}$ of a flow along a curved channel induced by a tangential motion of one of the walls. In this sense, the functions $m_{Pec}$ and $m_{Cec}$ may be called the flow-rate coefficients of generalized Poiseuille and Couette flows. Second, the gas-film thickness is absent; it is incorporated into the functions $m_{Pec}$ and $m_{Cec}$. Because the generalized Poiseuille and Couette flows cannot be solved analytically unlike the Navier–Stokes system, we cannot establish an explicit expression of the coefficients in terms of the gas-film thickness. The variation of the gas-film thickness along the channel is characterized by the second argument $\chi$.

Some examples of the flow-rate coefficients are presented in figure 3 for the BGKW kinetic model. Figures 3(a) and 3(b) show, respectively, $-m_{Pec}$ and $m_{Cec}$ as functions of $\tilde {k}$ and $\chi$ for $\varepsilon =0.1$ and 0.9 with $c=0.05$. These functions are symmetric with respect to $\chi ={\rm \pi}$, and thus only $0\le \chi \le {\rm \pi}$ is shown. When the eccentricity $\varepsilon$ is vanishingly small, the flow is axially symmetric and these functions are thus independent of the longitudinal coordinate $\chi$. The results for $\varepsilon =0.1$ assume this tendency. The function $-m_{Pec}$ of generalized Poiseuille flow shows a slight Knudsen minimum about $\tilde {k}=1$. As the eccentricity $\varepsilon$ approaches unity, both flow rates shrink around $\chi ={\rm \pi}$ at which the channel is narrowest. A simple database of the functions $m_{Pec}$ and $m_{Cec}$ is given in Appendix D. The numerical data necessary for this database are provided by the author via Doi (Reference Doi2023) for wide ranges of the parameters $c$ and $\varepsilon$.

Figure 3. Flow-rate coefficients $m_{Pec}$ and $m_{Cec}$ for $\varepsilon =0.1$ and 0.9 ($c=0.05$) as functions of $\tilde {k}$ and $\chi$ (BGKW model); (a) $-m_{Pec}$ and (b) $m_{Cec}$. Dotted line for $\varepsilon =0.1$ and solid line for $\varepsilon =0.9$. These functions are symmetric with respect to $\chi ={\rm \pi}$.

3.5. Lubrication equation without the curvature term

Let us now look back to § 3.1 and discuss what happens if we conduct the perturbation (3.1) by treating the curvature term of (2.23) as a higher-order term. The analysis is quite similar to that in §§ 3.2 and 3.3, and thus only the final result is presented here, leaving the derivation to Appendix E. The lubrication equation thus obtained is

(3.31)\begin{equation} \frac{\text{d}}{\text{d}\chi}\left[m_{Pwoc}\left(\frac{k}{\hat{p}_{(0)}}, \chi\right) \frac{\text{d} \hat{p}_{(0)}}{\text{d}\chi}+u_w\hat{p}_{(0)} m_{Cwoc} \left(\frac{k}{\hat{p}_{(0)}}, \chi \right)\right]=0. \end{equation}

Equation (3.31) is of the same form as (3.26); the only difference is that the functions $m_{Pec}$ and $m_{Cec}$ are replaced, respectively, by $m_{Pwoc}$ and $m_{Cwoc}$ defined by (E10). For discrimination, let us call (3.31) the lubrication model without the curvature term, or the WOC model for short. In contrast, let us call (3.26) the improved model. One of our major objectives is to demonstrate that the solution of the WOC model produces an error of $O(c^{1/2})$ when the Knudsen number is large.

We have now derived two lubrication models, namely, improved model (3.26) and the WOC model (3.31). Our remaining task is to assess whether the solutions of these models approximate that of the Boltzmann equation. For this assessment, accurate solution of the Boltzmann equation is required as a reference. This solution is provided in § 4. The remainder of this paper is devoted to this assessment.

4.1. Preliminaries

In this section, a direct numerical analysis of the boundary-value problem (2.23)–(2.30) is conducted. In this numerical analysis, we assume that the gas is governed by the BGKW kinetic equation. That is, the collision integral is given by

(4.1)\begin{equation} \left.\begin{gathered} \hat{J}(\,\hat{f}, \,\hat{f})= \hat{\rho}( \,\hat{f}_e -\,\hat{f} ), \\ \,\hat{f}_e= \frac{\hat{\rho}}{({\rm \pi}\hat{T})^{3/2}} \exp \left(-\frac{ (\zeta_\rho\cos\theta_\zeta-\hat{v}_\eta)^2 + (\zeta_\rho\sin\theta_\zeta-\hat{v}_\chi)^2 +\zeta_z^2}{\hat{T}}\right), \end{gathered}\right\} \end{equation}

where $\hat {\rho }, \hat {v}_\eta, \hat {v}_\chi$ and $\hat {T}$ are given by (2.31a)–(2.31d). The mean free path $\ell$ of the BGKW model is related to the viscosity $\mu$ of the gas by (Sone Reference Sone2007)

(4.2)\begin{equation} \mu= \frac{\sqrt{\rm \pi}}{2} \frac{p_0}{(2RT_0)^{1/2}} \ell. \end{equation}

Note that the approximated operator (3.17) is never used in this direct numerical analysis.

4.2. Numerical method

The method of numerical analysis adopted here is based on that in Doi (Reference Doi2019). The common part is thus outlined here only briefly. First, the following marginal distribution functions are introduced (Chu Reference Chu1965):

(4.3a,b)\begin{equation} g_1= \int_{-\infty}^{\infty} \,\hat{f}\, \text{d}\zeta_z, \quad g_2= 2\int_{-\infty}^{\infty} \zeta_z^2 \,\hat{f}\, \text{d}\zeta_z. \end{equation}

Multiplying both sides of (2.23)–(2.29) by $1$ or $2\zeta _z^2$ and integrating over $-\infty <\zeta _z<\infty$, we obtain a reduced boundary-value problem for $g_1$ and $g_2$ in the four-dimensional space $y, \chi, \zeta _\rho$ and $\theta _\zeta$, i.e. the fifth variable $\zeta _z$ is eliminated. Second, the semi infinite range $0\le \zeta _\rho <\infty$ is replaced by a finite range $0\le \zeta _\rho \le \zeta _D$, where $\zeta _D$ is a constant such that the distribution functions $g_1$ and $g_2$ are sufficiently small around $\zeta _\rho =\zeta _D$. Third, rectangular mesh points are arranged in the finite four-dimensional domain $0\le y \le 1$, $0\le \chi \le 2{\rm \pi}, 0\le \zeta _\rho \le \zeta _D$ and $-{\rm \pi} \le \theta _\zeta \le {\rm \pi}$. Then, the boundary-value problem (2.23)–(2.30) is discretized and numerically solved using a finite-difference method. One of the features of the present problem is that the Boltzmann equation is written in a bipolar coordinate system, from which the following difficulties arise.

Because the gas region is over the convex inner cylinder, the distribution functions $g_1$ and $g_2$ are discontinuous in the $\theta _\zeta$–$\chi$–$y$ phase space (Sone Reference Sone2007). Figure 4(a) shows a schematic of a cross-section $\chi =\textrm {const}$ of it. (We discuss only $\theta _\zeta >0$ side for simplicity; the other side $\theta _\zeta <0$ is similar.) The solid lines in figure 4(a) represent the characteristics of the Boltzmann equation (2.23). The boundary condition (2.25) on the inner cylinder $y=0$ is applied only in $\theta _\zeta <{\rm \pi} /2$, and thus the distribution function is discontinuous at $y=0$ and $\theta _\zeta ={\rm \pi} /2$. This discontinuity propagates along the characteristics

(4.4)\begin{equation} \frac{\text{d} y}{(\gamma H)^{{-}1}\cos\theta_\zeta}=\frac{\text{d} \theta_\zeta}{-c G} =\frac{\text{d} \chi}{c H^{{-}1}\sin\theta_\zeta}\end{equation}

of the Boltzmann equation (2.23), to form the surface of discontinuity. An example is shown in figure 4(b). A numerical method to avoid the finite difference across the discontinuous surface has been developed for cylindrical coordinates in Sugimoto & Sone (Reference Sugimoto and Sone1992). A feature of the bipolar coordinates in the present case is that the surface of discontinuity depends on $\chi$ coordinate, cf. figure 4(b). Because of this, it is too complicated to establish a direct extension of the method of Sugimoto & Sone (Reference Sugimoto and Sone1992). We therefore use the following method, which is an application of Sone & Sugimoto (Reference Sone and Sugimoto1995). Let a division of regions I, II and III be made as shown in figure 4(a), where region II contains the discontinuous curve. First, in region I, the Boltzmann equation is solved from the boundary condition at $y=1$ using the standard finite-difference method. The distribution function on the plane $\theta _\zeta ={\rm \pi} /2$ is obtained. Second, in region II, the distribution function at an arbitrary point, say A, is solved as follows. The characteristic (4.4) is traced back to reach a boundary point, say B, of region II. If B lies on $y=0$, then the distribution function there is known from the boundary condition. From the data at B, we numerically integrate the Boltzmann equation from B to A along the characteristic. Finally, in region III, the Boltzmann equation is solved from the boundary condition at $y=0$ using a finite difference with the aid of the data in region II. To calculate macroscopic variables at a given physical coordinates $(y,\chi )$, the value of $\theta _\zeta$ (position C) on the discontinuous curve in figure 4(a) is required. It is determined by seeking the characteristic (4.4) that starts from some point on the line $(y,\theta _\zeta )=(0,{\rm \pi} /2)$ and passes the horizontal line possessing the desired $(y,\chi )$ using a shooting method. The distribution function at C is obtained in a similar way to that in region II. A shortcoming of this method is that a large amount of computational time is required in region II.

Figure 4. Discontinuity in the velocity distribution function and the numerical method. (a) Schematic view of a cross-section $\chi =\textrm {const}$ in the $\theta _\zeta -\chi -y$ phase space. (b) Characteristics (4.4) starting from the line $y=0$ and $\theta _\zeta ={\rm \pi} /2$, which form the surface of discontinuity ($c=0.05, \varepsilon =0.9$). In (a), the thick lines represent the intervals along which the boundary conditions on the cylinders are imposed. The double lines in $\theta _\zeta <{\rm \pi} /2$ represent the section of the discontinuous surface in (b). The solid lines with arrows represent the characteristics of the Boltzmann equation along which the finite-difference computation should proceed. The Boltzmann equation (2.23) is solved using the finite-difference method in regions I and III, whereas it is integrated along the characteristics in region II.

Regarding the second difficulty, another feature of the bipolar coordinates in the present case is that $G$ in (4.4) changes sign across the surfaces

(4.5)\begin{equation} \tan\theta_\zeta= \frac{\sin\chi}{\sinh\eta(y)}. \end{equation}

The lines in a cross-section $\chi =\textrm {const}$ are schematically shown in dashed lines in figure 5. Because $\textrm {d}\theta _\zeta$ of (4.4) changes sign across these dashed lines, the characteristics of the Boltzmann equation are those as shown in solid lines with arrows. The finite-difference method should follow these directions, or it will diverge. Because the separation lines (4.5) are not vertical, a precise numerical analysis is difficult. We therefore use an approximation. When $c$ is small, the separation lines (4.5) are close to vertical. Thus, they may be approximated by the nearest vertical lines along which the mesh points align. For the dashed line in ${\rm \pi} /2<\theta _\zeta <{\rm \pi}$ for example, the Boltzmann equation is first solved from $y=1$ for the mesh points along this vertical line by the finite-difference method imposing $G=0$. Once the solution on this line is known, the finite difference can be developed in the left and right directions from this line. A similar process is adopted to the other dashed line.

Figure 5. Schematic view of the cross-section $\chi =\textrm {const}$ of the $\theta _\zeta -\chi -y$ phase space (cf. figure 4a). The dashed lines represent the separation lines (4.5) across which the sign of $\textrm {d}\theta _\zeta$ of the characteristics (4.4) changes. The solid lines with arrows represent a schematic of the characteristics of the Boltzmann equation along which the finite-difference computation should proceed.

In this way, a finite-difference approach to the Boltzmann equation in a bipolar coordinate system is accompanied by particular difficulties. Nevertheless, we use the finite-difference method rather than the direct-simulation Monte Carlo (DSMC) method. This is because the purpose of this direct numerical analysis is to present accurate reference data for the assessment of the lubrication models in § 3 when both $c$ and the flow speed $\hat {v}_w$ are small. In this situation, a close examination, especially that in the last figure of this paper, would be hopeless if using the stochastic methods such as the DSMC method.

4.3. Computational conditions and accuracy tests

In this paper, the computations are conducted only for the cases of $\hat {v}_w(=c u_w)=0.1$.

The computational conditions are as follows. For the $y$ coordinate, the $N_y+1$ mesh points are arranged non-uniformly in the interval $0\le y\le 1$, where $N_y=100$. The mesh size is a minimum of 0.0021 at $y=0$ and $y=1$, and it is uniform and a maximum of 0.0125 in the interval $0.1 \le y \le 0.9$. For $\chi$, $N_x+1$ mesh points are arranged uniformly in the interval $0\le \chi \le 2{\rm \pi}$, where $N_x=200$. For $\zeta _\rho$, $N_u+1$ mesh points are arranged uniformly in the interval $0\le \zeta _\rho \le \zeta _D$, where $N_u=32$ and $\zeta _D=5$. For $\theta _\zeta$, $N_v+1$ mesh points are arranged uniformly in the interval $-{\rm \pi} \le \theta _\zeta \le {\rm \pi}$, where $N_v=400$.

The results of accuracy tests are as follows.

(i) Conservation law. According to (2.32), the dimensionless mass flow rate $\int _0^1 H \hat {\rho }\hat {v}_\chi \,\textrm {d} y$ is theoretically independent of $\chi$. Thus, uniformness of this quantity serves for a measure of the accuracy. The variation of the mass flow rate of the present computation over $0\le \chi \le 2{\rm \pi}$ is less than 0.52 %.

(ii) Dependence of the mesh system. For a test of accuracy, we conducted re-computations using coarser mesh systems in addition to the production run P with $(N_y,N_x,N_u,N_v)=(100,200,32,400)$, namely, the coarser system A with $(N_y,N_x,N_u,N_v)=(50,100,32,200)$ and the coarsest system B with $(N_y,N_x,N_u,N_v)=(24,50,32,100)$. By examining the differences between the three runs, i.e. B–P and A–P, the error in the production run P is estimated. From this test, it is estimated that the numerical error in the dimensionless pressure $\hat {p}$ over $0\le \chi \le 2{\rm \pi}$ at $y=0$ is less than 0.38 %, and that the numerical error in the flow velocity $\hat {v}_{\chi }$ over $0\le y \le 1$ at the cross-section $\chi =0$ is less than 0.19 %. Further, the numerical errors in the eccentric force $(F_1, F_2)$ in (2.18) and the torque $N$ in (2.19) are estimated to be less than 0.26 %; in particular for $\varepsilon =0.5$, the error is less than 0.14 %.