Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-29T17:19:15.724Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized phase average with applications to sensor-based flow estimation of the wall-mounted square cylinder wake

Published online by Cambridge University Press:  06 November 2013

J. A. Bourgeois ,
B. R. Noack  and
R. J. Martinuzzi
J. A. Bourgeois
Affiliation:
Department of Mechanical and Manufacturing Engineering, Schulich School of Engineering, University of Calgary, 2500 University Drive NW, Calgary, AB, T2N 1N4, Canada
B. R. Noack
Affiliation:
Institut PPRIME, CNRS - Université de Poitiers - ENSMA, UPR 3346, Département Fluides, Thermique, Combustion, CEAT, 43 rue de l’Aérodrome, F-86036 POITIERS CEDEX, France
R. J. Martinuzzi*
Affiliation:
Department of Mechanical and Manufacturing Engineering, Schulich School of Engineering, University of Calgary, 2500 University Drive NW, Calgary, AB, T2N 1N4, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

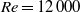We experimentally investigate the three-dimensional wake behind a finite wall-mounted square cylinder at $\mathit{Re}= 12\hspace{0.167em} 000$ and aspect ratio of 4. Focus is placed on the base flow and oscillatory fluctuation. Time-resolved three-dimensional velocity fields are constructed from high-frame-rate particle image velocimetry (PIV) and simultaneously recorded surface pressure measurements. All three velocity components are resolved in a rectangular near-wake region by two orthogonal dense arrays of parallel PIV planes. A key enabler is a generalized phase average incorporating a slowly varying base flow, a variable oscillation amplitude and higher harmonics. These generalizations reduce the instantaneous residual 30 % below those of a traditional phase average. Moreover, the resolved variations reveal analytical constraints of the mean flow and oscillation levels, such as the mean-field paraboloid. The proposed methodology for generalized phase averaging and for construction of three-dimensional velocity fields from two-dimensional PIV data is applicable to a large class of turbulent flows with oscillatory dynamics.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Wakes/Jets: Jets Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 736 , 10 December 2013 , pp. 316 - 350
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.Google Scholar
Bonnet, J.-P. (Ed.) 1998 Eddy Structure Identification. CISM Courses and Lectures, vol. 353. Springer.Google Scholar
Borée, J. 2003 Extended proper orthogonal decomposition: a tool to analyse correlated events in turbulent flows. Exp. Fluids 35, 188–192.CrossRefGoogle Scholar
Bourgeois, J. A., Sattari, P. & Martinuzzi, R. J. 2011 Alternating half-loop shedding in the turbulent wake of a finite surface-mounted square cylinder with a thin boundary layer. Phys. Fluids 23, 095101.Google Scholar
Deane, A. E., Kevrekidis, I. G., Karniadakis, G. E. & Orszag, S. A. 1991 Low-dimensional models for complex geometry flows: application to grooved channels and circular cylinders. Phys. Fluids A 3, 2337–2354.CrossRefGoogle Scholar
Dušek, J., Le Gal, P. & Fraunié, P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.CrossRefGoogle Scholar
Farge, M., Schneider, K., Pellegrino, G., Wray, A. & Rogallo, B. 2003 Coherent vortex extraction in three-dimensional homogeneous turbulence: comparison between CVS–wavelet and POD–Fourier decompositions. Phys. Fluids 15, 2886–2896.Google Scholar
Fletcher, C. A. J. 1984 Computational Galerkin Methods, 1st edn. Springer.Google Scholar
Glauser, M., Eaton, E., Taylor, J., Cole, D., Ukeiley, L., Citrini, J. H., George, W. K. & Stokes, S. 1999 Low-dimensional descriptions of turbulent flow: experiment and modelling. In AIAA Fluids 1999 Conference and Exhibit. Norfolk, VA, USA, June 28–July 1, 1999, AIAA paper 99-3699.Google Scholar
Haller, G. 2001 Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D 149, 248–277.CrossRefGoogle Scholar
Haller, G. 2005 An objective definition of a vortex. J. Fluid Mech. 525, 1–26.Google Scholar
Holmes, P., Lumley, J. L., Berkooz, G. & Rowley, C. W. 2012 Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research.Google Scholar
Kasten, J., Hotz, I., Noack, B. R. & Hege, H.-C. 2012a Vortex merge graphs in two-dimensional unsteady flow fields. In Proceedings of the Joint EG/IEEE Symposium on Visualization (EuroVis 2012).Google Scholar
Kasten, J., Reininghaus, J., Hotz, I., Hege, H.-C., Noack, B. R., Daviller, G., Comte, P. & Morzynśki, M. 2012b Acceleration feature points of unsteady shear flows. SIAM J. Appl. Dyn. Syst. (submitted).Google Scholar
Liu, J. T. C. 1989 Coherent structures in transitional and turbulent free shear flows. Annu. Rev. Fluid Mech. 21, 285–315.CrossRefGoogle Scholar
Luchtenburg, D. M., Günter, B., Noack, B. R., King, R. & Tadmor, G. 2009 A generalized mean-field model of the natural and actuated flows around a high-lift configuration. J. Fluid Mech. 623, 283–316.Google Scholar
Lugt, H. J. 1995 Vortex Flow in Nature and Technology, reprint edn. Krieger Publishing Company.Google Scholar
Noack, B. R. 2006 Niederdimensionale Galerkin–Modelle für laminare und transitionelle freie Scherströmungen (translation: low-dimensional Galerkin models of laminar and transitional free shear flows). Habilitation thesis, Berlin Institute of Technology, Germany.Google Scholar
Noack, B. R., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.Google Scholar
Noack, B. R., Morzyński, M. & Tadmor, G. (Eds) 2011 Reduced-Order Modelling for Flow Control. CISM Courses and Lectures, vol. 528. Springer.CrossRefGoogle Scholar
Noack, B. R., Papas, P. & Monkewitz, P. A. 2005 The need for a pressure-term representation in empirical Galerkin models of incompressible shear flows. J. Fluid Mech. 523, 339–365.Google Scholar
Noack, B. R., Schlegel, M., Morzyński, M. & Tadmor, G. 2010 System reduction strategy for Galerkin models of fluid flows. Intl J. Numer. Meth. Fluids 63 (2), 231–248.Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H.-C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.Google Scholar
Perrin, R., Braza, M., Cid, E., Cazin, S., Moradei, F., Barthet, A., Sevrain, A. & Hoarau, Y. 2006 Near-wake turbulence properties in the high Reynolds number incompressible flow around a circular cylinder measured by two- and three-component PIV. Flow Turbul. Combust. 77, 185–204.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19, 125–155.Google Scholar
Press, W. H., Flannery, B. P., Teukolsky, S. A. & Vetterling, W. T. 1986 Numerical Recipes. The Art of Scientific Computing. Cambridge University Press, Sec. 3.6, pp. 95–97.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54, 263–288.Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 645, 115–127.Google Scholar
Rowley, C. W. & Williams, D. R. 2006 Dynamics and control of high-Reynolds number flows over open cavities. Annu. Rev. Fluid Mech. 38, 251–276.Google Scholar
Sattari, P., Bourgeois, J. A. & Martinuzzi, R. J. 2012 On the vortex dynamics in the wake of a finite surface-mounted square cylinder. Exp. Fluids 52 (5), 1149–1167.Google Scholar
Schlegel, M., Noack, B. R., Jordan, P., Dillmann, A., Gröschel, E., Schröder, W., Wei, M., Freund, J. B., Lehmann, O. & Tadmor, G. 2012 On least-order flow representations for aerodynamics and aeroacoustics. J. Fluid Mech. 697, 367–398.CrossRefGoogle Scholar
Schmid, P. J. 2010 Dynamic mode decomposition for numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Tadmor, G., Lehmann, O., Noack, B. R., Cordier, L., Delville, J., Bonnet, J.-P. & Morzyński, M. 2011 Reduced-order models for closed-loop wake control. Phil. Trans. R. Soc. A 369, 1513–1524.Google Scholar
Tadmor, G., Lehmann, O., Noack, B. R. & Morzyński, M. 2010 Mean field representation of the natural and actuated cylinder wake. Phys. Fluids 22, 034102.Google Scholar
Taylor, J. A. & Glauser, M. N. 2004 Towards practical flow sensing and control via POD and LSE based low-dimensional tools. Trans. ASME: J. Fluids Engng 126, 337–345.Google Scholar
Wang, H. & Zhou, Y. 2009 The finite-length square cylinder near-wake. J. Fluid Mech. 638, 453–490.Google Scholar
Wang, H., Zhou, Y., Chan, C. K. & Lam, K. 2006 Effect of initial conditions on interaction between a boundary layer and a wall-mounted finite-length-cylinder wake. Phys. Fluids 18, 065106.Google Scholar
Westerweel, J. 2000 Theoretical analysis of the measurement precision in particle image velocimetry. Exp. Fluids 29, S3–S12.CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar