Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T06:53:22.577Z Has data issue: false hasContentIssue false
  • English
  • Français

The generalized Onsager model for the secondary flow in a high-speed rotating cylinder

Published online by Cambridge University Press:  26 September 2011

S. Pradhan  and
V. Kumaran
S. Pradhan
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
V. Kumaran*
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The generalizations of the Onsager model for the radial boundary layer and the Carrier–Maslen model for the end-cap axial boundary layer in a high-speed rotating cylinder are formulated for studying the secondary gas flow due to wall heating and due to insertion of mass, momentum and energy into the cylinder. The generalizations have wider applicability than the original Onsager and Carrier–Maslen models, because they are not restricted to the limit 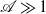, though they are restricted to the limit 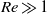and a high-aspect-ratio cylinder whose length/diameter ratio is large. Here, the stratification parameter 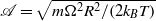. This parameter 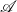is the ratio of the peripheral speed, 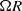, to the most probable molecular speed, 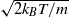, the Reynolds number 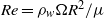, where 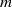is the molecular mass, 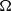and 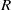are the rotational speed and radius of the cylinder, 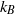is the Boltzmann constant, 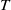is the gas temperature, 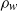is the gas density at wall, and 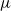is the gas viscosity. In the case of wall forcing, analytical solutions are obtained for the sixth-order generalized Onsager equations for the master potential, and for the fourth-order generalized Carrier–Maslen equation for the velocity potential. For the case of mass/momentum/energy insertion into the flow, the separation-of-variables procedure is used, and the appropriate homogeneous boundary conditions are specified so that the linear operators in the axial and radial directions are self-adjoint. The discrete eigenvalues and eigenfunctions of the linear operators (sixth-order and second-order in the radial and axial directions for the Onsager equation, and fourth-order and second-order in the axial and radial directions for the Carrier–Maslen equation) are determined. These solutions are compared with direct simulation Monte Carlo (DSMC) simulations. The comparison reveals that the boundary conditions in the simulations and analysis have to be matched with care. The commonly used ‘diffuse reflection’ boundary conditions at solid walls in DSMC simulations result in a non-zero slip velocity as well as a ‘temperature slip’ (gas temperature at the wall is different from wall temperature). These have to be incorporated in the analysis in order to make quantitative predictions. In the case of mass/momentum/energy sources within the flow, it is necessary to ensure that the homogeneous boundary conditions are accurately satisfied in the simulations. When these precautions are taken, there is excellent agreement between analysis and simulations, to within 10 %, even when the stratification parameter is as low as 0.707, the Reynolds number is as low as 100 and the aspect ratio (length/diameter) of the cylinder is as low as 2, and the secondary flow velocity is as high as 0.2 times the maximum base flow velocity. The predictions of the generalized models are also significantly better than those of the original Onsager and Carrier–Maslen models, which are restricted to thin boundary layers in the limit of high stratification parameter.

JFM classification

Compressible Flows: Gas dynamics Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 686 , 10 November 2011 , pp. 109 - 159
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Andrade, D. A. & Bastos, J. L. F. 1998 A gas centrifuge thermal hydrodynamical model. In The Proceedings of Sixth International Workshop on Separation Phenomena in Liquids and Gases, Nagoya, pp. 92–99.Google Scholar
2. Aoki, E. & Suzuki, M. 1985 Numerical studies on gas flow around scoop of a gas centrifuge. In The Proceedings of Sixth Workshop on Gases in Strong Rotation, Tokyo (ed. Takashima, Y. ). pp. 11–29.Google Scholar
3. Babarsky, R. J., Herbst, W. I. & Wood, H. G. 2002 A new variational approach to gas flow in a rotating system. Phys. Fluids 14 (10), 3624–3640.CrossRefGoogle Scholar
4. Babarsky, R. J. & Wood, H. G. 1990 Approximate eigensolutions for non-axisymmetric rotating compressible flows. Comput. Meth. Appl. Mech. Engng 81, 317–372.CrossRefGoogle Scholar
5. Bark, F. H. & Bark, T. H. 1976 On vertical boundary layers in a rapidly rotating gas. J. Fluid Mech. 78, 749–761.CrossRefGoogle Scholar
6. Berger, M. H. 1987 Finite element analysis of flow in a gas-filled rotating annulus. Intl J. Numer. Meth. Fluids 7, 215–231.CrossRefGoogle Scholar
7. Bird, G. A. 1963 Approach to translational equilibrium in a rigid sphere gas. Phys. Fluids 6, 1518–1519.CrossRefGoogle Scholar
8. Bird, G. A. 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Clarendon.CrossRefGoogle Scholar
9. Bourn, R., Peterson, T. D. & Wood, H. G. 1999 Solution of the pancake model for flow in a gas centrifuge by means of a temperature potential. Comput. Meth. Appl. Mech. Engng 178, 183–197.CrossRefGoogle Scholar
10. Brouwers, J. J. H. 1978 On compressible flow in a gas centrifuge and its effect on maximum separative power. Nucl. Technol. 39, 311–322.CrossRefGoogle Scholar
11. Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-Uniform Gases. Cambridge University Press.Google Scholar
12. Gunzburger, M. D. & Wood, H. G. 1982 A finite element method for the Onsager pancake equation. Comput. Meth. Appl. Mech. Engng 31, 43–59.CrossRefGoogle Scholar
13. Gunzburger, M. D., Wood, H. G. & Jordan, J. A. 1984 A finite element method for gas centrifuge problems. SIAM J. Sci. Stat. Comput. 5.CrossRefGoogle Scholar
14. Harada, I. 1980a A numerical study of weakly compressible rotating flows in a gas centrifuge. Nucl. Sci. Engng 73, 225–241.CrossRefGoogle Scholar
15. Harada, I. 1980b Computation of strongly compressible rotating flows. J. Comput. Phys. 38, 335–356.CrossRefGoogle Scholar
16. Hausman, M. A. & Roberts, W. W. 1984 Three dimensional stratified gas flows past an obstacle. J. Comput. Phys. 55, 347–368.CrossRefGoogle Scholar
17. Hittinger, M., Holt, M. & Soubbaramayer, B. 1981 Numerical solution of the flow field near a gas centrifuge scoop. In The Proceedings of Fourth Workshop on Gases in Strong Rotation, Oxford (ed. Ratz, E. ). pp. 22–40.Google Scholar
18. Hittinger, M., Holt, M., Soubbaramayer, B. & Cortet, C. 1983 Simulation of gas flow in front of the scoop of a gas centrifuge. In The Proceedings of Fifth Workshop on Gases in Strong Rotation, Charlottesville, Virginia (ed. Wood, H. G. ). pp. 515–532.Google Scholar
19. Jung, E. 1983 An analytic solution of the linearized flow equations using the method of eigenvalues. In The Proceedings of Fifth Workshop on Gases in Strong Rotation, Charlottesville, Virginia (ed. Wood, H. G. ). pp. 247–275.Google Scholar
20. Kai, T. 1983 Analysis of separation performance of gas centrifuge. In The Proceedings of Fifth Workshop on Gases in Strong Rotation, Charlottesville, Virginia (ed. Wood, H. G. ). pp. 1–42.Google Scholar
21. Matsuda, T. 1976 A New proposal of gas centrifuge with desirable counter-current. J. Nucl. Sci. Technol. 13, 98–99.CrossRefGoogle Scholar
22. Matsuda, T. & Hashimoto, K. 1978 The structure of the Stewartson layers in a gas centrifuge. Part 1. Insulated end plates. J. Fluid Mech. 85, 433–442.CrossRefGoogle Scholar
23. Matsuda, T. & Nakagawa, K. 1983 A new type of boundary layer in a rapidly rotating gas. J. Fluid Mech. 126, 431–442.CrossRefGoogle Scholar
24. Mikami, H. 1973 Thermally induced flow in a gas centrifuge. J. Nucl. Sci. Technol. 10, 580–583.CrossRefGoogle Scholar
25. Mikami, H. 1981 Rotating supersonic flow about scoop inlet using an unsteady implicit technique. In The Proceedings of Fourth Workshop on Gases in Strong Rotation, Oxford (ed. Ratz, E. ). pp. 94–112.Google Scholar
26. Mikami, H. 1985 Two dimensional numerical calculation of flow fields about scoop inlet by the piecewise linear method. In The Proceedings of Sixth Workshop on Gases in Strong Rotation, Tokyo (ed. Takashima, Y. ). pp. 67–85.Google Scholar
27. Nakayama, W. & Torii, T. 1974 Numerical analysis of separative power of isotope centrifuges. J. Nucl. Sci. Technol. 11, 495–504.CrossRefGoogle Scholar
28. Olander, D. R. 1981 The theory of uranium enrichment by the gas centrifuge. Prog. Nucl. Energy 8, 1–33.CrossRefGoogle Scholar
29. Ribando, R. J. 1984 A finite difference solution of Onsager’s model for flow in a gas centrifuge. Comput. Fluids 12 (3), 235–252.CrossRefGoogle Scholar
30. Roberts, W. W. 1985 Three dimensional stratified gas flows past impact probes and scoops: N-body Monte Carlo calculations. In The Proceedings of Sixth Workshop on Gases in Strong Rotation, Tokyo (ed. Takashima, Y. ). pp. 115–132.Google Scholar
31. Roberts, W. W. & Hausman, M. A. 1988 Hypersonic, stratified gas flows past an obstacle: Direct Simulation Monte Carlo calculations. J. Comput. Phys. 77, 283–317.CrossRefGoogle Scholar
32. Roblin, P. & Doneddu, F. 2000 Direct Monte-Carlo simulations in a gas centrifuge. In 22nd International Symposium on Rarefied Gas Dynamics (ed. Bartel, T. J. & Gallis, M. C. ). pp. 169–173. American Institute of Physics.Google Scholar
33. Sakurai, T. 1981 Linearized thin-wing theory of gas-centrifuge scoops. J. Fluid Mech. 103, 257–273.CrossRefGoogle Scholar
34. Viecelli, J. A. 1983 Exponential difference operator approximation for the sixth order Onsager equation. J. Comput. Phys. 50, 162–170.CrossRefGoogle Scholar
35. Villani, S. (ed) 1979 Uranium Enrichment. Springer.CrossRefGoogle Scholar
36. Volosciuk, K. 1981 Application of the vortex transport equations to the calculation of 2 and 3 dimensional extraction chamber flows. In The Proceedings of Fourth Workshop on Gases in Strong Rotation, Oxford (ed. Ratz, E. ). pp. 604–622.Google Scholar
37. Walz, A., Volosciuk, K. & Schutz, H. 1983 Numerical investigations of the flow field near a model of a scoop using the vortex transport equations. In The Proceedings of Fifth Workshop on Gases in Strong Rotation, Charlottesville, Virginia (ed. Wood, H. G. ). pp. 425–458.Google Scholar
38. Wood, H. G. & Babarsky, R. J. 1992 Analysis of a rapidly rotating gas in a pie-shaped cylinder. J. Fluid Mech. 239, 249–271.CrossRefGoogle Scholar
39. Wood, H. G., Jordan, J. A. & Gunzburger, M. D. 1984 The effect of curvature on the flow field in rapidly rotating gas centrifuges. J. Fluid Mech. 140, 373–395.CrossRefGoogle Scholar
40. Wood, H. G. & Morton, J. B. 1980 Onsager’s pancake approximation for the fluid dynamics of a gas centrifuge. J. Fluid Mech. 101, 1–31.CrossRefGoogle Scholar
41. Wood, H. G. & Sanders, G. 1983 Rotating compressible flows with internal sources and sinks. J. Fluid Mech. 127, 299–311.CrossRefGoogle Scholar