Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T23:05:04.630Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized logarithmic law for high-order moments in turbulent boundary layers

Published online by Cambridge University Press:  19 February 2013

Charles Meneveau  and
Ivan Marusic
Charles Meneveau
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

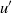High-Reynolds-number data in turbulent boundary layers are analysed to examine statistical moments of streamwise velocity fluctuations ${u}^{\prime } $. Prior work has shown that the variance of ${u}^{\prime } $ exhibits logarithmic behaviour with distance to the surface, within an inertial sublayer. Here we extend these observations to even-order moments. We show that the 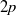$2p$-order moments, raised to the power 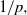$1/ p, $ also follow logarithmic behaviour according to 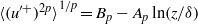$\langle \mathop{({u}^{\prime + } ){}^{2p} \rangle }\nolimits ^{1/ p} = {B}_{p} - {A}_{p} \ln (z/ \delta )$, where 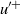${u}^{\prime + } $ is the velocity fluctuation normalized by the friction velocity, $\delta $ is an outer length scale and 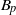${B}_{p} $ are non-universal constants. The slopes ${A}_{p} $ in the logarithmic region appear quite insensitive to Reynolds number, consistent with universal behaviour for wall-bounded flows. The slopes differ from predictions that assume Gaussian statistics, and instead are consistent with sub-Gaussian behaviour.

JFM classification

Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent boundary layers
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 719 , 25 March 2013 , R1
Copyright
©2013 Cambridge University Press

References

Alfredsson, P. H., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the ‘outer’ peak. Phys. Fluids 23, 041702.CrossRefGoogle Scholar
Fernholz, F. F. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32, 245–311.CrossRefGoogle Scholar
Hultmark, M. 2012 A theory for the streamwise turbulent fluctuations in high Reynolds number pipe flow. J. Fluid Mech. 707, 575–584.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 94501.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. P. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Jimenez, J. 1998 Turbulent velocity fluctuations need not be Gaussian. J. Fluid Mech. 376, 139–147.Google Scholar
Jimenez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
von Kármán, T. 1930 Mechanische Aehnlichkeit und Turbulenz. In Proceedings of Third International Congress for Applied Mechanics, vol. 1, pp. 79–93. Sveriges Lotografiska Tryckerier, Stockholm.Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Marusic, I. 2012 The logarithmic region of wall turbulence: universality, structure and interactions. In Proceedings of 18th Australasian Fluid Mechanics Conference, 3rd–7th December 2012 (ed. Brandner, P. A. & Pearce, B. W.). Australasian Fluid Mechanics Society.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15, 2461–2464.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Ng, H. C. H., Monty, J. P., Hutchins, N., Chong, M. S. & Marusic, I. 2011 Comparison of turbulent channel and pipe flows with varying Reynolds numbers. Exp. Fluids 51, 1261–1281.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. M. & Chong, M. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Prandtl, L. 1925 Bericht ueber Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech. 5, 136–139.CrossRefGoogle Scholar
Pullin, D. I., Inoue, M. & Saito, N. 2013 On the asymptotic state of high Reynolds number, smooth-wall turbulent flows. Phys. Fluids 25, 015116.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Townsend, A. A. 1976 Structure of Turbulent Shear Flow, vol. 2. Cambridge University Press.Google Scholar
Tsuji, Y., Lindgren, B. & Johansson, A. V. 2005 Self-similar profile of probability density functions in zero-pressure gradient turbulent boundary layers. Fluid Dyn. Res. 37, 293–316.Google Scholar
Wilczek, M., Daitche, A. & Friedrich, R. 2011 On the velocity distribution in homogeneous isotropic turbulence: correlations and deviations from Gaussianity. J. Fluid Mech. 676, 191–217.Google Scholar