Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T22:45:01.491Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalization of elastohydrodynamic interactions between a rigid sphere and a nearby soft wall

Published online by Cambridge University Press:  30 July 2021

Pratyaksh Karan Open the ORCID record for Pratyaksh Karan [Opens in a new window] ,
Jeevanjyoti Chakraborty Open the ORCID record for Jeevanjyoti Chakraborty [Opens in a new window]  and
Suman Chakraborty Open the ORCID record for Suman Chakraborty [Opens in a new window]
Pratyaksh Karan
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, West Bengal 721302, India
Jeevanjyoti Chakraborty
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, West Bengal 721302, India
Suman Chakraborty*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, West Bengal 721302, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

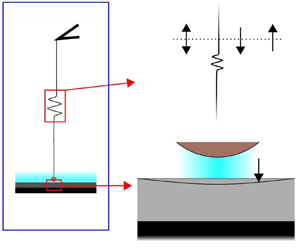
Soft substrates, omnipresent in several fundamental processes ranging from the tribological to biophysical, are often subjected to viscous fluid-mediated dynamic loading for their real-time monitoring, by employing advanced characterization tools in the forms of different surface probing apparatus. Here, we bring out exclusive facets of the two-way interplay between large-amplitude loading of a proximal rigid spherical probe on a soft substrate coating and the combined consequences of electrostatic and van der Waals interactions (modelled as Derjaguin–Landau–Verwey–Overbeek (DVLO) forces) on the same. Our results reveal that for high-frequency oscillatory loading and large amplitude of probe motion, the DLVO interactions do not appreciably affect the force response. On the other hand, for low-frequency high-amplitude oscillatory loading, DLVO effects are shown to magnify the substrate deformation tenfold and the force response by up to two orders of magnitude, in experimentally tractable physical limits. Additionally, we find that compressibility of substrate material increases its deformation by approximately a factor of two. Because of the exact shape of the deformable surface as well as the sphere–substrate separation distance being unknown at every time instant a priori, estimation of the resultant force interactions by simply employing an algebraic linear superposition of the different force components is shown to be inappropriate for characterizing the interactions of a highly compliant substrate in close proximity to the dynamically modulated probe. These results may turn out to be of profound importance in rationalizing the interpretation of surface force measurements on soft substrates in several applications encompassing engineering and nano-bio technology.

JFM classification

Micro-/Nano-fluid dynamics: Microscale transport
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 923 , 25 September 2021 , A32
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anand, V., David, J. & Christov, I.C. 2019 Non-Newtonian fluid–structure interactions: static response of a microchannel due to internal flow of a power-law fluid. J. Non-Newtonian Fluid Mech. 264, 62–72.CrossRefGoogle Scholar
Baddour, N. & Chouinard, U. 2015 Theory and operational rules for the discrete Hankel transform. J. Opt. Soc. Am. 32 (4), 611–622.CrossRefGoogle ScholarPubMed
Bakli, C. & Chakraborty, S. 2012 Capillary filling dynamics of water in nanopores. Appl. Phys. Lett. 101 (15), 153112.CrossRefGoogle Scholar
Bandopadhyay, A. & Chakraborty, S. 2012 a Combined effects of interfacial permittivity variations and finite ionic sizes on streaming potentials in nanochannels. Langmuir 28 (50), 17552–17563.CrossRefGoogle ScholarPubMed
Bandopadhyay, A. & Chakraborty, S. 2012 b Electrokinetically induced alterations in dynamic response of viscoelastic fluids in narrow confinements. Phys. Rev. E 85 (5), 056302.CrossRefGoogle ScholarPubMed
Bandopadhyay, A., Mandal, S., Kishore, N.K. & Chakraborty, S. 2016 Uniform electric-field- induced lateral migration of a sedimenting drop. J. Fluid Mech. 792, 553–589.CrossRefGoogle Scholar
Boyko, E., Eshel, R., Gat, A.D. & Bercovici, M. 2020 Nonuniform electro-osmotic flow drives fluid-structure instability. Phys. Rev. Lett. 124 (2), 024501.CrossRefGoogle ScholarPubMed
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3–4), 242–251.CrossRefGoogle Scholar
Butt, H.-J., Cappella, B. & Kappl, M. 2005 Force measurements with the atomic force microscope: technique, interpretation and applications. Surf. Sci. Rep. 59 (1–6), 1–152.CrossRefGoogle Scholar
Cawthorn, C.J. & Balmforth, N.J. 2010 Contact in a viscous fluid. Part 1. A falling wedge. J. Fluid Mech. 646, 327–338.CrossRefGoogle Scholar
Chadwick, R.S. & Liao, Z. 2008 High-frequency oscillations of a sphere in a viscous fluid near a rigid plane. SIAM Rev. 50 (2), 313–322.CrossRefGoogle Scholar
Chakraborty, J. & Chakraborty, S. 2010 Influence of streaming potential on the elastic response of a compliant microfluidic substrate subjected to dynamic loading. Phys. Fluids 22, 122002.CrossRefGoogle Scholar
Chakraborty, J. & Chakraborty, S. 2011 Combined influence of streaming potential and substrate compliance on load capacity of a planar slider bearing. Phys. Fluids 23 (8), 082004.CrossRefGoogle Scholar
Chakraborty, S. & Durst, F. 2007 Derivations of extended Navier-Stokes equations from upscaled molecular transport considerations for compressible ideal gas flows: towards extended constitutive forms. Phys. Fluids 19 (8), 088104.CrossRefGoogle Scholar
Chakraborty, S. & Padhy, S. 2008 Anomalous electrical conductivity of nanoscale colloidal suspensions. ACS Nano 2 (10), 2029–2036.CrossRefGoogle ScholarPubMed
Chandler, T.G.J. & Vella, D. 2020 Validity of Winkler's mattress model for thin elastomeric layers: beyond Poisson's ratio. Proc. R. Soc. A 476 (2242), 20200551.CrossRefGoogle ScholarPubMed
Christov, I.C., Cognet, V., Shidhore, T.C. & Stone, H.A. 2018 Flow rate–pressure drop relation for deformable shallow microfluidic channels. J. Fluid Mech. 841, 267–286.CrossRefGoogle Scholar
Derjaguin, B. & Landau, L. 1941 The theory of stability of highly charged lyophobic sols and coalescence of highly charged particles in electrolyte solutions. Acta Physicochim. URSS 14, 633–662.Google Scholar
Dey, R., Chakraborty, D. & Chakraborty, S. 2011 Analytical solution for thermally fully developed combined electroosmotic and pressure-driven flows in narrow confinements with thick electrical double layers. J. Heat Transfer 133 (2), 024503.CrossRefGoogle Scholar
Dongari, N., Durst, F. & Chakraborty, S. 2010 Predicting microscale gas flows and rarefaction effects through extended Navier–Stokes–Fourier equations from phoretic transport considerations. Microfluid. Nanofluid. 9 (4–5), 831–846.CrossRefGoogle Scholar
Dowson, D. 1995 Elastohydrodynamic and micro-elastohydrodynamic lubrication. Wear 190 (2), 125–138.CrossRefGoogle Scholar
Ganguly, S. & Chakraborty, S. 2004 Numerical investigation on role of bottom gas stirring in controlling thermal stratification in steel ladles. ISIJ Intl 44 (3), 537–546.CrossRefGoogle Scholar
Gao, S., Liu, B., Peng, J., Zhu, K., Zhao, Y., Li, X. & Yuan, X. 2019 Icephobic durability of branched PDMS slippage coatings co-cross-linked by functionalized POSS. ACS Appl. Mater. Interfaces 11 (4), 4654–4666.CrossRefGoogle ScholarPubMed
Goswami, P. & Chakraborty, S. 2011 Semi-analytical solutions for electroosmotic flows with interfacial slip in microchannels of complex cross-sectional shapes. Microfluid. Nanofluid. 11 (3), 255–267.CrossRefGoogle Scholar
Guan, D., Barraud, C., Charlaix, E. & Tong, P. 2017 Noncontact viscoelastic measurement of polymer thin films in a liquid medium using long-needle atomic force microscopy. Langmuir 33 (6), 1385–1390.CrossRefGoogle Scholar
Harding, J.W. & Sneddon, I.N. 1945 The elastic stresses produced by the indentation of the plane surface of a semi-infinite elastic solid by a rigid punch. Math. Proc. Camb. Phil. Soc. 41 (1), 16–26.CrossRefGoogle Scholar
Higginson, G.R. 1962 A model experiment in elasto-hydrodynamic lubrication. Intl J. Mech. Sci. 4 (3), 205–210.CrossRefGoogle Scholar
Hunter, R.J. 1986 Fundamentals of Colloid Science. Oxford University Press.Google Scholar
Israelachvili, J.N. 2011 Intermolecular and Surface Forces. Academic Press.Google Scholar
Jones, R.E. & Hart, D.P. 2005 Force interactions between substrates and SPM cantilevers immersed in fluids. Tribol. Intl 38 (3), 355–361.CrossRefGoogle Scholar
Kar, S., Maiti, T.K. & Chakraborty, S. 2015 Capillarity-driven blood plasma separation on paper-based devices. Analyst 140 (19), 6473–6476.CrossRefGoogle ScholarPubMed
Karan, P., Chakraborty, J. & Chakraborty, S. 2018 Electrokinetics over hydrophobic surfaces. Electrophoresis 40a, 616–624.Google Scholar
Karan, P., Chakraborty, J. & Chakraborty, S. 2018 b Small-scale flow with deformable boundaries. J. Indian Inst. Sci. 98 (2), 159–183.CrossRefGoogle Scholar
Karan, P., Chakraborty, J. & Chakraborty, S. 2020 a Influence of non-hydrodynamic forces on the elastic response of an ultra-thin soft coating under fluid-mediated dynamic loading. Phys. Fluids 32 (2), 022002.CrossRefGoogle Scholar
Karan, P., Chakraborty, J., Chakraborty, S., Wereley, S.T. & Christov, I.C. 2020 b Profiling a soft solid layer to passively control the conduit shape in a compliant microchannel during flow. arXiv:2012.03887.CrossRefGoogle Scholar
Karan, P., Das, S.S., Mukherjee, R., Chakraborty, J. & Chakraborty, S. 2020 c Flow and deformation characteristics of a flexible microfluidic channel with axial gradients in wall elasticity. Soft Matt. 16, 5777–5786.CrossRefGoogle ScholarPubMed
Leroy, S. & Charlaix, É. 2011 Hydrodynamic interactions for the measurement of thin film elastic properties. J. Fluid Mech. 674, 389–407.CrossRefGoogle Scholar
Leroy, S., Steinberger, A., Cottin-Bizonne, C., Restagno, F., Léger, L. & Charlaix, É. 2012 Hydrodynamic interaction between a spherical particle and an elastic surface: A gentle probe for soft thin films. Phys. Rev. Lett. 108, 264501.CrossRefGoogle Scholar
Mukherjee, U., Chakraborty, J. & Chakraborty, S. 2013 Relaxation characteristics of a compliant microfluidic channel under electroosmotic flow. Soft Matt. 9 (5), 1562–1569.CrossRefGoogle Scholar
Müller, D.J, Fotiadis, D., Scheuring, S., Müller, S.A. & Engel, A. 1999 Electrostatically balanced subnanometer imaging of biological specimens by atomic force microscope. Biophys. J. 76 (2), 1101–1111.CrossRefGoogle ScholarPubMed
Naik, K.G., Chakraborty, S. & Chakraborty, J. 2017 Finite size effects of ionic species sensitively determine load bearing capacities of lubricated systems under combined influence of electrokinetics and surface compliance. Soft Matt. 13, 6422–6429.CrossRefGoogle ScholarPubMed
Ostromohov, N., Rofman, B., Bercovici, M. & Kaigala, G. 2020 Electrokinetic scanning probe. Small 16 (5), 1904268.CrossRefGoogle ScholarPubMed
Pandey, A., Karpitschka, S., Venner, C.H. & Snoeijer, J.H. 2016 Lubrication of soft viscoelastic solids. J. Fluid Mech. 799, 433–447.CrossRefGoogle Scholar
Peach, M.S., et al. 2012 Design and optimization of polyphosphazene functionalized fiber matrices for soft tissue regeneration. J. Biomed. Nanotechnol. 8 (1), 107–124.CrossRefGoogle ScholarPubMed
Phan-Thien, N. & Mai-Duy, N. 2017 Understanding Viscoelasticity: An Introduction To Rheology. Springer.CrossRefGoogle Scholar
Priyadarshani, J., Awasthi, P., Karan, P., Das, S. & Chakraborty, S. 2021 Transport of vascular endothelial growth factor dictates on-chip angiogenesis in tumor microenvironment. Phys. Fluids 33, 031910.CrossRefGoogle Scholar
Quesson, B.A.J, Vanneer, P.L.M.J., Vanrie, M.C.J.M., Vanes, M.H., Piras, D., Hatakeyama, K., Mohtashami, A., Navarro, V., Duivcnvoorde, T. & Sadeghian, H. 2018 Efficient and stable acoustical coupling for GHz subsurface probe microscopy. In 2018 IEEE International Ultrasonics Symposium (IUS), pp. 1–4. IEEE.CrossRefGoogle Scholar
Radmacher, M., Cleveland, J.P., Fritz, M., Hansma, H.G. & Hansma, P.K. 1994 Mapping interaction forces with the atomic force microscope. Biophys. J. 66 (6), 2159–2165.CrossRefGoogle ScholarPubMed
Rallabandi, B., Saintyves, B., Jules, T., Salez, T., Schönecker, C., Mahadevan, L. & Stone, H.A. 2017 Rotation of an immersed cylinder sliding near a thin elastic coating. Phys. Rev. Fluids 2 (7), 074102.CrossRefGoogle Scholar
Rubin, S., Tulchinsky, A., Gat, A.D. & Bercovici, M. 2017 Elastic deformations driven by non-uniform lubrication flows. J. Fluid Mech. 812, 841–865.CrossRefGoogle Scholar
Scaraggi, M. & Persson, B.N.J. 2014 Theory of viscoelastic lubrication. Tribol. Intl 72, 118–130.CrossRefGoogle Scholar
Secomb, T.W., Skalak, R., Özkaya, N. & Gross, J.F. 1986 Flow of axisymmetric red blood cells in narrow capillaries. J. Fluid Mech. 163, 405–423.CrossRefGoogle Scholar
Serayssol, J. & Davis, R.H. 1986 The influence of surface interactions on the elastohydrodynamic collision of two spheres. J. Colloid Interface Sci. 114, 54–66.CrossRefGoogle Scholar
Shekhawat, G.S., Srivastava, A.K., Dravid, V.P. & Balogun, O. 2017 Thickness resonance acoustic microscopy for nanomechanical subsurface imaging. ACS Nano 11 (6), 6139–6145.CrossRefGoogle ScholarPubMed
Shubin, V.E. & Kékicheff, P. 1993 Electrical double layer structure revisited via a surface force apparatus: mica interfaces in lithium nitrate solutions. J. Colloid Interface Sci. 155 (1), 108–123.CrossRefGoogle Scholar
Silkina, E.F., Asmolov, E.S. & Vinogradova, O.I. 2019 Electro-osmotic flow in hydrophobic nanochannels. Phys. Chem. Chem. Phys. 21 (41), 23036–23043.CrossRefGoogle ScholarPubMed
Skotheim, J.M. & Mahadevan, L. 2004 Soft lubrication. Phys. Rev. Lett. 92 (24), 245509.CrossRefGoogle ScholarPubMed
Skotheim, J.M. & Mahadevan, L. 2005 Soft lubrication: the elastohydrodynamics of nonconforming and conforming contacts. Phys. Fluids 17, 092101.CrossRefGoogle Scholar
Steinberger, A., Cottin-Bizonne, C., Kleimann, P. & Charlaix, E. 2008 Nanoscale flow on a bubble mattress: effect of surface elasticity. Phys. Rev. Lett. 100 (13), 134501.CrossRefGoogle ScholarPubMed
Sunil, G.B., Agarwal, A., Karan, P., Chakraborty, J. & Chakraborty, S. 2020 Deformation behaviour of viscoelastic microchannel with axially graded wall softness. In Proceedings of the 8th International and 47th National Conference on Fluid Mechanics and Fluid Power (FMFP), p. FMFP2020-035 (1–6). NSFMFP.Google Scholar
Tabatabaei, S.M., van de Ven, T.G.M. & Rey, A.D. 2006 Electroviscous sphere–wall interactions. J. Colloid Interface Sci. 301 (1), 291–301.CrossRefGoogle ScholarPubMed
Talapatra, S. & Chakraborty, S. 2008 Double layer overlap in ac electroosmosis. Eur. J. Mech. B/Fluids 27 (3), 297–308.CrossRefGoogle Scholar
Tan, M.R., Wang, Y. & Frechette, J. 2019 Criterion for particle rebound during wet collisions on elastic coatings. Phys. Rev. Fluids 4 (8), 084305.CrossRefGoogle Scholar
Temizer, I. & Stupkiewicz, S. 2016 Formulation of the Reynolds equation on a time-dependent lubrication surface. Proc. R. Soc. A 472 (2187), 20160032.CrossRefGoogle ScholarPubMed
Trouilloud, R., Yu, T.S., Hosoi, A.E. & Lauga, E. 2008 Soft swimming: exploiting deformable interfaces for low Reynolds number locomotion. Phys. Rev. Lett. 101 (4), 048102.CrossRefGoogle ScholarPubMed
Urzay, J. 2010 Asymptotic theory of the elastohydrodynamic adhesion and gliding motion of a solid particle over soft and sticky substrates at low Reynolds numbers. J. Fluid Mech. 653, 391–429.CrossRefGoogle Scholar
Urzay, J., Smith, S.G.L. & Glover, B.J. 2007 The elastohydrodynamic force on a sphere near a soft wall. Phys. Fluids 19, 103106.CrossRefGoogle Scholar
Verwey, E.J.W. 1947 Theory of the stability of lyophobic colloids. J. Phys. Chem. 51 (3), 631–636.CrossRefGoogle ScholarPubMed
Vinogradova, O.I. & Feuillebois, F. 2000 Elastohydrodynamic collision of two spheres allowing slip on their surfaces. J. Colloid Interface Sci. 221 (1), 1–12.CrossRefGoogle ScholarPubMed
Wang, X. & Christov, I.C. 2019 Theory of the flow-induced deformation of shallow compliant microchannels with thick walls. Proc. R. Soc. A 475 (2231), 20190513.CrossRefGoogle ScholarPubMed
Wang, Y., Dhong, C. & Frechette, J. 2015 Out-of-contact elastohydrodynamic deformation due to lubrication forces. Phys. Rev. Lett. 115 (24), 248302.CrossRefGoogle ScholarPubMed
Wang, Y., Tan, M.R. & Frechette, J. 2017 Elastic deformation of soft coatings due to lubrication forces. Soft Matt. 13 (38), 6718–6729.CrossRefGoogle ScholarPubMed
Yavari, H., Sadeghi, A., Saidi, M.H. & Chakraborty, S. 2012 Combined influences of viscous dissipation, non-uniform joule heating and variable thermophysical properties on convective heat transfer in microtubes. Intl J. Heat Mass Transfer 55 (4), 762–772.CrossRefGoogle Scholar
Zhang, C. 2005 Research on thin film lubrication: state of the art. Tribol. Intl 38 (4), 443–448.CrossRefGoogle Scholar
Zhang, Z., Bertin, V., Arshad, M., Raphael, E., Salez, T. & Maali, A. 2020 Direct measurement of the elastohydrodynamic lift force at the nanoscale. Phys. Rev. Lett. 124 (5), 054502.Google Scholar
Zhao, C., Zhang, W., van den Ende, D. & Mugele, F. 2020 Electroviscous effects on the squeezing flow of thin electrolyte solution films. J. Fluid Mech. 888, A29.CrossRefGoogle Scholar
Zhao, Z., Ukidve, A., Krishnan, V. & Mitragotri, S. 2019 Effect of physicochemical and surface properties on in vivo fate of drug nanocarriers. Adv. Drug Deliv. Rev. 143, 3–21.CrossRefGoogle ScholarPubMed
Supplementary material: File

Karan et al. supplementary material

Karan et al. supplementary material

Download Karan et al. supplementary material(File)
File 27.2 MB